Number series generator challenge solutions – Part 5

This is the fifth and last part in the series covering solutions to the number series generator challenge. In Part 1, Part 2, Part 3 and Part 4 I covered pure T-SQL solutions. Early on when I posted the puzzle, several people commented that the best performing solution would likely be a CLR-based one. In this article we’ll put this intuitive assumption to the test. Specifically, I’ll cover CLR-based solutions posted by Kamil Kosno and Adam Machanic.

Many thanks to Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea, and Paul White for sharing your ideas and comments.

I’ll do my testing in a database called testdb. Use the following code to create the database if it doesn’t exist, and to enable I/O and time statistics:

-- DB and stats
SET NOCOUNT ON;
SET STATISTICS IO, TIME ON;
GO

IF DB_ID('testdb') IS NULL CREATE DATABASE testdb;
GO

USE testdb;
GO

For simplicity’s sake, I’ll disable CLR strict security and make the database trustworthy using the following code:

-- Enable CLR, disable CLR strict security and make db trustworthy
EXEC sys.sp_configure 'show advanced settings', 1;
RECONFIGURE;

EXEC sys.sp_configure 'clr enabled', 1;
EXEC sys.sp_configure 'clr strict security', 0;
RECONFIGURE;

EXEC sys.sp_configure 'show advanced settings', 0;
RECONFIGURE;

ALTER DATABASE testdb SET TRUSTWORTHY ON; 
GO

Earlier solutions

Before I cover the CLR-based solutions, let’s quickly review the performance of two of the best performing T-SQL solutions.

The best performing T-SQL solution that didn’t use any persisted base tables (other than the dummy empty columnstore table to get batch processing), and therefore involved no I/O operations, was the one implemented in the function dbo.GetNumsAlanCharlieItzikBatch. I covered this solution in Part 1.

Here’s the code to create the dummy empty columnstore table that the function’s query uses:

DROP TABLE IF EXISTS dbo.BatchMe;
GO

CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
GO

And here’s the code with the function’s definition:

CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  WITH
    L0 AS ( SELECT 1 AS c
            FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
                        (1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
    L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
    L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
    L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
    Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
              FROM L3 )
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
     @low - 1 + rownum AS n
  FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
  ORDER BY rownum;
GO

Let’s first test the function requesting a series of 100M numbers, with the MAX aggregate applied to column n:

SELECT MAX(n) AS mx FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

Recall, this testing technique avoids transmitting 100M rows to the caller, and also avoids the row-mode effort involved in variable assignment when using the variable assignment technique.

Here are the time stats that I got for this test on my machine:

The execution of this function doesn’t produce any logical reads, of course.

Next, let’s test it with order, using the variable assignment technique:

DECLARE @n AS BIGINT;

SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) ORDER BY n OPTION(MAXDOP 1);

I got the following time stats for this execution:

Recall that this function doesn’t result in sorting when requesting the data ordered by n; you basically get the same plan whether you request the data ordered or not. We can attribute most of the extra time in this test compared to the previous one to the 100M row-mode based variable assignments.

The best performing T-SQL solution that did use a persisted base table, and therefore resulted in some I/O operations, though very few, was Paul White’s solution implemented in the function dbo.GetNums_SQLkiwi. I covered this solution in Part 4.

Here’s Paul’s code to create both the columnstore table used by the function and the function itself:

-- Helper columnstore table
DROP TABLE IF EXISTS dbo.CS;
 
-- 64K rows (enough for 4B rows when cross joined)
-- column 1 is always zero
-- column 2 is (1...65536)
SELECT
    -- type as integer NOT NULL
    -- (everything is normalized to 64 bits in columnstore/batch mode anyway)
    n1 = ISNULL(CONVERT(integer, 0), 0), 
    n2 = ISNULL(CONVERT(integer, N.rn), 0)
INTO dbo.CS
FROM 
(
    SELECT
        rn = ROW_NUMBER() OVER (ORDER BY @@SPID)
    FROM master.dbo.spt_values AS SV1
    CROSS JOIN master.dbo.spt_values AS SV2
    ORDER BY 
        rn ASC
        OFFSET 0 ROWS
        FETCH NEXT 65536 ROWS ONLY
) AS N;

-- Single compressed rowgroup of 65,536 rows
CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS 
WITH (MAXDOP = 1);
GO

-- The function
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scalar
        @low - 2 + N.rn < @high;
GO

Let’s first test it without order using the aggregate technique, resulting in an all-batch-mode-plan:

SELECT MAX(n) AS mx FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(MAXDOP 1);

I got the following time and I/O stats for this execution:

Let’s test the function with order using the variable assignment technique:

DECLARE @n AS BIGINT;

SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000) ORDER BY n OPTION(MAXDOP 1);

Like with the previous solution, also this solution avoids explicit sorting in the plan, and therefore gets the same plan whether you ask for the data ordered or not. But again, this test incurs an extra penalty mainly due to the variable assignment technique used here, resulting in the variable assignment part in the plan getting processed in row mode.

Here are the time and I/O stats that I got for this execution:

CLR Solutions

Both Kamil Kosno and Adam Machanic first provided a simple CLR-only solution, and later came up with a more sophisticated CLR+T-SQL combo. I’ll start with Kamil’s solutions and then cover Adam’s solutions.

Solutions by Kamil Kosno

Here’s the CLR code used in Kamil’s first solution to define a function called GetNums_KamilKosno1:

using System;
using System.Data.SqlTypes;
using System.Collections;
public partial class GetNumsKamil1
{
    [Microsoft.SqlServer.Server.SqlFunction(FillRowMethodName = "GetNums_KamilKosno1_Fill", TableDefinition = "n BIGINT")]
    public static IEnumerator GetNums_KamilKosno1(SqlInt64 low, SqlInt64 high)
    {
        return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0) : new GetNumsCS(low.Value, high.Value);
    }

    public static void GetNums_KamilKosno1_Fill(Object o, out SqlInt64 n)
    {
        n = (long)o;
    }

    private class GetNumsCS : IEnumerator
    {
        public GetNumsCS(long from, long to)
        {
            _lowrange = from;
            _current = _lowrange - 1;
            _highrange = to;
        }

        public bool MoveNext()
        {
            _current += 1;
            if (_current > _highrange) return false;
            else return true;
        }

        public object Current
        {
            get
            {

                return _current;
            }
        }
        
        public void Reset()
        {
            _current = _lowrange - 1;
        }

        long _lowrange;
        long _current;
        long _highrange;
    }
}

The function accepts two inputs called low and high and returns a table with a BIGINT column called n. The function is a streaming kind, returning a row with the next number in the series per row request from the calling query. As you can see, Kamil chose the more formalized method of implementing the IEnumerator interface, which involves implementing the methods MoveNext (advances the enumerator to get the next row), Current (gets the row in the current enumerator position), and Reset (sets the enumerator to its initial position, which is before the first row).

The variable holding the current number in the series is called _current. The constructor sets _current to the low bound of the requested range minus 1, and same goes for the Reset method. The MoveNext method advances _current by 1. Then, if _current is greater than the high bound of the requested range, the method returns false, meaning it won’t be called again. Otherwise, it returns true, meaning it will be called again. The method Current naturally returns _current. As you can see, pretty basic logic.

I called the Visual Studio project GetNumsKamil1, and used the path C:\Temp\ for it. Here’s the code I used to deploy the function in the testdb database:

DROP FUNCTION IF EXISTS dbo.GetNums_KamilKosno1;

DROP ASSEMBLY IF EXISTS GetNumsKamil1;
GO

CREATE ASSEMBLY GetNumsKamil1
  FROM 'C:\Temp\GetNumsKamil1\GetNumsKamil1\bin\Debug\GetNumsKamil1.dll';
GO

CREATE FUNCTION dbo.GetNums_KamilKosno1(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE(n BIGINT)
  ORDER(n)
  AS EXTERNAL NAME GetNumsKamil1.GetNumsKamil1.GetNums_KamilKosno1;
GO

Notice the use of the ORDER clause in the CREATE FUNCTION statement. The function emits the rows in n ordering, so when the rows need to be ingested in the plan in n ordering, based on this clause SQL Server knows that it can avoid a sort in the plan.

Let’s test the function, first with the aggregate technique, when ordering is not needed:

SELECT MAX(n) AS mx FROM dbo.GetNums_KamilKosno1(1, 100000000);

I got the plan shown in Figure 1.

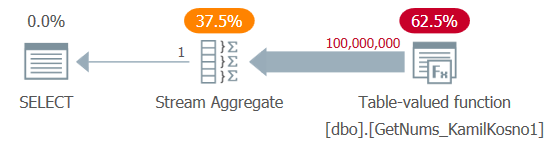Figure 1: Plan for dbo.GetNums_KamilKosno1 function

There’s not much to say about this plan, other than the fact that all operators use row execution mode.

I got the following time stats for this execution:

And of course, no logical reads were involved.

Let’s test the function with order, using the variable assignment technique:

DECLARE @n AS BIGINT;

SELECT @n = n FROM dbo.GetNums_KamilKosno1(1, 100000000) ORDER BY n;

I got the plan shown in Figure 2 for this execution.

Figure 2: Plan for dbo.GetNums_KamilKosno1 function with ORDER BY

Notice that there’s no sorting in the plan since the function was created with the ORDER(n) clause. However, there is some effort in ensuring that the rows are indeed emitted from the function in the promised order. This is done using the Segment and Sequence Project operators, which are used to compute row numbers, and the Assert operator, which aborts the query execution if the test fails. This work has linear scaling—unlike the n log n scaling you would have gotten had a sort been required—but it’s still not cheap. I got the following time stats for this test:

The results could be surprising to some—especially those who intuitively assumed that the CLR-based solutions would perform better than the T-SQL ones. As you can see, the execution times are an order of magnitude longer than with our best performing T-SQL solution.

Kamil’s second solution is a CLR-T-SQL hybrid. Beyond the low and high inputs, the CLR function (GetNums_KamilKosno2) adds a step input, and returns values between low and high that are step apart from each other. Here’s the CLR code Kamil used in his second solution:

using System;
using System.Data.SqlTypes;
using System.Collections;

public partial class GetNumsKamil2
{
    [Microsoft.SqlServer.Server.SqlFunction(DataAccess = Microsoft.SqlServer.Server.DataAccessKind.None, IsDeterministic = true, IsPrecise = true, FillRowMethodName = "GetNums_Fill", TableDefinition = "n BIGINT")]

    public static IEnumerator GetNums_KamilKosno2(SqlInt64 low, SqlInt64 high, SqlInt64 step)
    {
        return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0, step.Value) : new GetNumsCS(low.Value, high.Value, step.Value);
    }

    public static void GetNums_Fill(Object o, out SqlInt64 n)
    {
        n = (long)o;
    }

    private class GetNumsCS : IEnumerator
    {
        public GetNumsCS(long from, long to, long step)
        {
            _lowrange = from;
            _step = step;
            _current = _lowrange - _step;
            _highrange = to;
        }
        
        public bool MoveNext()
        {
            _current = _current + _step;
            if (_current > _highrange) return false;
            else return true;
        }

        public object Current
        {
            get
            {
                return _current;
            }
        }
        
        public void Reset()
        {
            _current = _lowrange - _step;
        }

        long _lowrange;
        long _current;
        long _highrange;
        long _step;
    }
}

I named the VS project GetNumsKamil2, placed it in the path C:\Temp\ too, and used the following code to deploy it in the testdb database:

-- Create assembly and function
DROP FUNCTION IF EXISTS dbo.GetNums_KamilKosno2;
DROP ASSEMBLY IF EXISTS GetNumsKamil2;
GO

CREATE ASSEMBLY GetNumsKamil2
  FROM 'C:\Temp\GetNumsKamil2\GetNumsKamil2\bin\Debug\GetNumsKamil2.dll';
GO

CREATE FUNCTION dbo.GetNums_KamilKosno2
    (@low AS BIGINT = 1, @high AS BIGINT, @step AS BIGINT)
  RETURNS TABLE(n BIGINT)
  ORDER(n)
  AS EXTERNAL NAME GetNumsKamil2.GetNumsKamil2.GetNums_KamilKosno2;
GO

As an example for using the function, here’s a request to generate values between 5 and 59, with a step of 10:

SELECT n FROM dbo.GetNums_KamilKosno2(5, 59, 10);

This code generates the following output:

n
---
5
15
25
35
45
55

As for the T-SQL part, Kamil used a function called dbo.GetNums_Hybrid_Kamil2, with the following code:

CREATE OR ALTER FUNCTION dbo.GetNums_Hybrid_Kamil2(@low AS BIGINT, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  SELECT TOP (@high - @low + 1) V.n
  FROM dbo.GetNums_KamilKosno2(@low, @high, 10) AS GN
    CROSS APPLY (VALUES(0+GN.n),(1+GN.n),(2+GN.n),(3+GN.n),(4+GN.n),
                       (5+GN.n),(6+GN.n),(7+GN.n),(8+GN.n),(9+GN.n)) AS V(n);
GO

As you can see, the T-SQL function invokes the CLR function with the same @low and @high inputs that it gets, and in this example uses a step size of 10. The query uses CROSS APPLY between the CLR function’s result and a table -value constructor that generates the final numbers by adding values in the range 0 through 9 to the beginning of the step. The TOP filter is used to ensure that you don’t get more than the number of numbers you requested.

Important: I should stress that Kamil makes an assumption here about the TOP filter being applied based on the result number ordering, which is not really guaranteed since the query doesn’t have an ORDER BY clause. If you either add an ORDER BY clause to support TOP, or substitute TOP with a WHERE filter, to guarantee a deterministic filter, this could completely change the performance profile of the solution.

At any rate, let’s first test the function without order using the aggregate technique:

SELECT MAX(n) AS mx FROM dbo.GetNums_Hybrid_Kamil2(1, 100000000);

I got the plan shown in Figure 3 for this execution.

Figure 3: Plan for dbo.GetNums_Hybrid_Kamil2 function

Again, all operators in the plan use row execution mode.

I got the following time stats for this execution:

And naturally no logical reads.

Let’s test the function with order:

DECLARE @n AS BIGINT;

SELECT @n = n FROM dbo.GetNums_Hybrid_Kamil2(1, 100000000) ORDER BY n;

I got the plan shown in in Figure 4.

Figure 4: Plan for dbo.GetNums_Hybrid_Kamil2 function with ORDER BY

Since the result numbers are the outcome of manipulation of the low bound of the step returned by the CLR function and the delta added in the table-value constructor, the optimizer doesn’t trust that the result numbers are generated in the requested order, and adds explicit sorting to the plan.

I got the following time stats for this execution:

So it seems that when no order is needed, Kamil’s second solution does better than his first. But when order is needed, it’s the other way around. Either way, the T-SQL solutions are faster. Personally, I’d trust the correctness of the first solution, but not the second.

Solutions by Adam Machanic

Adam’s first solution is also a basic CLR function that keeps incrementing a counter. Only instead of using the more involved formalized approach like Kamil did, Adam used a simpler approach that invokes the yield command per row that needs to be returned.

Here’s Adam’s CLR code for his first solution, defining a streaming function called GetNums_AdamMachanic1:

using System.Data.SqlTypes;
using System.Collections;

public partial class GetNumsAdam1
{
    [Microsoft.SqlServer.Server.SqlFunction(
        FillRowMethodName = "GetNums_AdamMachanic1_fill",
        TableDefinition = "n BIGINT")]
        
    public static IEnumerable GetNums_AdamMachanic1(SqlInt64 min, SqlInt64 max)
    {
        var min_int = min.Value;
        var max_int = max.Value;
        for (; min_int <= max_int; min_int++)
        {
            yield return (min_int);
        }
    }

    public static void GetNums_AdamMachanic1_fill(object o, out long i)
    {
        i = (long)o;
    }
};

The solution is so elegant in its simplicity. As you can see, the function accepts two inputs called min and max representing the low and high boundary points of the requested range, and returns a table with a BIGINT column called n. The function initializes variables called min_int and max_int with the respective function’s input parameter values. The function then runs a loop as long as min_int <= max_int, that in each iteration yields a row with the current value of min_int and increments min_int by 1. That’s it.

I named the project GetNumsAdam1 in VS, placed it in C:\Temp\, and used the following code to deploy it:

-- Create assembly and function
DROP FUNCTION IF EXISTS dbo.GetNums_AdamMachanic1;
DROP ASSEMBLY IF EXISTS GetNumsAdam1;
GO

CREATE ASSEMBLY GetNumsAdam1
  FROM 'C:\Temp\GetNumsAdam1\GetNumsAdam1\bin\Debug\GetNumsAdam1.dll';
GO

CREATE FUNCTION dbo.GetNums_AdamMachanic1(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE(n BIGINT)
  ORDER(n)
  AS EXTERNAL NAME GetNumsAdam1.GetNumsAdam1.GetNums_AdamMachanic1;
GO

I used the following code to test it with the aggregate technique, for cases when order doesn’t matter:

SELECT MAX(n) AS mx FROM dbo.GetNums_AdamMachanic1(1, 100000000);

I got the plan shown in Figure 5 for this execution.

Figure 5: Plan for dbo.GetNums_AdamMachanic1 function

The plan is very similar to the plan you saw earlier for Kamil’s first solution, and the same applies to its performance. I got the following time stats for this execution:

And of course no logical reads were needed.

Let’s test the function with order, using the variable assignment technique:

DECLARE @n AS BIGINT;

SELECT @n = n FROM dbo.GetNums_AdamMachanic1(1, 100000000) ORDER BY n;

I got the plan shown in Figure 6 for this execution.

Figure 6: Plan for dbo.GetNums_AdamMachanic1 function with ORDER BY

Again, the plan looks similar to the one you saw earlier for Kamil’s first solution. There was no need for explicit sorting since the function was created with the ORDER clause, but the plan does include some work to verify that the rows are indeed returned ordered as promised.

I got the following time stats for this execution:

In his second solution, Adam also combined a CLR part and a T-SQL part. Here’s Adam’s description of the logic he used in his solution:

The logic seems pretty straightforward.

Here’s the code used to define the CLR function called GetNums_AdamMachanic2_8192_base:

using System.Data.SqlTypes;
using System.Collections;

public partial class GetNumsAdam2
{
    private struct row
    {
        public long max_base;
        public long base_add;
    }

    [Microsoft.SqlServer.Server.SqlFunction(
        FillRowMethodName = "GetNums_AdamMachanic2_8192_base_fill",
        TableDefinition = "max_base int, base_add int")]

    public static IEnumerable GetNums_AdamMachanic2_8192_base(SqlInt64 min, SqlInt64 max)
    {
        var min_int = min.Value;
        var max_int = max.Value;
        var min_group = min_int / 8192;
        var max_group = max_int / 8192;
        
        for (; min_group <= max_group; min_group++)
        {
            if (min_int > max_int)
                yield break;
            var max_base = 8192 - (min_int % 8192);
            if (min_group == max_group && max_int < (((max_int / 8192) + 1) * 8192) - 1)
                max_base = max_int - min_int + 1;
            yield return (
                new row()
                {
                    max_base = max_base,
                    base_add = min_int
                }
            );
            min_int = (min_group + 1) * 8192;
        }
    }

    public static void GetNums_AdamMachanic2_8192_base_fill(object o, out long max_base, out long base_add)
    {
        var r = (row)o;
        max_base = r.max_base;
        base_add = r.base_add;
    }
};

I named the VS project GetNumsAdam2 and placed in in the path C:\Temp\ like with the other projects. Here’s the code I used to deploy the function in the testdb database:

-- Create assembly and function
DROP FUNCTION IF EXISTS dbo.GetNums_AdamMachanic2_8192_base;
DROP ASSEMBLY IF EXISTS GetNumsAdam2;
GO

CREATE ASSEMBLY GetNumsAdam2
  FROM 'C:\Temp\GetNumsAdam2\GetNumsAdam2\bin\Debug\GetNumsAdam2.dll';
GO

CREATE FUNCTION dbo.GetNums_AdamMachanic2_8192_base(@max_base AS BIGINT, @add_base AS BIGINT)
  RETURNS TABLE(max_base BIGINT, base_add BIGINT)
  ORDER(base_add)
  AS EXTERNAL NAME GetNumsAdam2.GetNumsAdam2.GetNums_AdamMachanic2_8192_base;
GO

Here’s an example for using GetNums_AdamMachanic2_8192_base with the range 1 through 100M:

SELECT * FROM dbo.GetNums_AdamMachanic2_8192_base(1, 100000000);

This code generates the following output, shown here in abbreviated form:

max_base             base_add
-------------------- --------------------
8191                 1
8192                 8192
8192                 16384
8192                 24576
8192                 32768
...
8192                 99966976
8192                 99975168
8192                 99983360
8192                 99991552
257                  99999744

(12208 rows affected)

Here’s the code with the definition of the T-SQL function GetNums_AdamMachanic2_8192 (abbreviated):

CREATE OR ALTER FUNCTION dbo.GetNums_AdamMachanic2_8192(@max_base AS BIGINT, @add_base AS BIGINT)
  RETURNS TABLE
AS
RETURN
  SELECT TOP (@max_base) V.i + @add_base AS val
  FROM (
    VALUES
    (0),
    (1),
    (2),
    (3),
    (4),
    ...
    (8187),
    (8188),
    (8189),
    (8190),
    (8191)
  ) AS V(i);
GO

Important: Also here, I should stress that similar to what I said about Kamil’s second solution, Adam makes an assumption here that the TOP filter will extract the top rows based on row appearance order in the table-value constructor, which is not really guaranteed. If you add an ORDER BY clause to support TOP or change the filter to a WHERE filter, you’ll get a deterministic filter, but this can completely change the performance profile of the solution.

Finally, here’s the outermost T-SQL function, dbo.GetNums_AdamMachanic2, which the end user calls to get the number series:

CREATE OR ALTER FUNCTION dbo.GetNums_AdamMachanic2(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  SELECT Y.val AS n
  FROM ( SELECT max_base, base_add
  	     FROM dbo.GetNums_AdamMachanic2_8192_base(@low, @high) ) AS X
    CROSS APPLY dbo.GetNums_AdamMachanic2_8192(X.max_base, X.base_add) AS Y
GO

This function uses the CROSS APPLY operator to apply the inner T-SQL function dbo.GetNums_AdamMachanic2_8192 per row returned by the inner CLR function dbo.GetNums_AdamMachanic2_8192_base.

Let’s first test this solution using the aggregate technique when order doesn’t matter:

SELECT MAX(n) AS mx FROM dbo.GetNums_AdamMachanic2(1, 100000000);

I got the plan shown in Figure 7 for this execution.

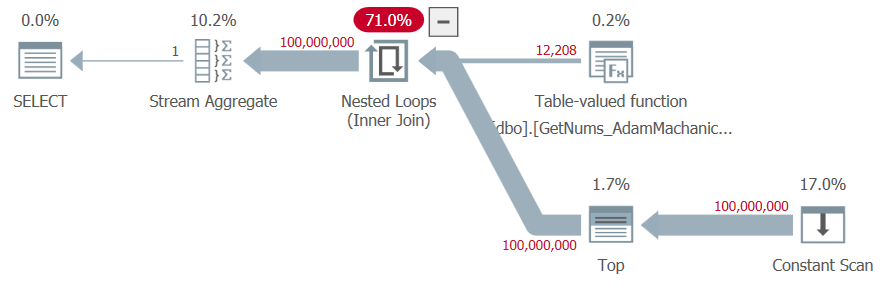Figure 7: Plan for dbo.GetNums_AdamMachanic2 function

I got the following time stats for this test:

No logical reads were needed.

The execution time is not bad, but notice the high compile time due to the large table-value constructor used. You would pay such high compile time irrespective of the range size that you request, so this is especially tricky when using the function with very small ranges. And this solution is still slower than the T-SQL ones.

Let’s test the function with order:

DECLARE @n AS BIGINT;

SELECT @n = n FROM dbo.GetNums_AdamMachanic2(1, 100000000) ORDER BY n;

I got the plan shown in Figure 8 for this execution.

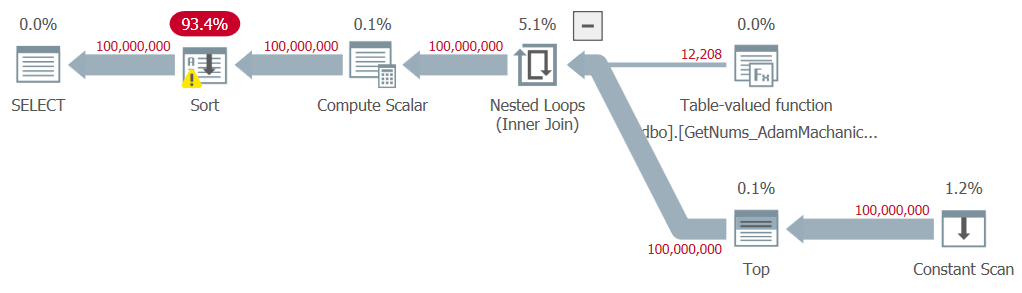Figure 8: Plan for dbo.GetNums_AdamMachanic2 function with ORDER BY

Like with Kamil’s second solution, an explicit sort is needed in the plan, casing a significant performance penalty. Here are the time stats that I got for this test:

Plus, there’s still the high compile time penalty of about a third of a second.

Conclusion

It was interesting to test CLR-based solutions to the number series challenge because many people initially assumed that the best performing solution will likely be a CLR-based one. Kamil and Adam used similar approaches, with the first attempt using a simple loop that increments a counter and yields a row with the next value per iteration, and the more sophisticated second attempt that combines CLR and T-SQL parts. Personally, I don’t feel comfortable with the fact that in both Kamil’s and Adam’s second solutions they relied on a nondeterministic TOP filter, and when I converted it to a deterministic one in my own testing, it had an adverse impact on the solution’s performance. Either way, our two T-SQL solutions perform better than the CLR ones, and do not result in explicit sorting in the plan when you need the rows ordered. So I don’t really see the value in pursuing the CLR route any further. Figure 9 has a performance summary of the solutions that I presented in this article.

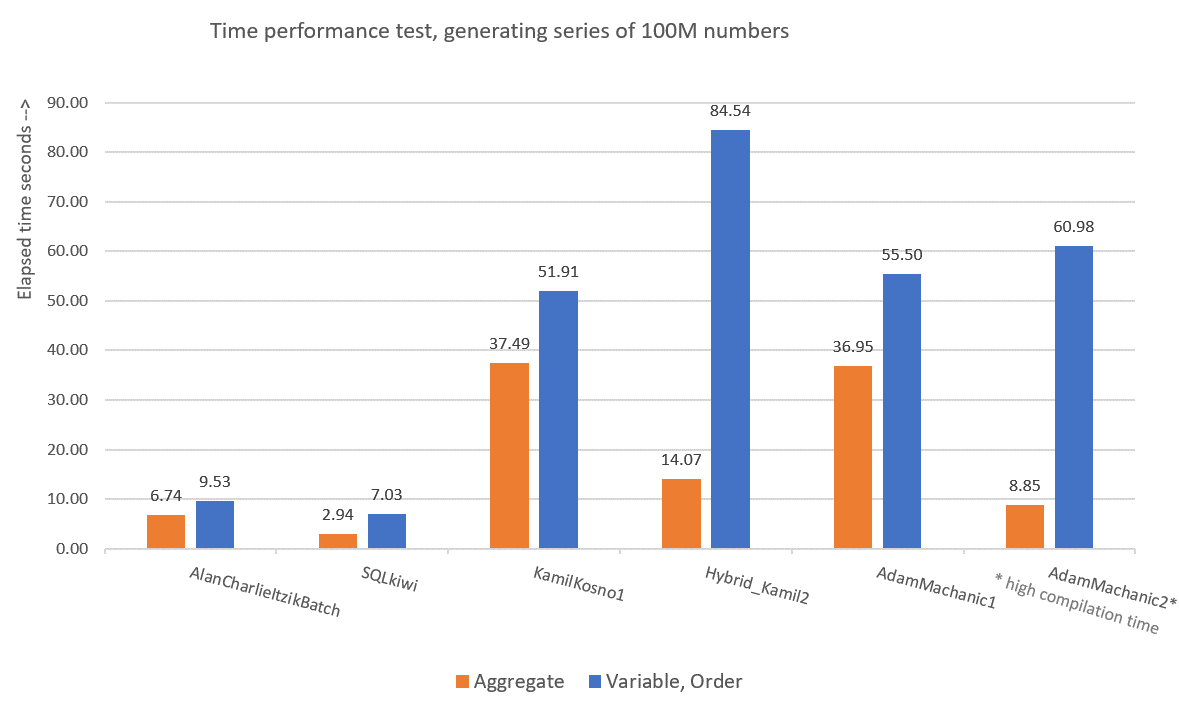Figure 9: Time performance comparison

To me, GetNums_AlanCharlieItzikBatch should be the solution of choice when you require absolutely no I/O footprint, and GetNums_SQKWiki should be preferred when you don’t mind a small I/O footprint. Of course, we can always hope that one day Microsoft will add this critically useful tool as a built-in one, and hopefully if/when they do, it will be a performant solution that supports batch processing and parallelism. So don’t forget to vote for this feature improvement request, and maybe even add your comments for why it’s important for you.

I really enjoyed working on this series. I learned a lot during the process, and hope that you did too.