In Part 5 of my series on table expressions I provided the following solution for generating a series of numbers using CTEs, a table value constructor and cross joins:
DECLARE @low AS BIGINT = 1001, @high AS BIGINT = 1010;
WITH
L0 AS ( SELECT 1 AS c FROM (VALUES(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
L4 AS ( SELECT 1 AS c FROM L3 AS A CROSS JOIN L3 AS B ),
L5 AS ( SELECT 1 AS c FROM L4 AS A CROSS JOIN L4 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L5 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum;
There are many practical use cases for such a tool, including generating a series of date and time values, creating sample data, and more. Recognizing the common need, some platforms provide a built-in tool, such as PostgreSQL’s generate_series function. At the time of writing, T-SQL doesn’t provide such a built-in tool, but one can always hope and vote for such a tool to be added in the future.
In a comment to my article, Marcos Kirchner mentioned that he tested my solution with varying table value constructor cardinalities, and got different execution times for the different cardinalities.
I always used my solution with a base table value constructor cardinality of 2, but Marcos’ comment made me think. This tool is so useful that we as a community should join forces to try and create the fastest version that we possibly can. Testing different base table cardinalities is just one dimension to try. There could be many others. I’ll present the performance tests that I’ve done with my solution. I mainly experimented with different table value constructor cardinalities, with serial versus parallel processing, and with row mode versus batch mode processing. However, it could be that an entirely different solution is even faster than my best version. So, the challenge is on! I’m calling all jedi, padawan, wizard and apprentice alike. What’s the best performing solution that you can conjure? Do you have it within you to beat the fastest solution posted thus far? If so, share yours as a comment to this article, and feel free to improve any solution posted by others.
Requirements:
- Implement your solution as an inline table-valued function (iTVF) named dbo.GetNumsYourName with parameters @low AS BIGINT and @high AS BIGINT. As an example, see the ones I submit at the end of this article.
- You can create supporting tables in the user database if needed.
- You can add hints as needed.
- As mentioned, the solution should support delimiters of the BIGINT type, but you can assume a maximum series cardinality of 4,294,967,296.
- To evaluate the performance of your solution and compare it with others, I’ll test it with the range 1 through 100,000,000, with Discard results after execution enabled in SSMS.
Good luck to all of us! May the best community win. ;)
Different cardinalities for base table value constructor
I experimented with varying cardinalities of the base CTE, starting with 2 and advancing in a logarithmic scale, squaring the previous cardinality in each step: 2, 4, 16 and 256.
Before you start experimenting with different base cardinalities it could be helpful to have a formula that given the base cardinality and maximum range cardinality would tell you how many levels of CTEs you need. As a preliminary step, it’s easier to first come up with a formula that given the base cardinality and number of levels of CTEs, computes what’s the maximum resultant range cardinality. Here’s such a formula expressed in T-SQL:
DECLARE @basecardinality AS INT = 2, @levels AS INT = 5;
SELECT POWER(1.*@basecardinality, POWER(2., @levels));
With the above sample input values this expression yields a maximum range cardinality of 4,294,967,296.
Then, the inverse formula for computing the number of CTE levels needed involves nesting two log functions, like so:
DECLARE @basecardinality AS INT = 2, @seriescardinality AS BIGINT = 4294967296;
SELECT CEILING(LOG(LOG(@seriescardinality, @basecardinality), 2));
With the above sample input values this expression yields 5. Note that this number is in addition to the base CTE that has the table value constructor, which I named L0 (for level 0) in my solution.
Don’t ask me how I got to these formulas. The story I’m sticking to is that Gandalf uttered them to me in Elvish in my dreams.
Let’s proceed to performance testing. Make sure that you enable Discard results after execution in your SSMS Query Options dialog under Grid, Results. Use the following code to run a test with base CTE cardinality of 2 (requires 5 additional levels of CTEs):
DECLARE @low AS BIGINT = 1, @high AS BIGINT = 100000000;
WITH
L0 AS ( SELECT 1 AS c FROM (VALUES(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
L4 AS ( SELECT 1 AS c FROM L3 AS A CROSS JOIN L3 AS B ),
L5 AS ( SELECT 1 AS c FROM L4 AS A CROSS JOIN L4 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L5 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum;
I got the plan shown in Figure 1 for this execution.
Figure 1: Plan for base CTE cardinality of 2
The plan is serial, and all operators in the plan use row mode processing by default. If you’re getting a parallel plan by default, e.g., when encapsulating the solution in an iTVF and using a large range, for now force a serial plan with a MAXDOP 1 hint.
Observe how the unpacking of the CTEs resulted in 32 instances of the Constant Scan operator, each representing a table with two rows.
I got the following performance statistics for this execution:
CPU time = 30188 ms, elapsed time = 32844 ms.
Use the following code to test the solution with a base CTE cardinality of 4, which per our formula requires four levels of CTEs:
DECLARE @low AS BIGINT = 1, @high AS BIGINT = 100000000;
WITH
L0 AS ( SELECT 1 AS c FROM (VALUES(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
L4 AS ( SELECT 1 AS c FROM L3 AS A CROSS JOIN L3 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L4 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum;
I got the plan shown in Figure 2 for this execution.
Figure 2: Plan for base CTE cardinality of 4
The unpacking of the CTEs resulted in 16 Constant Scan operators, each representing a table of 4 rows.
I got the following performance statistics for this execution:
CPU time = 23781 ms, elapsed time = 25435 ms.
This is a decent improvement of 22.5 percent over the previous solution.
Examining wait stats reported for the query, the dominant wait type is SOS_SCHEDULER_YIELD. Indeed, the wait count curiously dropped by 22.8 percent compared to the first solution (wait count 15,280 versus 19,800).
Use the following code to test the solution with a base CTE cardinality of 16, which per our formula requires three levels of CTEs:
DECLARE @low AS BIGINT = 1, @high AS BIGINT = 100000000;
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum;
I got the plan shown in Figure 3 for this execution.
Figure 3: Plan for base CTE cardinality of 16
This time the unpacking of the CTEs resulted in 8 Constant Scan operators, each representing a table with 16 rows.
I got the following performance statistics for this execution:
CPU time = 22968 ms, elapsed time = 24409 ms.
This solution further reduces the elapsed time, albeit by just a few additional percent, amounting to a reduction of 25.7 percent compared to the first solution. Again, the wait count of the SOS_SCHEDULER_YIELD wait type keeps dropping (12,938).
Advancing in our logarithmic scale, the next test involves a base CTE cardinality of 256. It’s long and ugly, but give it a try:
DECLARE @low AS BIGINT = 1, @high AS BIGINT = 100000000;
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L2 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum;
I got the plan shown in Figure 4 for this execution.
Figure 4: Plan for base CTE cardinality of 256
This time the unpacking of the CTEs resulted in only four Constant Scan operators, each with 256 rows.
I got the following performance numbers for this execution:
CPU time = 23516 ms, elapsed time = 25529 ms.
This time it seems like the performance degraded a bit compared to the previous solution with a base CTE cardinality of 16. Indeed, the wait count of the SOS_SCHEDULER_YIELD wait type increased a bit to 13,176. So, it would seem that we found our golden number—16!
Parallel versus serial plans
I experimented with forcing a parallel plan using the hint ENABLE_PARALLEL_PLAN_PREFERENCE, but it ended up hurting performance. In fact, when implementing the solution as an iTVF, I got a parallel plan on my machine by default for large ranges, and had to force a serial plan with a MAXDOP 1 hint to get optimal performance.
Batch processing
The main resource used in the plans for my solutions is CPU. Given that batch processing is all about improving CPU efficiency, especially when dealing with large numbers of rows, it’s worthwhile to try this option. The main activity here that can benefit from batch processing is the row number computation. I tested my solutions in SQL Server 2019 Enterprise edition. SQL Server chose row mode processing for all previously shown solutions by default. Apparently, this solution didn’t pass the heuristics required to enable batch mode on rowstore. There are a couple of ways to get SQL Server to use batch processing here.
Option 1 is to involve a table with a columnstore index in the solution. You can achieve this by creating a dummy table with a columnstore index and introduce a dummy left join in the outermost query between our Nums CTE and that table. Here’s the dummy table definition:
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
Then revise the outer query against Nums to use FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0. Here’s an example with a base CTE cardinality of 16:
DECLARE @low AS BIGINT = 1, @high AS BIGINT = 100000000;
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum;
I got the plan shown in Figure 5 for this execution.
Figure 5: Plan with batch processing
Observe the use of the batch mode Window Aggregate operator to compute the row numbers. Also observe that the plan doesn’t involve the dummy table. The optimizer optimized it out.
The upside of option 1 is that it works in all SQL Server editions and is relevant in SQL Server 2016 or later, since the batch mode Window Aggregate operator was introduced in SQL Server 2016. The downside is the need to create the dummy table and include it in the solution.
Option 2 to get batch processing for our solution, provided that you’re using SQL Server 2019 Enterprise edition, is to use the undocumented self-explanatory hint OVERRIDE_BATCH_MODE_HEURISTICS (details in Dmitry Pilugin’s article), like so:
DECLARE @low AS BIGINT = 1, @high AS BIGINT = 100000000;
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum
OPTION(USE HINT('OVERRIDE_BATCH_MODE_HEURISTICS'));
The upside of option 2 is that you don’t need to create a dummy table and involve it in your solution. The downsides are that you need to use Enterprise edition, use at minimum SQL Server 2019 where batch mode on rowstore was introduced, and the solution involves using an undocumented hint. For these reasons, I prefer option 1.
Here are the performance numbers that I got for the various base CTE cardinalities:
Cardinality 2: CPU time = 21594 ms, elapsed time = 22743 ms (down from 32844). Cardinality 4: CPU time = 18375 ms, elapsed time = 19394 ms (down from 25435). Cardinality 16: CPU time = 17640 ms, elapsed time = 18568 ms (down from 24409). Cardinality 256: CPU time = 17109 ms, elapsed time = 18507 ms (down from 25529).
Figure 6 has a performance comparison between the different solutions:
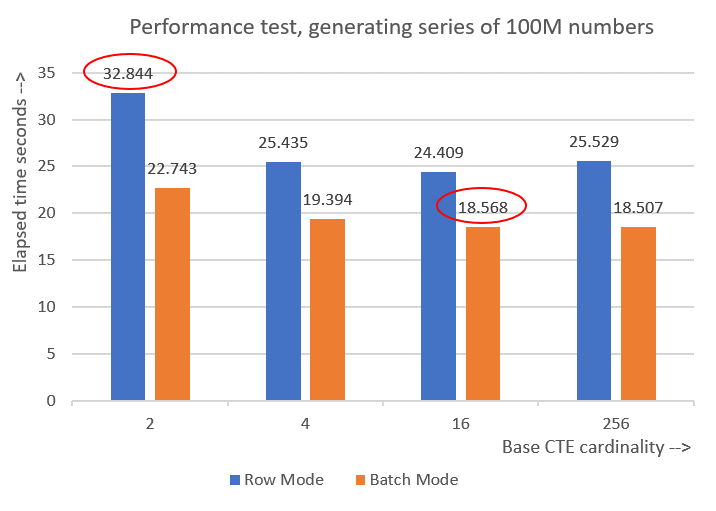Figure 6: Performance comparison
You can observe a decent performance improvement of 20-30 percent over the row mode counterparts.
Curiously, with batch mode processing the solution with base CTE cardinality of 256 did best. However, it’s just a tiny bit faster than the solution with base CTE cardinality of 16. The difference is so minor, and the latter has a clear advantage in terms of code brevity, that I’d stick to 16.
So, my tuning efforts ended up yielding an improvement of 43.5 percent from the original solution with the base cardinality of 2 using row mode processing.
The challenge is on!
I submit two solutions as my community contribution to this challenge. If you’re running on SQL Server 2016 or later, and are able to create a table in the user database, create the following dummy table:
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
And use the following iTVF definition:
CREATE OR ALTER FUNCTION dbo.GetNumsItzikBatch(@low AS BIGINT, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum;
GO
Use the following code to test it (make sure to have Discard results after execution checked):
SELECT n FROM dbo.GetNumsItzikBatch(1, 100000000) OPTION(MAXDOP 1);
This code finishes in 18 seconds on my machine.
If for whatever reason you cannot meet the batch processing solution’s requirements, I submit the following function definition as my second solution:
CREATE OR ALTER FUNCTION dbo.GetNumsItzik(@low AS BIGINT, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum;
GO
Use the following code to test it:
SELECT n FROM dbo.GetNumsItzik(1, 100000000) OPTION(MAXDOP 1);
This code finishes in 24 seconds on my machine.
Your turn!
This subject is right up my ally as I have been writing about it a lot. For fun, I made a couple changes to dbo.getnums (named getnums2 below) which will speed things up and give it some cool new functionality.
CREATE FUNCTION dbo.GetNums2(@low AS BIGINT, @high AS BIGINT)
RETURNS TABLE WITH SCHEMABINDING AS RETURN
WITH
L0 AS (SELECT c FROM (SELECT 1 UNION ALL SELECT 1) AS D(c)), — 2
L1 AS (SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B), — 4
L2 AS (SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B), — 16
L3 AS (SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B), — 256
L4 AS (SELECT 1 AS c FROM L3 AS A CROSS JOIN L3 AS B), — 65,536
L5 AS (SELECT 1 AS c FROM L4 AS A CROSS JOIN L4 AS B), — 4,294,967,296
Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L5)
SELECT TOP(@high – @low + 1)
RN = rownum,
OP = @high + @low – (@low + rownum – 1),
N = @low + rownum – 1
FROM Nums
ORDER BY rownum;
Usage Example:
DECLARE @low BIGINT = -2,
@high BIGINT = 3
SELECT f.*
FROM dbo.GetNums2(@low,@high) AS f
ORDER BY f.RN;
RETURNS:
RN N OP
——————– ——————– ——————–
1 -2 3
2 -1 2
3 0 1
4 1 0
5 2 -1
6 3 -2
If you need the numbers 1 to ? You can use the "Row Number" col which does not require any additional computation; @low+@High-rownum-1 does add a bit of overhead.
Below is a test I put together quickly to compare:
1. The varchar(max) version of my Ngrams function as a numbers table
(https://www.sqlservercentral.com/articles/nasty-fast-n-grams-part-1-character-level-unigrams)
2. getnums
3. getnums2
4. fnTally by Jeff Moden (https://www.sqlservercentral.com/scripts/create-a-tally-function-fntally)
THE TEST:
SET STATISTICS TIME ON;
DECLARE @low BIGINT = 1,
@high BIGINT = 100000000;
DECLARE @N BIGINT;
–==== 1. My N-Grams Function
PRINT CHAR(13)+'dbo.NGams – VARCHAR(MAX) version'+CHAR(13)+REPLICATE('-',90);
SELECT @N = ng.Position
FROM samd.ngrams(REPLICATE(CAST('0' AS VARCHAR(MAX)),@high),1) AS ng;
–==== 2. GetNums using N
PRINT CHAR(13)+'GetNums using N; N as a derived value'+CHAR(13)+REPLICATE('-',90);
SELECT @N = f.N
FROM dbo.GetNums(@low,@high) AS f;
–==== 3. GetNums using N With Order BY
PRINT CHAR(13)+'GetNums using N With Order BY – gets a sort'+CHAR(13)+REPLICATE('-',90);
SELECT @N = f.N
FROM dbo.GetNums(@low,@high) AS f
ORDER BY f.N
–==== 4. GetNums2 using RN With Order BY
PRINT CHAR(13)+'GetNums using RN With Order BY – No Sort'+CHAR(13)+REPLICATE('-',90);
SELECT @N = f.RN
FROM dbo.GetNums2(@low,@high) AS f
ORDER BY f.RN;
–==== 5. GetNums2 return the numbers in DESC order – Still No sort
PRINT CHAR(13)+'GetNums with "N" in DESC order – Still No sort'+CHAR(13)+REPLICATE('-',90);
SELECT @N = f.RN
FROM dbo.GetNums2(@low,@high) AS f
ORDER BY f.RN;
–==== 6. Jeff Moden – FnTally
PRINT CHAR(13)+'Jeff Moden – FnTally'+CHAR(13)+REPLICATE('-',90);
SELECT @N = f.N
FROM dbo.fnTally(@low,@high) AS f
ORDER BY f.N;
SET STATISTICS TIME OFF;
RESULTS:
dbo.NGams – VARCHAR(MAX) version
——————————————————————————————
SQL Server Execution Times: CPU time = 11485 ms, elapsed time = 11614 ms.
GetNums using N; N as a derived value
——————————————————————————————
SQL Server Execution Times: CPU time = 18953 ms, elapsed time = 19016 ms.
GetNums using N With Order BY – gets a sort
——————————————————————————————
SQL Server Execution Times: CPU time = 80656 ms, elapsed time = 89678 ms.
GetNums2 using RN With Order BY – No Sort
——————————————————————————————
SQL Server Execution Times: CPU time = 15141 ms, elapsed time = 15132 ms.
GetNums2 with "N" in DESC order – Still No sort
——————————————————————————————
SQL Server Execution Times: CPU time = 15359 ms, elapsed time = 15489 ms.
Jeff Moden – FnTally
——————————————————————————————
SQL Server Execution Times: CPU time = 12235 ms, elapsed time = 12239 ms.
Lastly – have a look at rangeAB and rangeAB2. RangeAB sits a top fnTally, rangeAB2 uses a physical numbers table. Here's the functions:
https://codingblackarts.com/recommended-reading/using-rangeab-and-rangeab2/
Here's an interesting use of both for an interesting Prime Numbers problem I came up with:
https://codingblackarts.com/2020/12/08/virtual-indexing-part-3-the-indexed-function/
Does the function need to return ordered results?
Hi Joe,
No it doesn't.
Cheers,
Itzik
I opted for creating a CCI with 134217728 rows of sequential integers. The function reference the table up to 32 times to get all of the rows needed for the result set. I chose a CCI because the data will compress well (less than 3 bytes per row), you get batch mode "for free", and previous experience suggests that reading sequential numbers from a CCI will be faster than generating them through some other method. Full code is here: https://gist.github.com/jobbish-sql/3792fe243240a4d760348e75ebddf4c2 , although there may be some off-by-one errors.
On my machine, here's what I get with my solution using the required testing methodology:
CPU time = 6656 ms, elapsed time = 9510 ms.
Here's what I get for the same test using the function supplied in the article:
CPU time = 9750 ms, elapsed time = 10126 ms.
With all of that said, I wonder what it really means for a solution to be the "fastest" for this type of function. As far as I can tell, nearly all of the query's time is spent sending the rows to SSMS. I can't optimize away the nearly 3 seconds of ASYNC_NETWORK_IO wait. It's true that those waits can change by switching from batch mode to row mode or by adding parallelism to the query but neither one of those accomplishes anything meaningful here. Beyond that wait, I suspect that I can only optimize about ten percent of the query's runtime. For example, taking a brief look at callstacks shows that about half of them are included under sqllang!CTds74::SendRowImpl. There's nothing I can do as a query tuner about that CPU work.
If you're looking for a gold standard solution for a generate_series function then I believe you'll have to consider other factors such as the cardinality estimate of the function itself and how well the function performs when plugged into more realistic queries. I acknowledge that you may have been planning to do that at a future date. There's certainly value in collecting solutions from the community even if the test case isn't all-encompassing.
Joe – changing SSMS query results options to discard the results does optimize away the 3 seconds that it takes to send to SSMS as it won’t spend the time to display the results once it gets them.
You can declare a bigint then use it to capture the value. E.g Replace "SELECT N…" with "SELECT @N = N…"
I frequently teach about the cCTE (cascading CTE) method that Itzik came up with long ago (and some of the various permutations others have come up with) and demonstrate both its usage and its speed.
I also tell folks that Front End Developers laugh at us because compiled code will make us look like we're running backwards.
With that last statement, I strongly suspect that a CLR will smoke any of our attempts using pure T-SQL to solve the problem.
Now, shifting gears a bit, while it's a bit of fun competing in such T-SQL races, there's a much better place for us to expend our energy and that place can be found at the following link.
https://feedback.azure.com/forums/908035-sql-server/suggestions/32890519-add-a-built-in-table-of-numbers
The link was started by Erland Sommarskog way back in February of 2007. It had gained 278 votes as a "CONNECT" item and then they switched to Azure "FEEDBACK" and all votes were lost. It has accumulated 190 votes since then.
As Adam Machanic, Itzik Ben-Gan, and others have proven, it's not difficult to create an incredibly fast function through CLR but that's not the point either.
What is the point is that Microsoft has kept the item open with no action since 2007 and, apparently they can't see the grand utility in having such a thing.
Instead of us wasting time in a fun but useless manner, we should be canvasing the world to finally get Microsoft to move off top-dead-center and include such a thing as a native part of T-SQL. If you haven't voted at the link I provided above, please do so today. Then, spread the word. It's just stupid that Microsoft has delayed now for almost 14 years.
While you're there, vote on them also fixing the String_Split function so the it returns the ordinal position of each returned element. Here's the link.
https://feedback.azure.com/forums/908035-sql-server/suggestions/32902852-add-row-position-column-to-string-split?tracking_code=448131ee0df3b7ecd79493c0c5068495
I don't think anyone has taken compile times into account.
Bear in mind most people use these functions for much smaller numbers of rows than 2^32
I'm getting much longer compile times for the 256 option, this is independent of batch mode.
2: 22ms
4: 9ms
16: 7ms
256: 35ms
I tried removing the CTEs and doing just L0 as a CTE cross joined 8 times, it knocked off 1ms compile time, to 6ms.
I got a perf advantage on execution, by flipping round the final result to "@low – 1 + rownum AS n", the theory is the compiler will recognize @low -1 as a constant and pre-calculate it.
Another optimization is to remove @low completely, because most people want to start from 1, if you need something else you can always adjust the final value in your own query
Charlie…
Ordinarily, I'd say that paying attention to compile times is important but compiles times don't actually matter on such a repetitive use piece of code where re-compiles are not going to be a factor.
They'd really not matter if MS would move off top-dead-center after almost 14 years and integrate a CLR function into T-SQL.
@Jeff Moden:
Compile times will matter in an inline TVF, as it will be inlined into whichever query you are writing and compiled together with it. There is no query plan cache for an iTVF separate from the query that uses it.
Agreed that this is beyond stupid from MS.
My top list of things for MS to get on with, in order of precedence:
Fix all known MERGE bugs
Fix all known filtered index limitations
IS (DISTINCT FROM) syntax, to compare nullables
Index skip-scanning
MEDIAN aggregate function
Tally/numbers table
Trigram indexing, for efficient LIKE
STRING_SPLIT rownumber and accept varbinary, STRING_AGG accept varbinary
Allowing grouped subquery (left join with group by) in indexed view, this allows denormalized SUM/COUNT without triggers
This list is absolute PRIORITY, far above any other new features. I think most well-versed DBAs and developers would agree.
Hi Itzik,
I defently sure that it is the best code and best solution.
But I realize that many commercial company are avoid and reluctant to use. because only few programmers, in all over the world, can hold and customize such code.
@Charile,
The compile times won't matter unless you have a poor query that recompiles every time that it's executed.
The bottom line is the same as with all else in SQL Server… "It Depends".
"I got a perf advantage on execution, by flipping round the final result to '@low – 1 + rownum AS n',"
The problem is that you are performing a calculation for each for row. Note the performance test I posted above. Returning rownum (ROW_NUMBER), as-is, will perform the better. For this exercise an expression-free ordered set is not required but is my preference because:
1. It is faster
2. The numbers as an ordered set can be grouped, aggregated, enjoy window functions or TOP(N)… all without a sort.
3. It's far more performant to join rownum to another number than it using "@low – 1 + rownum AS n"
With that in mind – the proof is in the pudding so I put together an example of how powerful a correctly assembled numbers table function can be by building a faster alternative to NTILE which reduces reads by 99%+
https://codingblackarts.com/2020/12/10/virtual-indexing-part-4-the-ntally-table/
I think we've only begun to scratch the surface of what we can do with a numbers table.
Hello Itzik,
I hope you are doing well.
I've tried with the CLR function. It runs in around 27secs on my system (100 mil rows), so decent performance, but doesn't beat the best ones out there.
Example usage select * from dbo.GetNums_KamilKosno(1,100000000);
And of course needs to be deployed with custom assembly.
using System;
using System.Data.SqlTypes;
using System.Collections;
public partial class UserDefinedFunctions
{
[Microsoft.SqlServer.Server.SqlFunction (FillRowMethodName= "GetNums_Fill", TableDefinition ="n BIGINT")]
public static IEnumerator GetNums_KamilKosno(SqlInt32 low, SqlInt32 high)
{
return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0) : new GetNumsCS(low.Value, high.Value);
}
public static void GetNums_Fill(Object o, out SqlInt64 n)
{
n = (long)o;
}
private class GetNumsCS : IEnumerator
{
public GetNumsCS(long from, long to)
{
_lowrange = from;
_current = _lowrange -1;
_highrange = to;
}
public bool MoveNext()
{
_current += 1;
if (_current > _highrange) return false;
else return true;
}
public object Current
{
get
{
return _current;
}
}
public void Reset()
{
_current = _lowrange – 1;
}
long _lowrange;
long _current;
long _highrange;
}
}
My approach was similar to Joe Obbish's: https://gist.github.com/BeginTry/66e20be7001683b67bf98054a0359b86
I created a clustered columnstore index on a table with a single BIT column. It was populated with the full 4294967296 rows. (With COLUMNSTORE_ARCHIVE compression, the table only required 3.44 MB on disk). My TVF selects ROW_NUMBER() from the table.
With SET STATISTICS IO, TIME ON, I get CPU time and Elapsed times ~1000ms quicker than what I got when testing Itzik's solution.
My approach was a bit slower than Joe Obbish's: his CPU time was 1000-2000ms faster, although Elapsed times were nearly the same. I had the edge in lob logical reads with just 384 vs 32928 for Joe.
Other attempts:
I tried a .NET CLR TVF, which yielded CPU time and Elapsed time both consistently about 30,000ms. This was slower than I expected. I hadn't written CLR code for SQL in years, and this was the first TVF I had written. The "FillRow" method required for a TVF and the .NET gymnastics of creating a Classs object for every row returned seemed like a lot of overhead for something that's really simple in concept.
I also tried sp_execute_external_script with R. This was really fast, but still a few hundred milliseconds slower than Itzik's solution. Plus, you can't execute a stored proc from within a TSQL Table Valued Function, which was a requirement for the challenge. (I could "cheat" and use OPENQUERY from within a TSQL TVF, but performance was terrible.)
Additionally, I tried STRING_SPLIT( ). I had guessed that the function was running C or C++ code under the covers and might be faster than run-time TSQL. Generating the first 100K numbers only too ~140ms. But as I continued higher to 1 million and beyond, performance grew progressively worse.
I had also considered an old-school extended stored proc (written in C?… C++?). But I've never written one of those before, and I'm not even sure it's still supported. I'm thinking they're deprecated at the least.
Did anyone look at what Alan B. Has written? Nobody has made comment, so I'm wondering if everyone skimmed over it. Took me a few to grasp what he's done but that stuff is next level. There are some principles in there im definitely poaching
Hi John,
I’m going to write a follow up article next month covering the different solutions that people posted. Lots of great ideas here! Keep 'em coming!
Itzik
@John thank you sooooo much. Self esteem = 50,000
Hello (Happy New Year!)
I have experimented a bit more with the CLR, and one of the things I came up with is a hybrid function T-SQL + CLR. It's probably not something you would like to create, but it did give me interesting results of being much quicker than the original. I had to add a new step functionality to the original CLR routine. This step results in only every n-th number being returned, while we fill in the gaps with a t-sql subquery. This solution ran in about 11 seconds on my system (original around 27secs).
Use example:
select n from dbo.GetNums_Hybrid_Kamil(1, 100000000)
CLR part:
using System;
using System.Data.SqlTypes;
using System.Collections;
public partial class UserDefinedFunctions
{
[Microsoft.SqlServer.Server.SqlFunction (DataAccess = Microsoft.SqlServer.Server.DataAccessKind.None, IsDeterministic = true, IsPrecise = true, FillRowMethodName= "GetNums_Fill", TableDefinition ="n BIGINT")]
public static IEnumerator GetNums_KamilKosno(SqlInt64 low, SqlInt64 high, SqlInt64 step)
{
return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0, step.Value) : new GetNumsCS(low.Value, high.Value, step.Value);
}
public static void GetNums_Fill(Object o, out SqlInt64 n)
{
n = (long)o;
}
private class GetNumsCS : IEnumerator
{
public GetNumsCS(long from, long to, long step)
{
_lowrange = from;
_step = step;
_current = _lowrange – _step;
_highrange = to;
}
public bool MoveNext()
{
_current = _current + _step;
if (_current > _highrange) return false;
else return true;
}
public object Current
{
get
{
return _current;
}
}
public void Reset()
{
_current = _lowrange – _step;
}
long _lowrange;
long _current;
long _highrange;
long _step;
}
}
T-SQL function:
CREATE OR ALTER FUNCTION dbo.GetNums_Hybrid_Kamil(@low AS BIGINT, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
select top(@high – @low + 1)v.n
from
dbo.GetNums_KamilKosno(@low,@high,10) as gn
cross apply
(values(0 + gn.n),(1 + gn.n),(2 + gn.n),(3 + gn.n),(4 + gn.n),(5 + gn.n),(6 + gn.n),(7 + gn.n),(8 + gn.n),(9 + gn.n)) as v(n);
GO
Just for pure performance sake, I have now tried to find a limit for the same solution, which appears to be around step 20. It allows to consistently get times below 10 seconds. CLR solution which is part of it, is quite efficient as it doesn't actually build the table in memory before sending the rows, and perhaps the step functionality could also be useful, so maybe there are use cases after all..
I am not repeating the CLR part as it has not changed. Here is the changed T-SQL part.
CREATE or alter FUNCTION [dbo].[GetNums_Hybrid_Kamil](@low AS BIGINT, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
select top(@high – @low + 1)v.n
from
dbo.GetNums_KamilKosno(@low,@high,20) as gn
cross apply
(values(0 + gn.n),(1 + gn.n),(2 + gn.n),(3 + gn.n),(4 + gn.n),(5 + gn.n),(6 + gn.n),(7 + gn.n),(8 + gn.n),(9 + gn.n),
(10 + gn.n),(11 + gn.n), (12 + gn.n), (13 + gn.n), (14 + gn.n), (15 + gn.n), (16 + gn.n), (17 + gn.n), (18 + gn.n), (19 + gn.n)
) as v(n)
GO
As a bit of a sidebar…
The "rules" for this function are to allow the selection of a low value and a high value and that prompts a question in my mind. As a preamble to my question, I need a sequence that starts at "1" about 95% of the time and a sequence that starts at 0 about 4.9% of the time. It's a very rare thing (about 0.1%) of the time where I need a sequence that starts at something other than "0" or "1".
With that, I'll ask the question of all of you (including you, please, Itzik)…
As a percentage of your total usage of any sequence generator, how often have you actually needed a sequence that starts at something other than "0" or "1"?
Thanks for any answers, folks.
Hello Jeff, In my case I don't recall a time when I used something other than 0 or 1
Hi Jeff,
Indeed most of the times I use 1 or 0, but occasionally I do get to use other low/high bounds. Examples include generating sample data where I use the number series generator to generate a range of keys, such as order IDs, e.g., in the range 1000001 through 2000000.
Another example would be generating an uninterrupted sequence of keys between the min/max keys that exist in a table, perhaps to identify the individual missing keys:
select n
from dbo.getnums((select min(orderid) from sales.orders),
(select max(orderid) from sales.orders)) as nums
except
select orderid from sales.orders;
But again, in most cases I use it with 1 or 0.
Thanks for your feedback, Kamil and Itzik. Much appreciated.
With that (and I believe most people will say the same as the two of you have stated about the need for other than a "0" or "1" starting value being a bit rare), any of the extra math (no matter how trivial) to support otherwise simply slows the function down.
And with that thought in mind and the fact that it's quite easy to do such math external to the function and only on the rare occasions when it's actually needed, why are we building that guaranteed slow-down into the function, which affects all of the usage even when we need to just start at "1" almost all of the time (for example)?
Jeff, sure, if that's what works for you. I can also see an option of maintaining two versions of the function–one that starts with 1 or 0 (for most cases and for the performance benefit), and another with the range, for convenience, for the cases where it's needed.
Thanks, Itzik. Considering that I've needed a starting value other than "0" or "1" maybe twice in 2 decades, I'll stick with the original rendition of your brilliant work from years ago.
I'm just really curious how many other people regularly need a starting value other than "0" or "1" and what the reason was.
BTW, Jeff, Alan's suggested revision (dbo.GetNums2), returning N (@low-based sequence), OP (opposite) and RN (1-based sequence), cleverly addresses the common/occasional use issue without the need to maintain multiple functions. Being an inline TVF, when you query only RN, you don't pay the extra overhead due to the computation involved with N. That's so simple and pretty neat at the same time!
Itzik, agreed, and the perf issue is what I said earlier.
Charlie, yes you did. BTW, your constant folding trick is brilliant. I love it! :) It knocked off about 5% from the execution time.
I also agree with you about compilation time improvements. Most tend to focus on just execution times, but as you say, the function is often used with small ranges, and compilation times can become a significant portion. Thanks for sharing your findings!
Itzik,
These "static" tests are a lot of fun, especially since it keeps the "rules" of a competition very straight forward and simple. Even having the output dump to variables to simulate "in memory" use is a great idea for some real world applications.
But… even the latter method doesn't cover "most" of the real world applications. For example, SET STATISTICS TIME ON or setup to capture stats using SQL Profiler or Extended Events and then modify the test code for GetNums, GetNums2, and fnTally to do a simple SELECT/INTO a Temp Table and see some differences that the other tests simply don't show. You'll be seriously surprised even with such things as a combine function with a supposed "optimization" for an RN that starts at 1.
If necessary, I can formalize the code I used for such a test and can publish it here but it's simple enough to do.
Seriously… try it and see.
Is there a pure SQL way to do a SHA1 hash? I don't mean hashbytes, I mean like a natively compiled function/proc which does the actual bitwise manipulation to generate the digest…I'm looking at the pseudo-code on the wikipedia article for SHA1 (https://en.wikipedia.org/wiki/SHA-1) and it certainly seems like it's straightforward. Is there anything there that wouldn't be doable from straight SQL? I'm interested in seeing if we could make something to compete with hashbytes. I've seen so many examples lately where doing the math yourself vs using built-in SQL commands is actually significantly faster. Wondering if that could apply to hashbytes VS doing the hash math ourselves?
@JohnNumber2
For that kind of function, either CLR or C++ is going to be the fastest by far, because you are doing a huge amount of processing on each single value. I believe it can be even faster than HASHBYTES.
Whereas in our case, we are not doing any calculation at all except for the counter, and most of the overhead is in generating empty rows as fast as possibe, for which CLR isn't great, as the overhead there is in passing data to/from the C++ execution engine.
I agree, Charlie. It's interesting how many people intuitively felt that a CLR-based solution for the number series generator would easily outperform set-based solutions. But for this type of task, where like you say the main part is generating a large set of rows, a good set-based solution has better potential.
Sorry, I didn't mean to imply CLR, I was thinking straight SQL math, not CLR. I realize after re-reading what I typed, that I said "natively compiled" but that's not what I meant. Too many in-memory projects lately :)
Thing is, this whole thread has me seeing little tricks like that constant-folding trick, Alan's NTILE replacement and other things all adding up to many percent increase in performance when added together. So I got to thinking that what if we can think about SHA1 in a set-based way. Like instead of an iteration through a loop 80 times, we think about it in terms of set-based… an 80-row tally, some bitwise operations on the current chunk, maybe a LAG() in there to work with the results from the last iteration, etc. Is there any chance that competes with HASHBYTES?
Hi John,
I think that both Charlie and I understood your original intent in that you are evaluating the potential for a pure SQL/T-SQL set-based solution for SHA1.
I have to say that I haven't given it very careful consideration yet; it's just that generally such tasks are the type that tend to perform better with a language that is optimal with iterative/procedural logic, hence the thinking about CLR or C++. But I could be wrong. It could be worthwhile to give it a try. :)
Hi Jeff,
Most tests indeed show that a 1-based sequence (I'll call it rn) performs a bit better than a @low-based sequence (I'll call it n). I get about 5% improvement in most tests. That's the case with discard results after execution, as well as with the SELECT INTO #TempTable option.
I think that we're all in agreement.
What's nice about the improvements by Alan and Charlie is that you can have your cake and eat it too. ;)
Have both rn and n (and op) returned.
With the constant folding trick, you can ORDER BY rn or n and not pay a sort penalty either way.
Return rn when you need a 1-based sequence, n when you need a @low-based sequence, and op when you need reverse order.
I summarize all this in an article that will be published next Wednesday.
In the meanwhile, I followed your suggestion to test a SELECT INTO version.
Here's the batch-mode version of my function with Alan's and Charlie's improvements:
— dbo.GetNumsAlanCharlieItzikBatch
— Dummy table
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
GO
— Function definition
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high – @low + 1)
rownum AS rn,
@high + 1 – rownum AS op,
@low – 1 + rownum AS n
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum;
GO
Here's the row-mode version of my function with Alan's and Charlie's improvements:
— dbo.GetNumsAlanCharlieItzik
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzik(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high – @low + 1)
rownum AS rn,
@high + 1 – rownum AS op,
@low – 1 + rownum AS n
FROM Nums
ORDER BY rownum;
GO
And here's the performance test:
— CPU time = 17031 ms, elapsed time = 18279 ms.
— 1-based sequence, row mode, base CTE cardinality 256, results discarded
SELECT N FROM dbo.fnTally(1, 100000000) OPTION(MAXDOP 1);
— CPU time = 20766 ms, elapsed time = 20772 ms.
— 1-based sequence, row mode, base CTE cardinality 256, into #TempTable
DROP TABLE IF EXISTS #T;
SELECT N INTO #T FROM dbo.fnTally(1, 100000000) OPTION(MAXDOP 1);
DROP TABLE IF EXISTS #T;
— CPU time = 15937 ms, elapsed time = 17217 ms.
— @low-based sequence, batch mode, base CTE cardinality 16, results discarded
SELECT n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
— CPU time = 19281 ms, elapsed time = 19350 ms.
— @low-based sequence, batch mode, base CTE cardinality 16, into #TempTable
DROP TABLE IF EXISTS #T;
SELECT n INTO #T FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
DROP TABLE IF EXISTS #T;
— CPU time = 15282 ms, elapsed time = 18704 ms.
— 1-based sequence, batch mode, base CTE cardinality 16, results discarded
SELECT rn FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
— CPU time = 17531 ms, elapsed time = 17590 ms.
— 1-based sequence, batch mode, base CTE cardinality 16, into #TempTable
DROP TABLE IF EXISTS #T;
SELECT rn INTO #T FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
DROP TABLE IF EXISTS #T;
— CPU time = 18906 ms, elapsed time = 20238 ms.
— @low-based sequence, row mode, base CTE cardinality 16, results discarded
SELECT n FROM dbo.GetNumsAlanCharlieItzik(1, 100000000) OPTION(MAXDOP 1);
— CPU time = 22406 ms, elapsed time = 22473 ms.
— @low-based sequence, row mode, base CTE cardinality 16, into #TempTable
DROP TABLE IF EXISTS #T;
SELECT n INTO #T FROM dbo.GetNumsAlanCharlieItzik(1, 100000000) OPTION(MAXDOP 1);
DROP TABLE IF EXISTS #T;
— CPU time = 17657 ms, elapsed time = 18972 ms.
— 1-based sequence, row mode, base CTE cardinality 16, results discarded
SELECT rn FROM dbo.GetNumsAlanCharlieItzik(1, 100000000) OPTION(MAXDOP 1);
— CPU time = 21797 ms, elapsed time = 21851 ms.
— 1-based sequence, row mode, base CTE cardinality 16, into #TempTable
DROP TABLE IF EXISTS #T;
SELECT rn INTO #T FROM dbo.GetNumsAlanCharlieItzik(1, 100000000) OPTION(MAXDOP 1);
DROP TABLE IF EXISTS #T;
I really like where it's going, since the improvements are really meaningful. :)
Cheers,
Itzik
Sure… now turn on Statistics I/O and see "the rest of the story". :D
"…I could be wrong. It could be worthwhile to give it a try. :)"
Itzik, I'd be willing to give it a first pass which then we can optimize…I'm just not sure I understand what some of the things mean, or how to do them with SQL…
"append 0 ≤ k < 512 bits '0', such that the resulting message length in bits is congruent to −64 ≡ 448 (mod 512)"
umm…..
that is, I took computer logic and math courses in college, so I get MOD, XOR, AND, etc. and I understand doing bitwise vs regular operations…but knowing exactly what is meant by some of the pseudocode (or the actual text of the standards PDF) and how to do exactly in SQL so we get the same result, that gives me pause
Also, where should I take this discussion so I don't pollute the topic of THIS particular challenge?
#2
Hi Jeff,
Not sure what the rest of the story is supposed to be? STATISTICS IO has nothing to report when there's no physical source table to query, so turning it ON produces no output in all SELECT INTO tests that I posted. I did run an extended events session to measure I/O costs, and got an identical number in all tests. See below:
— CPU time = 20766 ms, elapsed time = 20772 ms.
— logical reads: 145425, writes: 0
— 1-based sequence, row mode, base CTE cardinality 256, into #TempTable
SELECT N INTO #T FROM dbo.fnTally(1, 100000000) OPTION(MAXDOP 1);
DROP TABLE IF EXISTS #T;
— CPU time = 19281 ms, elapsed time = 19350 ms.
— logical reads: 145425, writes: 0
— @low-based sequence, batch mode, base CTE cardinality 16, into #TempTable
SELECT n INTO #T FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
DROP TABLE IF EXISTS #T;
— CPU time = 17531 ms, elapsed time = 17590 ms.
— logical reads: 145425, writes: 0
— 1-based sequence, batch mode, base CTE cardinality 16, into #TempTable
SELECT rn INTO #T FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
DROP TABLE IF EXISTS #T;
— CPU time = 22406 ms, elapsed time = 22473 ms.
— logical reads: 145425, writes: 0
— @low-based sequence, row mode, base CTE cardinality 16, into #TempTable
SELECT n INTO #T FROM dbo.GetNumsAlanCharlieItzik(1, 100000000) OPTION(MAXDOP 1);
DROP TABLE IF EXISTS #T;
— CPU time = 21797 ms, elapsed time = 21851 ms.
— logical reads: 145425, writes: 0
— 1-based sequence, row mode, base CTE cardinality 16, into #TempTable
SELECT rn INTO #T FROM dbo.GetNumsAlanCharlieItzik(1, 100000000) OPTION(MAXDOP 1);
DROP TABLE IF EXISTS #T;
Am I missing something?
OMG, thank you, I noticed that exact thing this morning. Thought I was doing something wrong because I was getting no output after turning STATISTICS IO on…but in another database on the same server it was working just fine.
(meaning, that other queries which touch actual tables were returning IO information)
Sure thing, John. :)
Just to codify a version I had which performs better than the others (at least on my laptop it does) which I think was similar to something Dave Mason was doing…a super tiny dummy table (1.6MB) with no data. These are the rows upon which ROW_NUMBER() will do its work
/* Dummy table to hold 4294967296 empty rows */
CREATE TABLE dbo.NullBits(b BIT NULL);
GO
/* Clustered columnstore index with COLUMNSTORE_ARCHIVAL compression for smallest footprint */
CREATE CLUSTERED COLUMNSTORE INDEX cc_NullBits ON dbo.NullBits WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE);
GO
/*
Fill the NullBits table with 4294967296 NULL bits
NOTE: This takes 20 minutes on my laptop, but only requires 1.6 MB of disk space when it's done!
*/
WITH
L0 AS (SELECT CONVERT(BIT,NULL) b FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
L1 AS (SELECT A.b FROM L0 A CROSS JOIN L0 B),
L2 AS (SELECT A.b FROM L1 A CROSS JOIN L1 B),
nulls(b) AS (SELECT A.b FROM L2 A CROSS JOIN L2 B)
INSERT INTO dbo.NullBits(b)
SELECT b FROM nulls OPTION(MAXDOP 1);
/*
John Number2 version of the function using the 1.6MB NullBits table and Alan's TOP optimization
*/
CREATE FUNCTION dbo.GetNumsJohn2 (
@low AS BIGINT,
@high AS BIGINT
)
RETURNS TABLE
AS
RETURN
WITH
Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum FROM dbo.NullBits)
SELECT TOP(@high – @low + 1)
rownum AS rn,
@high + 1 – rownum AS op,
@low – 1 + rownum AS n
FROM
Nums
ORDER BY
rownum;
/* John Number2 version test */
DROP TABLE IF EXISTS #T;
SELECT rn INTO #T FROM dbo.GetNumsJohn2(1, 100000000) OPTION(MAXDOP 1);
DROP TABLE IF EXISTS #T;
–GetNumsJohn2
–CPU time = 20563 ms, elapsed time = 20755 ms.
–GetNumsAlanCharlieItzikBatch
–CPU time = 25563 ms, elapsed time = 25932 ms.
My thoughts on what's going on is this is kind of a hybrid between a fully in-memory tally (Itzik) and a physical integers table.
In the case of an in-memory tally, it has no physical IO but the engine has to make all those rows and ROW_NUMBER() puts numbers in them which is quick, to be sure, but it still needs to do that work.
In the case of a physical integers table, the rows already exist and the integers are already generated so the engine doesn't need to create rows and ROW_NUMBER() doesn't have to generate the integers, but it still has to physically move bytes from pages.
In this version, we're kind of between those two paradigms. The rows don't need to be generated because we've already got a recordset with 4294967296 rows ready to be overlaid with integers by ROW_NUMBER(), so less row-making work compared to in-memory tally and less moving bytes from pages than a physical integers table.
The questions that arise now are, does COLUMNSTORE vs COLUMNSTORE_ARCHIVE make any difference in performance? Does the performance benefit go away relative to the other solutions when the number of integers needed is really low? (getting the first few rows out of a columnstore can be slower than getting the first few rows out of heaps for some workloads)
FYI: Regular columnstore vs archive made it go slower
–GetNumsJohn2 (archive compression 1.6MB)
––CPU time = 20563 ms, elapsed time = 20755 ms.
–GetNumsJohn2 (columnstore compression 2.89MB)
–CPU time = 23454 ms, elapsed time = 26591 ms.
John, thanks for posting this!
@John Number2, that is a good solution.
Wonder what happens if you create a smaller CCI of 32768 and cross join it.
Charlie, I had similar thoughts. :) Though I used a table with 65,536 rows so that with a single cross join you would get 4B rows.
It's slower than John's single table approach by ~ 22.6%, but it has the advantage of instantaneous population of the physical table.
Amazingly, the table sizes on disk are almost the same in both cases (~ 1 – 1.6 MB) because of the compression used by columnstore, which uses one entry for repeated occurrences of the same value along with the count of occurrences. Joe's table is ~ 350 MB.
In this test, I used Alan's approach with the variable assignment to eliminate the async network I/O waits.
Here's the test with Joe's solution:
Insertion time: 1:04 minutes.
Table size: ~ 350 MB
— CPU time = 4969 ms, elapsed time = 4982 ms.
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsObbish(1, 100000000);
GO
— Adding order
— CPU time = 44516 ms, elapsed time = 34836 ms.
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsObbish(1, 100000000) ORDER BY n;
It's blazing fast when ordering is not needed, but requires a sort when order is needed, which results in a big performance penalty.
Here's John's function (including the ideas from John, Dave, Joe, Alan, Charlie, Itzik):
DROP TABLE IF EXISTS dbo.NullBits4B;
GO
CREATE TABLE dbo.NullBits4B
(
b BIT NULL,
INDEX cc_NullBits4B CLUSTERED COLUMNSTORE
WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE)
);
GO
— 12:32 minutes insertion time
WITH
L0 AS (SELECT CAST(NULL AS BIT) AS b
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B),
L2 AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B),
nulls(b) AS (SELECT A.b FROM L2 AS A CROSS JOIN L2 AS B)
INSERT INTO dbo.NullBits4B WITH (TABLOCK) (b)
SELECT b FROM nulls;
GO
— ~ 1.64 MB
EXEC sys.sp_spaceused @objname = N'dbo.NullBits4B';
GO
CREATE OR ALTER FUNCTION dbo.GetNumsJohn2DaveObbishAlanCharlieItzik(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum FROM dbo.NullBits4B)
SELECT TOP(@high – @low + 1)
rownum AS rn,
@high + 1 – rownum AS op,
@low – 1 + rownum AS n
FROM Nums
ORDER BY rownum;
GO
— Test function's performance
— CPU time = 7593 ms, elapsed time = 7590 ms.
— Figure 5
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik(1, 100000000);
GO
— Adding order
— CPU time = 7578 ms, elapsed time = 7582 ms.
— Same plan as in Figure 5
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik(1, 100000000) ORDER BY n;
GO
It's slower than Joe's solution when no order is needed, but performs exactly the same when order is needed since there's no sort. Table size is very small. The main issue is insertion time of the table, though this happens only once.
Here's the revision with the 65,536-row table and the cross join:
DROP TABLE IF EXISTS dbo.NullBits65536;
GO
CREATE TABLE dbo.NullBits65536
(
b BIT NULL,
INDEX cc_NullBits65536 CLUSTERED COLUMNSTORE
WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE)
);
GO
— 91 ms
WITH
L0 AS (SELECT CAST(NULL AS BIT) AS b
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B),
nulls(b) AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B)
INSERT INTO dbo.NullBits65536 WITH (TABLOCK) (b)
SELECT b FROM nulls;
GO
— ~ 0.9 MB
EXEC sys.sp_spaceused @objname = N'dbo.NullBits65536';
GO
CREATE OR ALTER FUNCTION dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM dbo.NullBits65536 AS A CROSS JOIN dbo.NullBits65536 AS B)
SELECT TOP(@high – @low + 1)
rownum AS rn,
@high + 1 – rownum AS op,
@low – 1 + rownum AS n
FROM Nums
ORDER BY rownum;
GO
— Test function's performance
— CPU time = 9391 ms, elapsed time = 9390 ms.
— Figure 6
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);
GO
— Adding order
— CPU time = 9297 ms, elapsed time = 9303 ms.
— Same plan as in Figure 6
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) ORDER BY n OPTION(MAXDOP 1);
GO
As you can see, run time is ~ 22.6% longer. But it's still very fast! It also doesn't require a sort when order is needed. Also here the table size is tiny, with a negligible insertion time.
I'll cover these solutions next month.
I wonder if we can somehow inflate the table straight from bare pages.
What about inserting via BCP? What about loading in parallel? What about standard CCI compression?
Why does the smaller CCI even use 1.6MB, I would have thought it would be a single rowgroup?
Charlie, I believe that this has to do with the fact that in this architecture, a row group is limited to 2^20 rows. With 4B in the table, you get 4096 row groups.
select count(*) numrowgroups
from sys.column_store_row_groups
where object_id = object_id('dbo.NullBits4B');
With dbo.NullBits65536 you get only one row group.
select count(*) numrowgroups
from sys.column_store_row_groups
where object_id = object_id('dbo.NullBits65536');
Thank you! Just being able to be a part of this discussion with you lot is an honor.
Charlie, I wondered the same thing…like if there's only 1.6M of data in that thing once all the compression is done, my brain said there's gotta be a way to kind of raw copy the rowgroups from this to a file for quick import. I just didn't know enough about the internals to attempt that.
I did try a raw bulk copy using BCP and SSIS and of course it wants to stream row-by-row 10K rows at a time no matter what options I use. For some reason I had hoped that when it did a native copy it would just copy the pages involved…but when the coffee hit me and my brain woke up I remembered with CC tables, it's not really pages, is it…it's row groups.
Also of note, when MAXDOP was not specified during nullbits table creation, not only did it take longer, but it also was bigger (3.6M vs 1.6) and slower (24439 vs 20755)
Itzik, did you capture the IO profile of those options?
Itzik, I noticed you didn't use OPTION(MAXDOP 1) when you did
GetNumsJohn2DaveObbishAlanCharlieItzik
It performs considerably better on my machine when you do
Fun fact, I dropped the time it takes to insert 4B rows into NullBits from 20 minutes on my laptop to 7 minutes using OSTRESS.EXE to insert 16 separate connections of 2^20 rows (each one is a completely full rowgroup) x128 times. So instead of inserting at 10% CPU, it was inserting at ~ 100% CPU.
The one downside, the size of the table went from 1.6M to 2.3M, but I can't tell that any other performance characteristics have changed
In case someone wants the ostress commandline
ostress -S(local)\SQL2019STD -E -dnable -n32 -r128 -Q"WITH L0 AS (SELECT CAST(NULL AS BIT) AS b FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)), L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B), L2 AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B), nulls(b) AS (SELECT A.b FROM L2 AS A CROSS JOIN L2 AS B) INSERT INTO dbo.NullBits4B(b) SELECT TOP(1048576) b FROM nulls OPTION(MAXDOP 1);"
John,
Regarding why I didn't use MAXDOP 1, on my machine the parallel option was faster (12:32 minutes vs. 15:17 minutes).
Nice to see that your solution with the 16 separate connections made such a big difference.
As for the I/O profile of the solutions; yes, I captured those:
dbo.GetNumsObbish: 32928 lob logical reads
dbo.GetNumsJohn2DaveObbishAlanCharlieItzik: 194 lob logical reads
dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2: 119 logical reads
Oh, I meant why didn't you use maxdop 1 when running the function, not filling the table
John,
I didn't use MAXDOP 1 with GetNumsJohn2DaveObbishAlanCharlieItzik since I got a serial plan by default. I tested it emulating 2 to 32 CPUs and still always got a serial plan. So there was no need for the hint. Are you getting a parallel plan by default?
Oh, I see…actually, when I looked at it, I wasn't thinking serial vs parallel, but it absolutely is both ways. My origincal performance comparisons showed with MAXDOP 1 was a second faster, but now that I think back, I'm thinking the first run without was on a clean build, the second with maxdop 1 would have been with pre-cached results, hence the perceived performance increase.
But you're right, I see serial, so it's not needed. Thanks for the clarification. This is fun stuff
Fun fact:
To understand how truly huge a BIGINT is compared to an INT…
If we were to perform this same process, but use the maximums of BIGINT instead of INT (18446744073709551616 instead of 4294967296)
We would need to perform that insert of 4294967296 rows (which takes 2 minutes on my server, fully parallelized using ostress) exactly 4294967296 times.
So, 2 minutes * 4294967296 = 16,343 years. That's how long it would take to finish inserting the null bits into the table. And event with archival compression of empty bits it would still be 6.5536 Petabytes Yeah, I thought about it for a second…I have the disk space, I don't have the time :)
John, that's really mind-blowing. Although with a signed bigint you would "only" need to go up to 2^63 – 1 = 9223372036854775807. ;)
Still the number is huge. Obviously, a cross join would be the preferred method of choice.
Well, I thought 18 bazillion instead of 9 for the same reason we went up to 4294967296 instead of 2147483647 for your challenge, it would cover all the negatives as well as all the positives. but yeah, cross join is the way
Itzik, I was thinking about the cross join you're doing with 65536 rows…I get that you're choosing that number so that it's a perfect 4294967296 rows when crossjoined…but I wonder if it'd actually make more sense to use 1048576 so that it's a full row group that gets closed off and compressed.
–YOUR CROSS-JOIN OF 65536 ROWS
DROP TABLE IF EXISTS dbo.NullBits65536;
GO
CREATE TABLE dbo.NullBits65536
(
b BIT NULL,
INDEX cc_NullBits65536 CLUSTERED COLUMNSTORE
WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE)
);
GO
WITH
L0 AS (SELECT CAST(NULL AS BIT) AS b
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B),
nulls(b) AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B)
INSERT INTO dbo.NullBits65536 WITH (TABLOCK) (b)
SELECT b FROM nulls;
GO
— *** RESERVED 1168KB, DATA 928K, INDEX_SIZE 16K, UNUSED 224K ***
EXEC sys.sp_spaceused @objname = N'dbo.NullBits65536';
GO
–THE SAME THING, ONLY 1048576 ROWS
DROP TABLE IF EXISTS dbo.NullBits1048576;
GO
CREATE TABLE dbo.NullBits1048576
(
b BIT NULL,
INDEX cc_NullBits1048576 CLUSTERED COLUMNSTORE
WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE)
);
GO
WITH
L0 AS (SELECT CAST(NULL AS BIT) AS b
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B),
L2 AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B),
nulls(b) AS (SELECT A.b FROM L2 AS A CROSS JOIN L2 AS B)
INSERT INTO dbo.NullBits1048576 (b)
SELECT TOP(1048576) b FROM nulls OPTION(MAXDOP 1);
GO
— *** RESERVED 200KB, DATA 32KB, INDEX_SIZE 0KB, UNUSED 168KB ***
EXEC sys.sp_spaceused @objname = N'dbo.NullBits1048576';
GO
–65K rows
–944 KB (data+index)
–4 ms (compile time, goes to 0ms after rerun)
–24531 ms (cpu time)
–25166 ms (elapsed time)
–Scan count 4
–logical reads 120
–physical reads 0
–read-ahead reads 0
–lob logical reads 0
–lob physical reads 0
–lob read-ahead reads 0
–1048576 rows
–32 KB (data+index)
–2 ms (compile time, goes to 0ms after rerun)
–23875 ms (cpu time)
–24030 ms (elapsed time)
–Scan count 2
–logical reads 0
–physical reads 0
–read-ahead reads 0
–lob logical reads 8
–lob physical reads 0
–lob read-ahead reads 0.
–Segment reads 2
–segment skipped 0.
In other words, when less than 1048576 rows are inserted, it's an unclosed row group and it looks and acts kinda like a heap with 65535 rows to me. But when you have a full 1M rows, the rowgroup closes off and gets compressed. Still instantaneous loading of the table, but less compile time, less IO, less CPU, less runtime, less bytes on disk.
ROWS | 65K | 1M
SIZE > | 944K | 32K
COMPILE > | 4ms | 2ms
CPU TIME > | 24,531ms | 23,875ms
ELAPSED TIME > | 25,166ms | 24,030
TBL LOAD TIME | 4 | 2
LOGICAL RDS > | 120 | 0
PHYSICAL RDS | 0 | 0
READ AHD RDS | 0 | 0
LOB LGCL RDS < | 0 | 8
LOB PHYS RDS | 0 | 0
PHYSICAL RDS | 0 | 0
LOB RD AHD RDS | 0 | 0
SEGMENT RDS < | 0 | 2
SEGMENT SKPD | 0 | 0
(interesting, it kinda ate my text in a weird way…let's try that again)
In other words, when less than 1048576 rows are inserted, it's an unclosed row group and it looks and acts kinda like a heap with 65535 rows to me. But when you have a full 1M rows, the rowgroup closes off and gets compressed. Still instantaneous loading of the table, but less compile time, less IO, less CPU, less runtime, less bytes on disk.
ROWS | 65K | 1M
SIZE | 944K | 32K
COMPILE | 4ms | 2ms
CPU TIME | 24,531ms | 23,875ms
ELAPSED TIME | 25,166ms | 24,030
TBL LOAD TIME | 123ms | 621ms
SCAN CT | 4 | 2
LOGICAL RDS | 120 | 0
PHYSICAL RDS | 0 | 0
READ AHD RDS | 0 | 0
LOB LGCL RDS | 0 | 8
LOB PHYS RDS | 0 | 0
PHYSICAL RDS | 0 | 0
LOB RD AHD RDS | 0 | 0
SEGMENT RDS | 0 | 2
SEGMENT SKPD | 0 | 0
John,
Regarding 18 bazillion instead of 9, this is mostly academic, but I'd imagine that the ROW_NUMBER FUNCTION itself would overflow once it exceeds 2^63-1, before you apply the computation that gives you the range between @low and @high. :)
John, regarding the the deltastore vs a compressed row group, I can't believe I missed this! Although you don't need 2^20 rows; suffice to populate it with a minimum of 102,400. So I'll update the solution for the article with this:
— 43 ms to populate
DROP TABLE IF EXISTS dbo.NullBits102400;
GO
CREATE TABLE dbo.NullBits102400
(
b BIT NULL,
INDEX cc_NullBits102400 CLUSTERED COLUMNSTORE
WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE)
);
GO
WITH
L0 AS (SELECT CAST(NULL AS BIT) AS b
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B),
nulls(b) AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B CROSS JOIN L1 AS C)
INSERT INTO dbo.NullBits102400 WITH (TABLOCK) (b)
SELECT TOP(102400) b FROM nulls;
GO
This reduces the size from ~1MB to 293 bytes! :)
I'll update the function with this:
CREATE OR ALTER FUNCTION dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2
(@low AS BIGINT = 1, @high AS BIGINT) RETURNS TABLE
AS
RETURN
WITH
Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM dbo.NullBits102400 AS A
CROSS JOIN dbo.NullBits102400 AS B)
SELECT TOP(@high – @low + 1)
rownum AS rn,
@high + 1 – rownum AS op,
@low – 1 + rownum AS n
FROM Nums
ORDER BY rownum;
GO
I can't say I managed to measure any noticeable difference in run time, but that's certainly an improved version, and the I/Os drop to 8 lob logical reads. :)
Nice catch!
Doh, I had spaced the lower requirement for moving from delta to rowgroup. Had 2^20 on the brain from the earlier discussion on why it was even 1.6MB in the first place.
Regarding the BIGINT overflow, fair enough…it's all academic since the scale is so monumentally large so as to render it an impossible exercise anyway.
Dunno what it is about this particular series, but this whole discussion is all super interesting to me. Meanwhile, my wife is rolling her eyes.
John, same here, on both counts. ;)
Late to the party here, but I sure am glad I stumbled across this!! LOTS to be learned and put in my toolbox.
As soon as people mentioned CCIs and started populating them the first thing I thought of was "wait, you aren't putting the data in as 1M row batches". Then someone did 1M row batches – but concurrently. :-) Glad to see that finally got sorted.
I am off to read the rest of the series now, and cannot WAIT to see the final results! This reminds me of the several INCREDIBLE flurries of work the community did over the course of several years on Jeff Moden's tally/string split stuff on SQLServerCentral.com!
I found it interesting to look at exactly why the performance for the recursive CTE approach to this problem is so poor (if anyone else is interested! https://stackoverflow.com/a/70500904/73226)
Hi Martin,
It is indeed very interesting!