Last month I posted a challenge to create an efficient number series generator. The responses were overwhelming. There were many brilliant ideas and suggestions, with lots of applications well beyond this particular challenge. It made me realize how great it is to be part of a community, and that amazing things can be achieved when a group of smart people joins forces. Thanks Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason and John Number2 for sharing your ideas and comments.
Initially I thought of writing just one article to summarize the ideas people submitted, but there were too many. So I’ll split the coverage to several articles. This month I’ll focus primarily on Charlie’s and Alan Burstein’s suggested improvements to the two original solutions that I posted last month in the form of the inline TVFs called dbo.GetNumsItzikBatch and dbo.GetNumsItzik. I’ll name the improved versions dbo.GetNumsAlanCharlieItzikBatch and dbo.GetNumsAlanCharlieItzik, respectively.
This is so exciting!
Itzik’s original solutions
As a quick reminder, the functions I covered last month use a base CTE that defines a table value constructor with 16 rows. The functions use a series of cascading CTEs, each applying a product (cross join) of two instances of its preceding CTE. This way, with five CTEs beyond the base one, you can get a set of up to 4,294,967,296 rows. A CTE called Nums uses the ROW_NUMBER function to produce a series of numbers starting with 1. Finally, the outer query computes the numbers in the requested range between the inputs @low and @high.
The dbo.GetNumsItzikBatch function uses a dummy join to a table with a columnstore index to get batch processing. Here’s the code to create the dummy table:
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
And here’s the code defining the dbo.GetNumsItzikBatch function:
CREATE OR ALTER FUNCTION dbo.GetNumsItzikBatch(@low AS BIGINT, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum;
I used the following code to test the function with "Discard results after execution" enabled in SSMS:
SELECT n FROM dbo.GetNumsItzikBatch(1, 100000000) OPTION(MAXDOP 1);
Here are the performance stats that I got for this execution:
CPU time = 16985 ms, elapsed time = 18348 ms.
The dbo.GetNumsItzik function is similar, only it doesn’t have a dummy join, and normally gets row mode processing throughout the plan. Here’s the function’s definition:
CREATE OR ALTER FUNCTION dbo.GetNumsItzik(@low AS BIGINT, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum;
Here’s the code I used to test function:
SELECT n FROM dbo.GetNumsItzik(1, 100000000) OPTION(MAXDOP 1);
Here are the performance stats that I got for this execution:
CPU time = 19969 ms, elapsed time = 21229 ms.
Alan Burstein's and Charlie's improvements
Alan and Charlie suggested several improvements to my functions, some with moderate performance implications and some with more dramatic ones. I’ll start with Charlie’s findings regarding compilation overhead and constant folding. I’ll then cover Alan’s suggestions, including 1-based versus @low-based sequences (also shared by Charlie and Jeff Moden), avoiding unnecessary sort, and computing a numbers range in opposite order.
Compilation time findings
As Charlie noted, a number series generator is often used to generate series with very small numbers of rows. In those cases, the compile time of the code can become a substantial part of the total query processing time. That’s especially important when using iTVFs, since unlike with stored procedures, it’s not the parameterized query code that gets optimized, rather the query code after parameter embedding takes place. In other words, the parameters are substituted with the input values prior to optimization, and the code with the constants gets optimized. This process can have both negative and positive implications. One of the negative implications is that you get more compilations as the function is called with different input values. For this reason, compile times should definitely be taken into account—especially when using the function very frequently with small ranges.
Here are the compilation times Charlie found for the various base CTE cardinalities:
2: 22ms 4: 9ms 16: 7ms 256: 35ms
It’s curious to see that among these, 16 is the optimal, and that there’s a very dramatic jump when you go up to the next level, which is 256. Recall that the functions dbo.GetNumsItzikBacth and dbo.GetNumsItzik use base CTE cardinality of 16.
Constant folding
Constant folding is often a positive implication that in the right conditions may be enabled thanks to the parameter embedding process that an iTVF experiences. For example, suppose that your function has an expression @x + 1, where @x is an input parameter of the function. You invoke the function with @x = 5 as input. The inlined expression then becomes 5 + 1, and if eligible for constant folding (more on this shortly), then becomes 6. If this expression is part of a more elaborate expression involving columns, and is applied to many millions of rows, this can result in nonnegligible savings in CPU cycles.
The tricky part is that SQL Server is very picky about what to constant fold and what to not constant fold. For example, SQL Server will not constant fold col1 + 5 + 1, nor will it fold 5 + col1 + 1. But it will fold 5 + 1 + col1 to 6 + col1. I know. So, for example, if your function returned SELECT @x + col1 + 1 AS mycol1 FROM dbo.T1, you could enable constant folding with the following small alteration: SELECT @x + 1 + col1 AS mycol1 FROM dbo.T1. Don’t believe me? Examine the plans for the following three queries in the PerformanceV5 database (or similar queries with your data) and see for yourself:
SELECT orderid + 5 + 1 AS myorderid FROM dbo.orders;
SELECT 5 + orderid + 1 AS myorderid FROM dbo.orders;
SELECT 5 + 1 + orderid AS myorderid FROM dbo.orders;
I got the following three expressions in the Compute Scalar operators for these three queries, respectively:
[Expr1003] = Scalar Operator([PerformanceV5].[dbo].[Orders].[orderid]+(5)+(1)) [Expr1003] = Scalar Operator((5)+[PerformanceV5].[dbo].[Orders].[orderid]+(1)) [Expr1003] = Scalar Operator((6)+[PerformanceV5].[dbo].[Orders].[orderid])
See where I’m going with this? In my functions I used the following expression to define the result column n:
@low + rownum - 1 AS n
Charlie realized that with the following small alteration, he can enable constant folding:
@low - 1 + rownum AS n
For example, the plan for the earlier query that I provided against dbo.GetNumsItzik, with @low = 1, originally had the following expression defined by the Compute Scalar operator:
[Expr1154] = Scalar Operator((1)+[Expr1153]-(1))
After applying the above minor change, the expression in the plan becomes:
[Expr1154] = Scalar Operator((0)+[Expr1153])
That’s brilliant!
As for the performance implications, recall that the performance statistics that I got for the query against dbo.GetNumsItzikBatch before the change were the following:
CPU time = 16985 ms, elapsed time = 18348 ms.
Here are the numbers I got after the change:
CPU time = 16375 ms, elapsed time = 17932 ms.
Here are the numbers that I got for the query against dbo.GetNumsItzik originally:
CPU time = 19969 ms, elapsed time = 21229 ms.
And here are the numbers after the change:
CPU time = 19266 ms, elapsed time = 20588 ms.
Performance improved just a bit by a few percent. But wait, there’s more! If you need to process the data ordered, the performance implications can be much more dramatic, as I’ll get to later in the section about ordering.
1-based versus @low-based sequence and opposite row numbers
Alan, Charlie and Jeff noted that in the vast majority of the real-life cases where you need a range of numbers, you need it to start with 1, or sometimes 0. It’s far less common to need a different starting point. So it could make more sense to have the function always return a range that starts with, say, 1, and when you need a different starting point, apply any computations externally in the query against the function.
Alan actually came up with an elegant idea to have the inline TVF return both a column that starts with 1 (simply the direct result of the ROW_NUMBER function) aliased as rn, and a column that starts with @low aliased as n. Since the function gets inlined, when the outer query interacts only with the column rn, the column n doesn’t even get evaluated, and you get the performance benefit. When you do need the sequence to start with @low, you interact with the column n and pay the applicable extra cost, so there’s no need to add any explicit external computations. Alan even suggested adding a column called op that computes the numbers in opposite order, and interact with it only when in need for such a sequence. The column op is based on the computation: @high + 1 – rownum. This column has significance when you need to process the rows in descending number ordering as I demonstrate later in the ordering section.
So, let’s apply Charlie’s and Alan’s improvements to my functions.
For the batch mode version, make sure that you create the dummy table with the columnstore index first, if it’s not already present:
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
Then use the following definition for the dbo.GetNumsAlanCharlieItzikBatch function:
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1)
rownum AS rn,
@high + 1 - rownum AS op,
@low - 1 + rownum AS n
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum;
Here’s an example for using the function:
SELECT *
FROM dbo.GetNumsAlanCharlieItzikBatch(-2, 3) AS F
ORDER BY rn;
This code generates the following output:
rn op n --- --- --- 1 3 -2 2 2 -1 3 1 0 4 0 1 5 -1 2 6 -2 3
Next, test the function’s performance with 100M rows, first returning the column n:
SELECT n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
Here are the performance statistics that I got for this execution:
CPU time = 16375 ms, elapsed time = 17932 ms.
As you can see, there’s a small improvement compared to dbo.GetNumsItzikBatch in both CPU and elapsed time thanks to the constant folding that took place here.
Test the function, only this time returning the column rn:
SELECT rn FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
Here are the performance statistics that I got for this execution:
CPU time = 15890 ms, elapsed time = 18561 ms.
CPU time further reduced, though elapsed time seems to have increased a bit in this execution compared to when querying the column n.
Figure 1 has the plans for both queries.
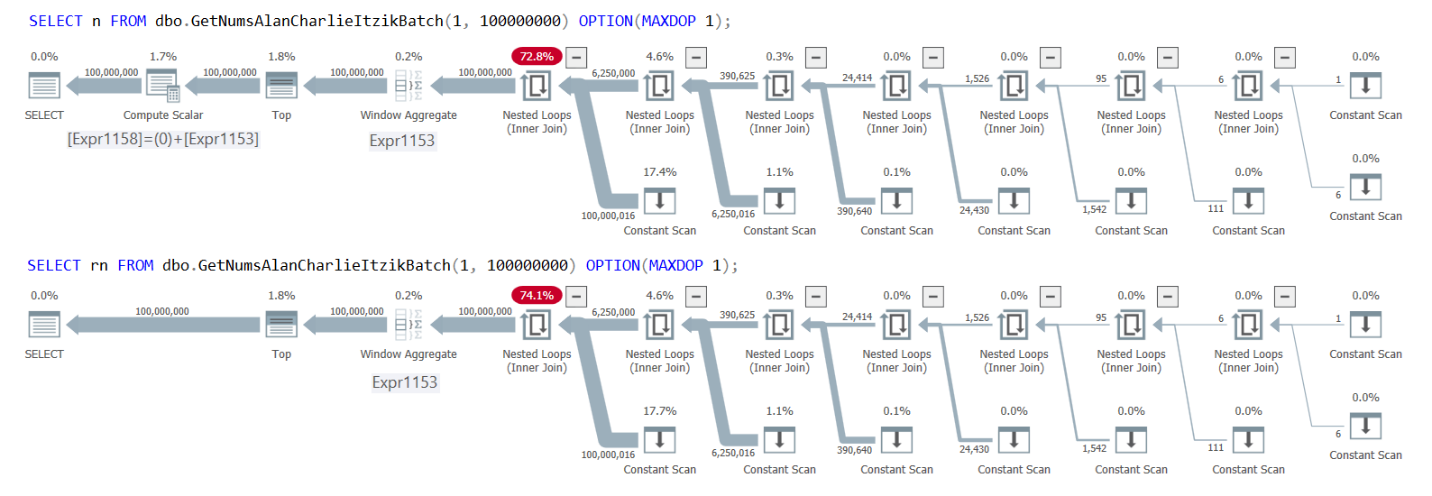 Figure 1: Plans for GetNumsAlanCharlieItzikBatch returning n versus rn
Figure 1: Plans for GetNumsAlanCharlieItzikBatch returning n versus rn
You can clearly see in the plans that when interacting with the column rn, there’s no need for the extra Compute Scalar operator. Also notice in the first plan the outcome of the constant folding activity that I described earlier, where @low – 1 + rownum was inlined to 1 – 1 + rownum, and then folded into 0 + rownum.
Here’s the definition of the row-mode version of the function called dbo.GetNumsAlanCharlieItzik:
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzik(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1)
rownum AS rn,
@high + 1 - rownum AS op,
@low - 1 + rownum AS n
FROM Nums
ORDER BY rownum;
Use the following code to test the function, first querying the column n:
SELECT n FROM dbo.GetNumsAlanCharlieItzik(1, 100000000) OPTION(MAXDOP 1);
Here are the performance statistics that I got:
CPU time = 19047 ms, elapsed time = 20121 ms.
As you can see, it’s a bit faster than dbo.GetNumsItzik.
Next, query the column rn:
SELECT rn FROM dbo.GetNumsAlanCharlieItzik(1, 100000000) OPTION(MAXDOP 1);
The performance numbers further improve on both the CPU and the elapsed time fronts:
CPU time = 17656 ms, elapsed time = 18990 ms.
Ordering considerations
The aforementioned improvements are certainly interesting, and the performance impact is nonnegligible, but not very significant. A much more dramatic and profound performance impact can be observed when you need to process the data ordered by the number column. This could be as simple as needing to return the rows ordered, but is just as relevant for any order-based processing need, e.g., a Stream Aggregate operator for grouping and aggregation, a Merge Join algorithm for joining, and so forth.
When querying dbo.GetNumsItzikBatch or dbo.GetNumsItzik and ordering by n, the optimizer doesn’t realize that the underlying ordering expression @low + rownum – 1 is order-preserving with respect to rownum. The implication is a bit similar to that of a non-SARGable filtering expression, only with an ordering expression this results in an explicit Sort operator in the plan. The extra sort affects the response time. It also affects scaling, which typically becomes n log n instead of n.
To demonstrate this, query dbo.GetNumsItzikBatch, requesting the column n, ordered by n:
SELECT n
FROM dbo.GetNumsItzikBatch(1,100000000)
ORDER BY n
OPTION(MAXDOP 1);
I got the following performance stats:
CPU time = 34125 ms, elapsed time = 39656 ms.
The run time more than doubles compared to the test without the ORDER BY clause.
Test the dbo.GetNumsItzik function in a similar way:
SELECT n
FROM dbo.GetNumsItzik(1,100000000)
ORDER BY n
OPTION(MAXDOP 1);
I got the following numbers for this test:
CPU time = 52391 ms, elapsed time = 55175 ms.
Also here run time more than doubles compared to the test without the ORDER BY clause.
Figure 2 has the plans for both queries.
 Figure 2: Plans for GetNumsItzikBatch and GetNumsItzik ordering by n
Figure 2: Plans for GetNumsItzikBatch and GetNumsItzik ordering by n
In both cases you can see the explicit Sort operator in the plans.
When querying dbo.GetNumsAlanCharlieItzikBatch or dbo.GetNumsAlanCharlieItzik and ordering by rn the optimizer doesn’t need to add a Sort operator to the plan. So you could return n, but order by rn, and this way avoid a sort. What’s a bit shocking, though—and I mean it in a good way—is that the revised version of n which experiences constant folding, is order-preserving! It’s easy for the optimizer to realize that 0 + rownum is an order-preserving expression with respect to rownum, and thus avoid a sort.
Try it. Query dbo.GetNumsAlanCharlieItzikBatch, returning n, and ordering by either n or rn, like so:
SELECT n
FROM dbo.GetNumsAlanCharlieItzikBatch(1,100000000)
ORDER BY n -- same with rn
OPTION(MAXDOP 1);
I got the following performance numbers:
CPU time = 16500 ms, elapsed time = 17684 ms.
That’s of course thanks to the fact that there was no need for a Sort operator in the plan.
Run a similar test against dbo.GetNumsAlanCharlieItzik:
SELECT n
FROM dbo.GetNumsAlanCharlieItzik(1,100000000)
ORDER BY n -- same with rn
OPTION(MAXDOP 1);
I got the following numbers:
CPU time = 19546 ms, elapsed time = 20803 ms.
Figure 3 has the plans for both queries:
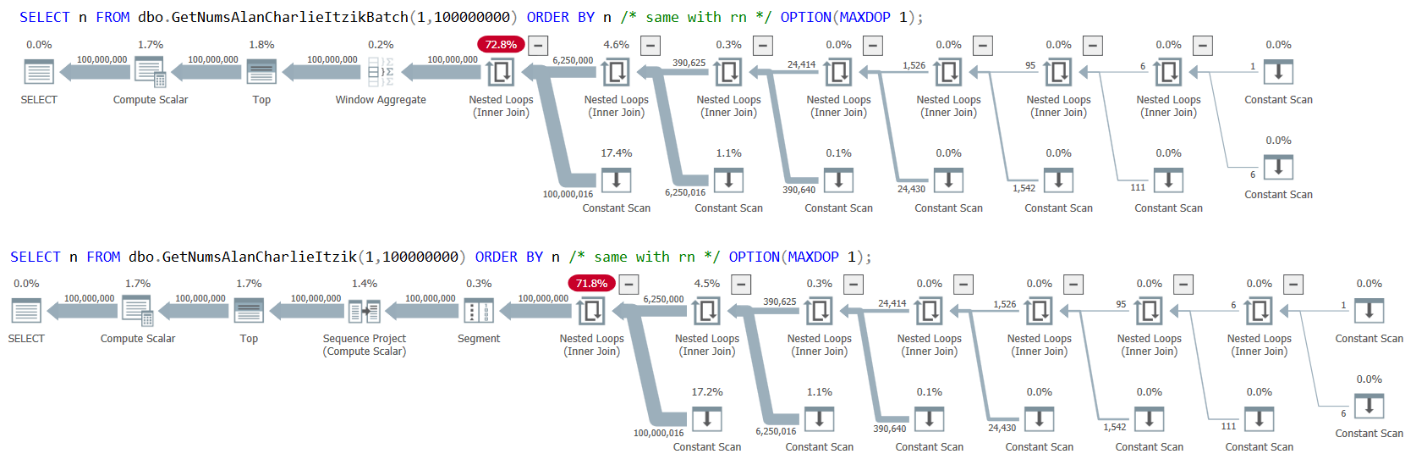
Figure 3: Plans for GetNumsAlanCharlieItzikBatch and GetNumsAlanCharlieItzik ordering by n or rn
Observe that there’s no Sort operator in the plans.
Makes you want to sing…
All you need is constant folding All you need is constant folding All you need is constant folding, constant folding Constant folding is all you need
Thank you Charlie!
But what if you need to return or process the numbers in descending order? The obvious attempt is to use ORDER BY n DESC, or ORDER BY rn DESC, like so:
SELECT n
FROM dbo.GetNumsAlanCharlieItzikBatch(1,100000000)
ORDER BY n DESC
OPTION(MAXDOP 1);
SELECT n
FROM dbo.GetNumsAlanCharlieItzikBatch(1,100000000)
ORDER BY rn DESC
OPTION(MAXDOP 1);
Unfortunately, though, both cases result in an explicit sort in the plans, as shown in Figure 4.
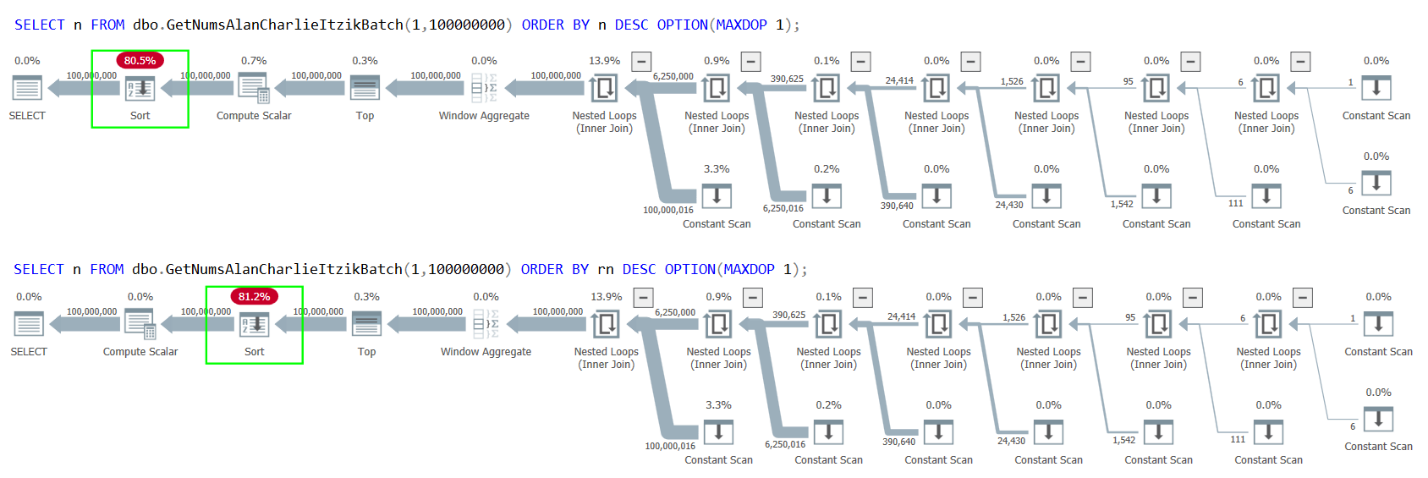 Figure 4: Plans for GetNumsAlanCharlieItzikBatch ordering by n or rn descending
Figure 4: Plans for GetNumsAlanCharlieItzikBatch ordering by n or rn descending
This is where Alan’s clever trick with the column op becomes a lifesaver. Return the column op while ordering by either n or rn, like so:
SELECT op
FROM dbo.GetNumsAlanCharlieItzikBatch(1,100000000)
ORDER BY n
OPTION(MAXDOP 1);
The plan for this query is shown in Figure 5.
 Figure 5: Plan for GetNumsAlanCharlieItzikBatch returning op and ordering by n or rn ascending
Figure 5: Plan for GetNumsAlanCharlieItzikBatch returning op and ordering by n or rn ascending
You get the data back ordered by n descending and there’s no need for a sort in the plan.
Thank you Alan!
Performance summary
So what have we learned from all of this?
Compilation times can be a factor, especially when using the function frequently with small ranges. On a logarithmic scale with a base 2, sweet 16 seems to be a nice magical number.
Understand the peculiarities of constant folding and use them to your advantage. When an iTVF has expressions that involve parameters, constants and columns, put the parameters and constants in the leading portion of the expression. This will increase the likelihood for folding, reduce CPU overhead, and increase the likelihood for order preservation.
It’s ok to have multiple columns that are used for different purposes in an iTVF, and query the relevant ones in each case without worrying about paying for the ones that aren’t referenced.
When you need the number sequence returned in opposite order, use the original n or rn column in the ORDER BY clause with ascending order, and return the column op, which computes the numbers in inverse order.
Figure 6 summarizes the performance numbers that I got in the various tests.
Next month I’ll continue exploring additional ideas, insights and solutions to the number series generator challenge.








Thank you, I'm honoured to be noted by the great Itzik!
Seriously, I think you've put more work into this than MS would have done even if they would actually given us a native 'fn_Tally'.
The constant-folding I picked from knowing a little about how compilers work. It's a shame SQL Server doesn't shuffle constants, most compilers do so. It also doesn't inline the obvious '0 + col'.
Please note, I didn't give those compilation time figures much thought, I hoped you would do further testing on more powerful hardware, more runs, larger amounts etc
חודש טוב
Charlie, thank you for sharing your ideas!
The performance tests in this article use the Discard results after execution option. They incur network async I/O waits since SQL Server does send the rows to SSMS; it's just that SSMS doesn't print them.
Here are the performance numbers that I got when testing the solutions using Alan's trick with the variable assignment:
Solution Row Mode Batch Mode
——————————– ————– ————
Itzik n 12.84 9.80
AlanCharlieItzik n 11.82 8.65
AlanCharlieItzik rn 10.72 7.32
Itzik n OrderBy n 42.50 23.57
AlanCharlieItzik n OrderBy n/rn 12.07 9.55
Next month??? :)
Never looked forward to a part 2,3…n more than I am now.
Hi Itzik.
I always apply calculations to the starting return value of 1 outside the function. I find the stuff about folding very interesting, especially how you avoided the sort operator.
I'm forced to wonder about the name check because the ITVF doesn't have WITH SCHEMABINDING on it. In your full battery of tests, does it make an appreciable difference?
Ed,
SCHEMABINDING has no performance impact in this case (I've tested it), although it might be a good idea to add it for other reasons.
It's certainly an option to apply the computations outside the function. The risk is that this could be done by a user who's unaware of the potential for breaking the order preservation property of the original ROW_NUMBER expression. Adding the computation inside the function, you can be sure to apply the order-preserving technique, making it transparent to the end user.
Just thinking: where @low is a small number and the number of rows is large, it's probably faster to do:
OFFSET @low ROWS
and skip the first one or two rows rather than adding
+ @low – 1
to *every* single row.
Another option we haven't considered, I shave off about 8% off the time:
Combined AS (
SELECT c = @low
UNION ALL
SELECT CAST(1 AS bigint)
FROM L3
),
Nums AS ( SELECT SUM(c) OVER(ORDER BY (SELECT NULL) ROWS UNBOUNDED PRECEDING) AS rownum
FROM Combined )
Admittedly the sum is perhaps non-deterministic as theoretically the UNION ALL could be reordered.
You then don't get the ordering guaranatee.
Might be solvable by calculating rownumber on the union first (over a sort column), then summing in order of the rownumber:
Combined AS (
SELECT c = @low, sortOrder = 1
UNION ALL
SELECT CAST(1 AS bigint), 2
FROM L3
),
Numbered AS (
SELECT c,
ROW_NUMBER() OVER (ORDER BY (SELECT NULL)) AS rn
FROM Combined
)
Nums AS ( SELECT SUM(c) OVER(ORDER BY rn ROWS UNBOUNDED PRECEDING) AS rownum
FROM Numbered )
Just occurred to me a feature we haven't considered at all, but is quite standard in procedural programming: an @step parameter.
In our row-numbering based solution, this can only be solved with multiplication of the row number.
Bu in my SUM method above, we can just replace CAST(1 AS bigint) with @step, this becomes an addition instead.
Must test the perf difference as multiplication is somewhat slower than addition on x86/x64 processors
Charlie, interesting ideas!
Regarding the one with the SUM OVER, I believe that even with your sort column, your current version is still nondeterministic. To make it deterministic, you would need to order by the sort column. Something like this (applying to the dbo.GetNumsAlanCharlieItzikBatch version):
CREATE OR ALTER FUNCTION dbo.CharliesAngel1(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Combined AS ( SELECT @low AS c, 1 AS sortorder
UNION ALL
SELECT CAST(1 AS BIGINT) AS c, 2 AS sortorder FROM L3 ),
Nums AS ( SELECT SUM(c) OVER(ORDER BY sortorder ROWS UNBOUNDED PRECEDING) AS rownum, sortorder
FROM Combined )
SELECT TOP(@high – @low + 1)
rownum AS n,
@low + @high – rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY sortorder;
GO
You would need to force a serial plan as well. My test:
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) ORDER BY n OPTION(MAXDOP 1);
I got 17.5 seconds, which is slower than the original, which took 9.5 seconds . Still, it's a very interesting idea!
Charlie, regarding a @step parameter, you're right. Would be interesting to experiment with different options. BTW, Alan Burstein has a version with multiplication here: https://codingblackarts.com/recommended-reading/using-rangeab-and-rangeab2/.
Of course, forgot to put in the actual sort column.
You're getting it wrong, the Combined sorts out the addition so you don't need to do it again, you can just do:
CREATE OR ALTER FUNCTION dbo.CharliesAngel1(@low AS BIGINT = 1, @high AS BIGINT, @step AS BIGINT = 1)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Combined AS (
SELECT @low AS c, 1 AS sortorder
UNION ALL
SELECT @step AS c, 2 AS sortorder
FROM L3
),
Nums AS (
SELECT TOP(@high – @low + 1)
SUM(c) OVER(ORDER BY sortorder ROWS UNBOUNDED PRECEDING) As n,
ROW_NUMBER() OVER (ORDER BY sortorder) AS rownum
FROM Combined
LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY sortorder
)
SELECT n, rownum
FROM Nums;
GO
I think the reason you're getting slower results is because you are ordering again by n, which I feel would rarely be necessary. Any case, ordering by rownum (which I have pulled out as an actual ROW_NUMBER) would give the correct ordering. I usually use this function for calendar or substring queries, and will be invariant to ordering.
Note: We can also get the reverse result by passing @step = -1
And if we have @step then logically we would have an @count not an @high
Charlie, this version has an expensive Merge Join (Concatenation) due to the ordering of the unified results, which is required buy both the running sum and the row number computation. This makes it slower than dbo.GetNumsAlanCharlieItzikBatch. Here are the time statistics I get for both:
— CPU time = 16047 ms, elapsed time = 16103 ms.
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.CharliesAngel1(1, 100000000, 1) OPTION(MAXDOP 1);
GO
— CPU time = 8969 ms, elapsed time = 9000 ms.
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
GO
So…it's next month…
:)
I know I'm late, but I only saw this now. This is my current version using the native function string_split. From my testing it was faster than any of the other variants.
create or alter function dbo.GetNumsStringSplit(@low bigint,@high bigint)
returns table
with schemabinding as
return
with t0 as (select n=value from string_split(space(255),' '))
,nums as (select rn= row_number() over (order by (select 1)) from t0 a,t0 b,t0 c, t0 d)
select top(@high – @low +1) rn = @low + rn – 1
from nums
Ooh, I like that idea! Use split to get the empty rowset…
Although, it doesn't seem to perform as well on my machine…
— 56,606 seconds
tvf_GetIntegersMichael(1,100000000) OPTION(MAXDOP 1);
–17,199 ms
tvf_GetIntegersMichael(1,100000000);
–8,607 ms
tvf_GetIntegersJohn2(1,100000000) OPTION(MAXDOP 1);
I also tried yours but using the cross join of 2 x 65535 rows instead of your 4 x 256…that one actually performed worse (I stopped it after 2 minutes)
And I tried something similar to yours only using OPENJSON() an an array of 256 0's and that one was 39seconds, so definitely slower too