Number series generator challenge solutions – Part 4

This is the fourth part in a series about solutions to the number series generator challenge. Many thanks to Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea and Paul White for sharing your ideas and comments.

I love Paul White’s work. I keep being shocked by his discoveries, and wonder how the heck he figures out what he does. I also love his efficient and eloquent writing style. Often while reading his articles or posts, I shake my head and tell my wife, Lilach, that when I grow up, I want to be just like Paul.

When I originally posted the challenge, I was secretly hoping that Paul would post a solution. I knew that if he did, it would be a very special one. Well, he did, and it’s fascinating! It has excellent performance, and there’s quite a lot that you can learn from it. This article is dedicated to Paul’s solution.

I’ll do my testing in tempdb, enabling I/O and time statistics:

SET NOCOUNT ON;

USE tempdb;

SET STATISTICS TIME, IO ON;

Limitations of earlier ideas

Evaluating earlier solutions, one of the important factors in getting good performance was the ability to employ batch processing. But have we exploited it to the maximum extent possible?

Let’s examine the plans for two of the earlier solutions that utilized batch processing. In Part 1 I covered the function dbo.GetNumsAlanCharlieItzikBatch, which combined ideas from Alan, Charlie and myself.

Here’s the function’s definition:

-- Helper dummy table
DROP TABLE IF EXISTS dbo.BatchMe;
GO

CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
GO

-- Function definition
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  WITH
    L0 AS ( SELECT 1 AS c
            FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
                        (1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
    L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
    L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
    L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
    Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
              FROM L3 )
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,

     @low - 1 + rownum AS n
  FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
  ORDER BY rownum;
GO

This solution defines a base table-value constructor with 16 rows, and a series of cascading CTEs with cross joins to inflate the number of rows to potentially 4B. The solution uses the ROW_NUMBER function to create the base sequence of numbers in a CTE called Nums, and the TOP filter to filter the desired number series cardinality. To enable batch processing, the solution uses a dummy left join with a false condition between the Nums CTE and a table called dbo.BatchMe, which has a columnstore index.

Use the following code to test the function with the variable assignment technique:

DECLARE @n AS BIGINT;

SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

The Plan Explorer depiction of the actual plan for this execution is shown in Figure 1.

Figure 1: Plan for dbo.GetNumsAlanCharlieItzikBatch function

When analyzing batch mode vs row mode processing, it’s quite nice to be able to tell just by looking at a plan at a high level which processing mode each operator used. Indeed, Plan Explorer shows a light blue batch figure at the bottom left part of the operator when its actual execution mode is Batch. As you can see in Figure 1, the only operator that used batch mode is the Window Aggregate operator, which computes the row numbers. There’s still a lot of work done by other operators in row mode.

Here are the performance numbers that I got in my test:

To identify which operators took most time to execute, either use the Actual Execution Plan option in SSMS, or the Get Actual Plan option in Plan Explorer. Make sure you read Paul’s recent article Understanding Execution Plan Operator Timings. The article describes how to normalize the reported operator execution times in order to get the correct numbers.

In the plan in Figure 1, most of the time is spent by the leftmost Nested Loops and Top operators, both executing in row mode. Besides row mode being less efficient than batch mode for CPU intensive operations, also, keep in mind that switching from row to batch mode and back takes extra toll.

In Part 2 I covered another solution that employed batch processing, implemented in the function dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2. This solution combined ideas from John Number2, Dave Mason, Joe Obbish, Alan, Charlie and myself. The main difference between the previous solution and this one is that as the base unit, the former uses a virtual table-value constructor and the latter uses an actual table with a columnstore index, giving you batch processing “for free.” Here’s the code that creates the table and populates it using an INSERT statement with 102,400 rows to get it to be compressed:

DROP TABLE IF EXISTS dbo.NullBits102400;
GO

CREATE TABLE dbo.NullBits102400
(
  b BIT NULL, 
  INDEX cc_NullBits102400 CLUSTERED COLUMNSTORE
    WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE)
);
GO

WITH
  L0 AS (SELECT CAST(NULL AS BIT) AS b
         FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
  L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B),
  nulls(b) AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B CROSS JOIN L1 AS C)
INSERT INTO dbo.NullBits102400 WITH (TABLOCK) (b) 
  SELECT TOP(102400) b FROM nulls;
GO

Here’s the function’s definition:

CREATE OR ALTER FUNCTION dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2
  (@low AS BIGINT = 1, @high AS BIGINT) RETURNS TABLE
AS
RETURN
  WITH
    Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
             FROM dbo.NullBits102400 AS A
               CROSS JOIN dbo.NullBits102400 AS B)
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
     @low - 1 + rownum AS n
  FROM Nums
  ORDER BY rownum;
GO

A single cross join between two instances of the base table is sufficient to produce well beyond the desired potential of 4B rows. Again here, the solution uses the ROW_NUMBER function to produce the base sequence of numbers and the TOP filter to restrict the desired number series cardinality.

Here’s the code to test the function using the variable assignment technique:

DECLARE @n AS BIGINT;

SELECT @n = n FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);

The plan for this execution is shown in Figure 2.

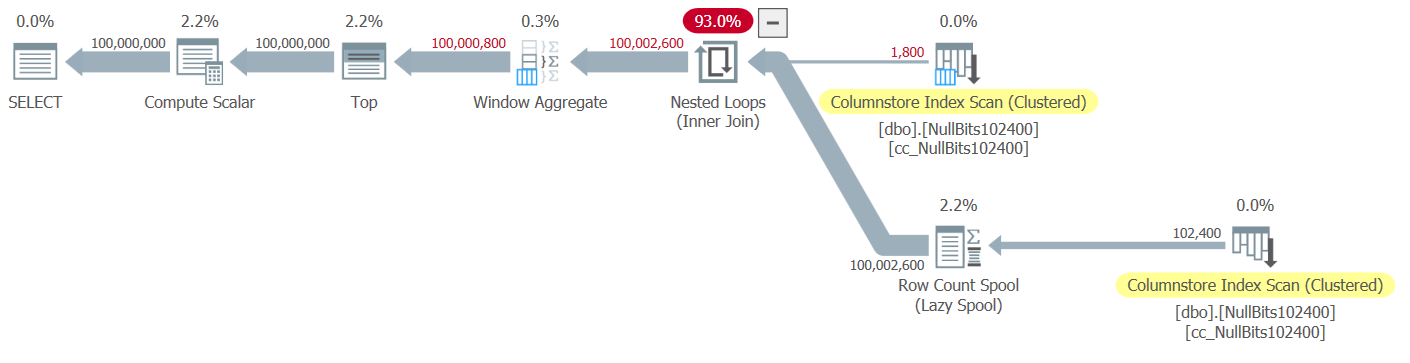Figure 2: Plan for dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2 function

Observe that only two operators in this plan utilize batch mode—the top scan of the table’s clustered columnstore index, which is used as the outer input of the Nested Loops join, and the Window Aggregate operator, which is used to compute the base row numbers.

I got the following performance numbers for my test:

Again, most of the time in the execution of this plan is spent by the leftmost Nested Loops and Top operators, which execute in row mode.

Paul’s solution

Before I present Paul’s solution, I’ll start with my theory regarding the thought process he went through. This is actually a great learning exercise, and I suggest that you go through it before looking at the solution. Paul recognized the debilitating effects of a plan that mixes both batch and row modes, and set a challenge to himself to come up with a solution that gets an all-batch-mode plan. If successful, the potential for such a solution to perform well is quite high. It’s certainly intriguing to see if such a goal is even attainable given that there are still many operators that don’t yet support batch mode and many factors that inhibit batch processing. For example, at the time of writing, the only join algorithm that supports batch processing is the hash join algorithm. A cross join is optimized using the nested loops algorithm. Furthermore, the Top operator is currently implemented only in row mode. These two elements are critical fundamental elements used in the plans for many of the solutions that I covered so far, including the above two.

Assuming that you gave the challenge to create a solution with an all-batch-mode plan a decent try, let’s proceed to the second exercise. I’ll first present Paul’s solution as he provided it, with his inline comments. I’ll also run it to compare its performance with the other solutions. I learned a great deal by deconstructing and reconstructing his solution, a step at a time, to make sure I carefully understood why he used each of the techniques that he did. I’ll suggest that you do the same before moving on to read my explanations.

Here’s Paul’s solution, which involves a helper columnstore table called dbo.CS and a function called dbo.GetNums_SQLkiwi:

-- Helper columnstore table
DROP TABLE IF EXISTS dbo.CS;
 
-- 64K rows (enough for 4B rows when cross joined)
-- column 1 is always zero
-- column 2 is (1...65536)
SELECT
    -- type as integer NOT NULL
    -- (everything is normalized to 64 bits in columnstore/batch mode anyway)
    n1 = ISNULL(CONVERT(integer, 0), 0), 
    n2 = ISNULL(CONVERT(integer, N.rn), 0)
INTO dbo.CS
FROM 
(
    SELECT
        rn = ROW_NUMBER() OVER (ORDER BY @@SPID)
    FROM master.dbo.spt_values AS SV1
    CROSS JOIN master.dbo.spt_values AS SV2
    ORDER BY 
        rn ASC
        OFFSET 0 ROWS
        FETCH NEXT 65536 ROWS ONLY
) AS N;
 
-- Single compressed rowgroup of 65,536 rows
CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS 
WITH (MAXDOP = 1);
GO

-- The function
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scala
        @low - 2 + N.rn < @high;
GO

Here’s the code I used to test the function with the variable assignment technique:

DECLARE @n AS BIGINT;

SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000);

I got the plan shown in Figure 3 for my test.

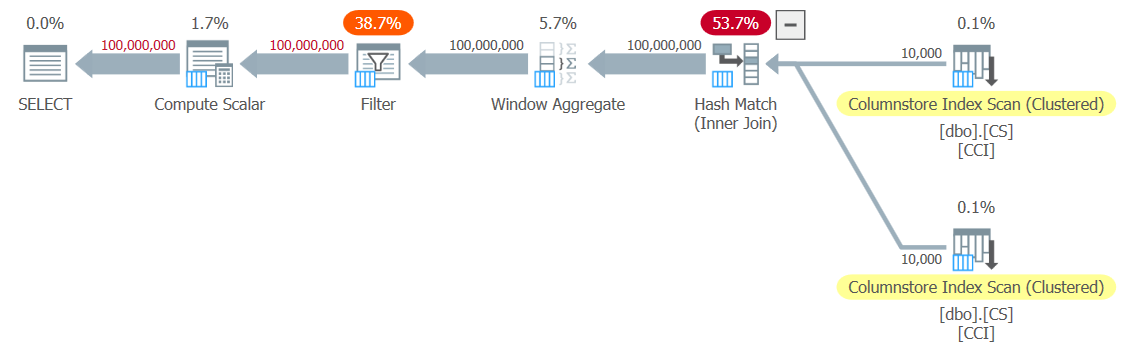Figure 3: Plan for dbo.GetNums_SQLkiwi function

It’s an all-batch-mode plan! That’s quite impressive.

Here are the performance numbers that I got for this test on my machine:

Let’s also verify that if you need to return the numbers ordered by n, the solution is order-preserving with respect to rn—at least when using constants as inputs—and thus avoid explicit sorting in the plan. Here’s the code to test it with order:

DECLARE @n AS BIGINT;

SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000) ORDER BY n;

You get the same plan as in Figure 3, and therefore similar performance numbers:

That’s an important side to the solution.

Changing our testing methodology

Paul’s solution’s performance is a decent improvement in both elapsed time and CPU time compared to the two previous solutions, but it doesn’t seem like the more dramatic improvement one would expect from an all-batch-mode plan. Perhaps we’re missing something?

Let’s try and analyze the operator execution times by looking at the Actual Execution Plan in SSMS as shown in Figure 4.

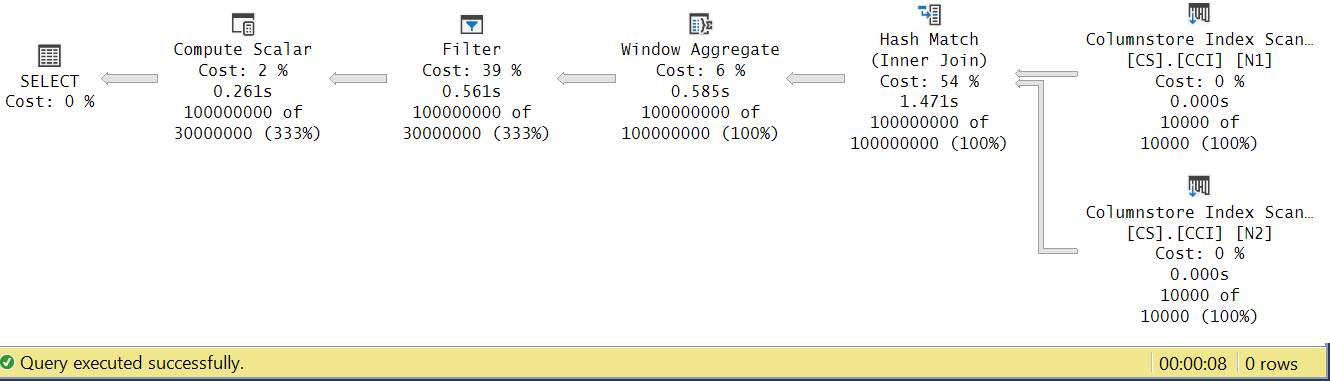Figure 4: Operator execution times for dbo.GetNums_SQLkiwi function

In Paul’s article about analyzing operator execution times he explains that with batch mode operators each reports its own execution time. If you sum the execution times of all operators in this actual plan, you’ll get 2.878 seconds, yet the plan took 7.876 to execute. 5 seconds of the execution time seem to be missing. The answer to this lies in the testing technique that we’re using, with the variable assignment. Recall that we decided to use this technique to eliminate the need to send all rows from the server to the caller and to avoid the I/Os that would be involved in writing the result to a table. It seemed like the perfect option. However, the true cost of the variable assignment is hidden in this plan, and of course, it executes in row mode. Mystery solved.

Obviously at the end of the day a good test is a test that adequately reflects your production use of the solution. If you typically write the data to a table, you need your test to reflect that. If you send the result to the caller, you need your test to reflect that. At any rate, the variable assignment seems to represent a big part of the execution time in our test, and clearly is unlikely to represent typical production use of the function. Paul suggested that instead of variable assignment the test could apply a simple aggregate like MAX to the returned number column (n/rn/op). An aggregate operator can utilize batch processing, so the plan would not involve conversion from batch to row mode as a result of its use, and its contribution to the total run time should be fairly small and known.

So let’s retest all three solutions covered in this article. Here’s the code to test the function dbo.GetNumsAlanCharlieItzikBatch:

SELECT MAX(n) AS mx FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

I got the plan shown in Figure 5 for this test.

Figure 5: Plan for dbo.GetNumsAlanCharlieItzikBatch function with aggregate

Here are the performance numbers that I got for this test:

Observe that run time dropped from 10.025 seconds using the variable assignment technique to 8.733 using the aggregate technique. That’s a bit over a second of execution time that we can attribute to the variable assignment here.

Here’s the code to test the function dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2:

SELECT MAX(n) AS mx FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);

I got the plan shown in Figure 6 for this test.

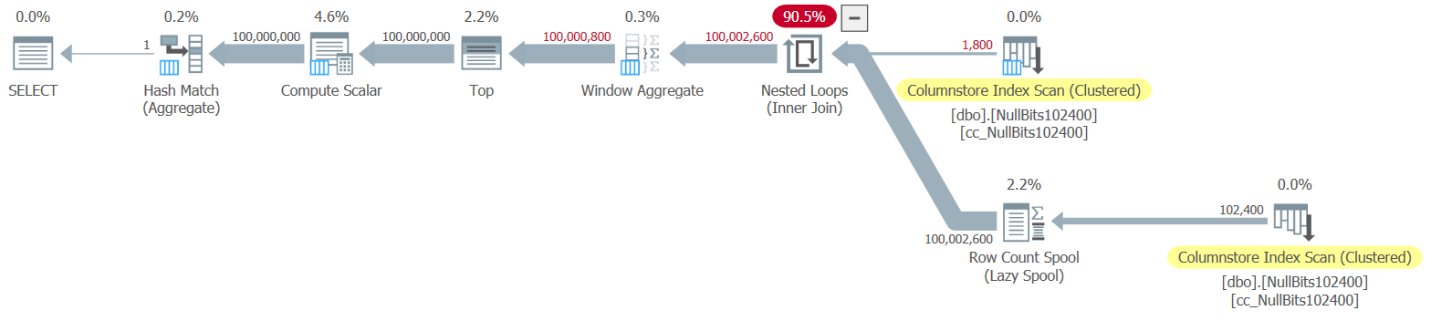Figure 6: Plan for dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2 function with aggregate

Here are the performance numbers that I got for this test:

Observe that run time dropped from 9.813 seconds using the variable assignment technique to 7.053 using the aggregate technique. That’s a bit over two seconds of execution time that we can attribute to the variable assignment here.

And here’s the code to test Paul’s solution:

SELECT MAX(n) AS mx FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(MAXDOP 1);

I get the plan shown in Figure 7 for this test.

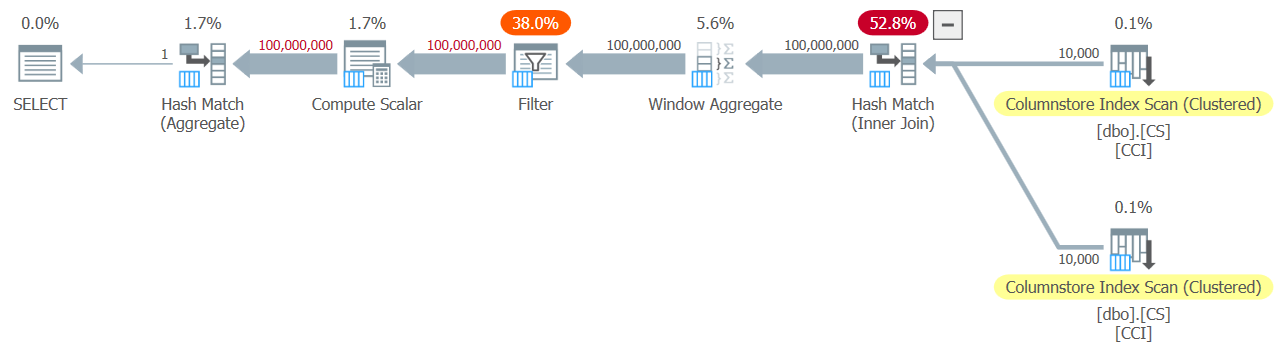Figure 7: Plan for dbo.GetNums_SQLkiwi function with aggregate

And now for the big moment. I got the following performance numbers for this test:

Run time dropped from 7.822 seconds to 3.149 seconds! Let’s examine the operator execution times in the actual plan in SSMS, as shown in Figure 8.

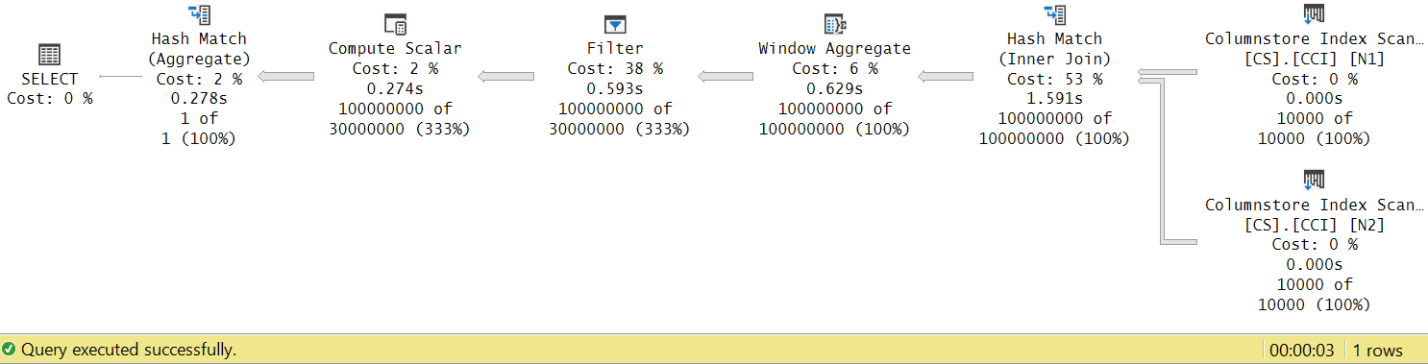Figure 8: Operator execution times for dbo.GetNums function with aggregate

Now if you accumulate the execution times of the individual operators you will get a similar number to the total plan execution time.

Figure 9 has a performance comparison in terms of elapsed time between the three solutions using both the variable assignment and aggregate testing techniques.

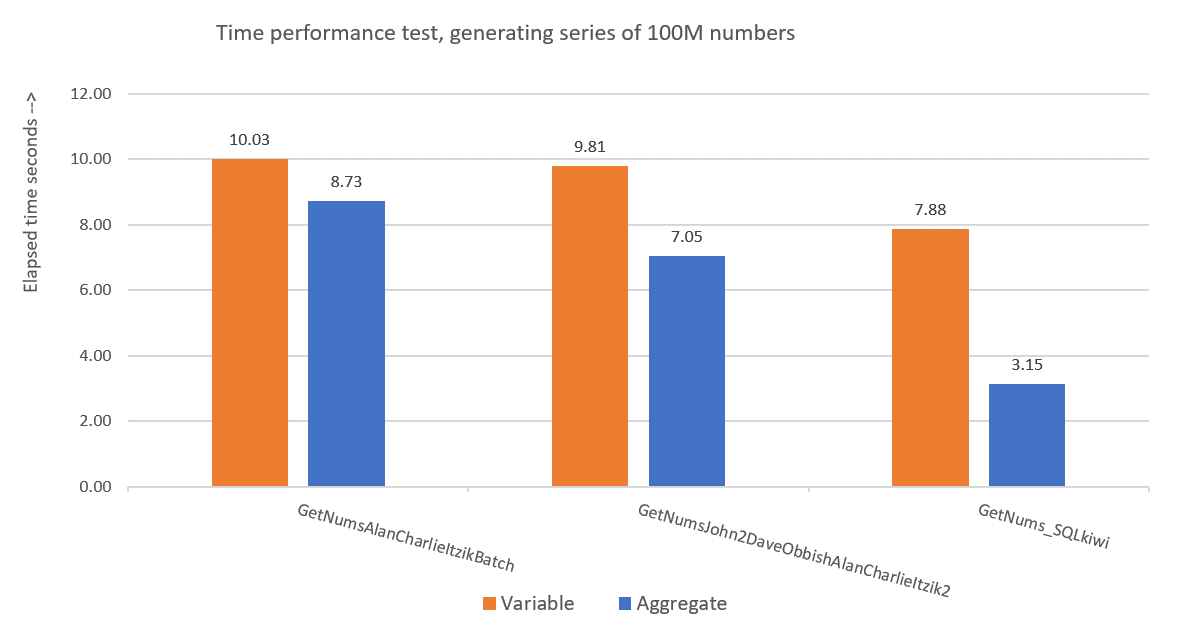Figure 9: Performance comparison

Paul’s solution is a clear winner, and this is especially apparent when using the aggregate testing technique. What an impressive feat!

Deconstructing and reconstructing Paul's solution

Deconstructing and then reconstructing Paul’s solution is a great exercise, and you get to learn a lot while doing so. As suggested earlier, I recommend that you go through the process yourself before you continue reading.

The first choice that you need to make is the technique that you would use to generate the desired potential number of rows of 4B. Paul chose to use a columnstore table and populate it with as many rows as the square root of the required number, meaning 65,536 rows, so that with a single cross join, you would get the required number. Perhaps you’re thinking that with fewer than 102,400 rows you would not get a compressed row group, but this applies when you populate the table with an INSERT statement like we did with the table dbo.NullBits102400. It doesn’t apply when you create a columnstore index on a prepopulated table. So Paul used a SELECT INTO statement to create and populate the table as a rowstore-based heap with 65,536 rows, and then created a clustered columnstore index, resulting in a compressed row group.

The next challenge is figuring out how to get a cross join to be processed with a batch mode operator. For this, you need the join algorithm to be hash. Remember that a cross join is optimized using the nested loops algorithm. You somehow need to trick the optimizer to think that you’re using an inner equijoin (hash requires at least one equality-based predicate), but get a cross join in practice.

An obvious first attempt is to use an inner join with an artificial join predicate that is always true, like so:

SELECT *
FROM dbo.CS AS N1
  INNER HASH JOIN dbo.CS AS N2
    ON 0 = 0;

But this code fails with the following error:

SQL Server’s optimizer recognizes that this is an artificial inner join predicate, simplifies the inner join to a cross join, and produces an error saying that it cannot accommodate the hint to force a hash join algorithm.

To solve this, Paul created an INT NOT NULL column (more on why this specification shortly) called n1 in his dbo.CS table, and populated it with 0 in all rows. He then used the join predicate N2.n1 = N1.n1, effectively getting the proposition 0 = 0 in all match evaluations, while complying with the minimal requirements for a hash join algorithm.

This works and produces an all-batch-mode plan:

SELECT *
FROM dbo.CS AS N1
  INNER HASH JOIN dbo.CS AS N2
    ON N2.n1 = N1.n1;

As for the reason for n1 to be defined as INT NOT NULL; why disallow NULLs, and why not use BIGINT? The reason for these choices is to avoid a hash probe residual (an extra filter that is applied by the hash join operator beyond the original join predicate), which could result in extra unnecessary cost. See Paul’s article Join Performance, Implicit Conversions, and Residuals for details. Here’s the part from the article that is relevant to us:

To check this aspect, let’s create another table called dbo.CS2 with a nullable n1 column:

DROP TABLE IF EXISTS dbo.CS2;

SELECT * INTO dbo.CS2 FROM dbo.CS;

ALTER TABLE dbo.CS2 ALTER COLUMN n1 INT NULL;

CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS2
WITH (MAXDOP = 1);

Let’s first test a query against dbo.CS (where n1 is defined as INT NOT NULL), generating 4B base row numbers in a column called rn, and applying the MAX aggregate to the column:

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS AS N1
    JOIN dbo.CS AS N2
        ON N2.n1 = N1.n1
) AS N;

We will compare the plan for this query with the plan for a similar query against dbo.CS2 (where n1 is defined as INT NULL):

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS2 AS N1
    JOIN dbo.CS2 AS N2
        ON N2.n1 = N1.n1
) AS N;

The plans for both queries are shown in Figure 10.

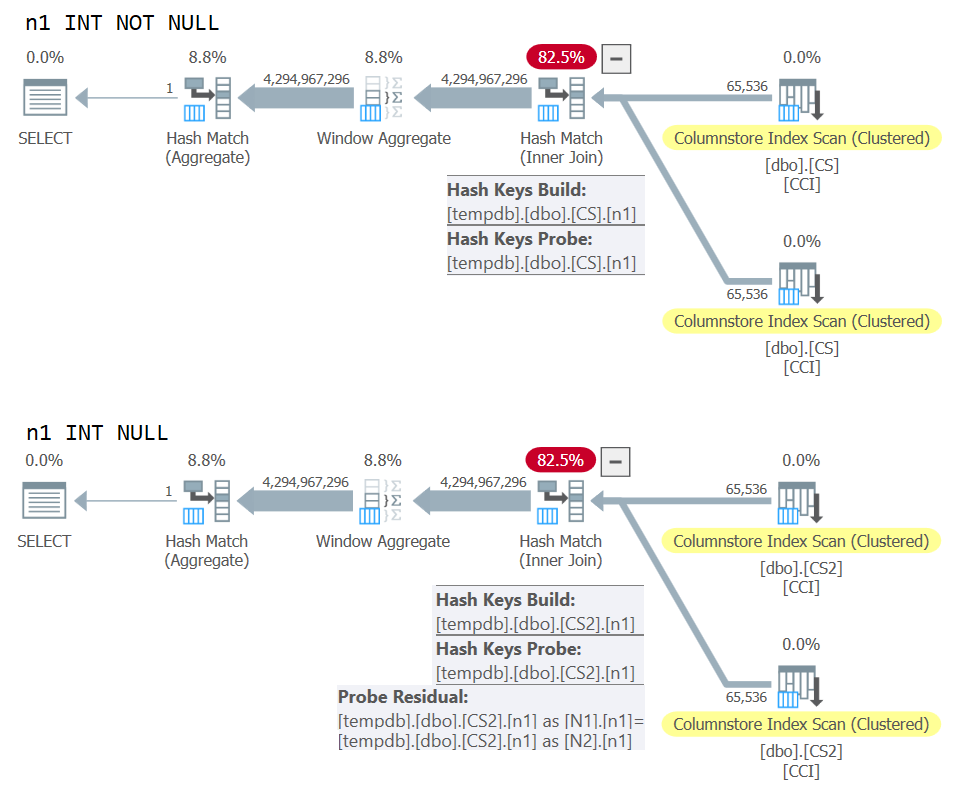Figure 10: Plan comparison for NOT NULL vs NULL join key

You can clearly see the extra probe residual that is applied in the second plan but not the first.

On my machine the query against dbo.CS completed in 91 seconds, and the query against dbo.CS2 completed in 92 seconds. In Paul’s article he reports an 11% difference in favor of the NOT NULL case for the example he used.

BTW, those of you with a keen eye will have noticed the use of ORDER BY @@TRANCOUNT as the ROW_NUMBER function’s ordering specification. If you carefully read Paul’s inline comments in his solution, he mentions that the use of the function @@TRANCOUNT is a parallelism inhibitor, whereas using @@SPID isn’t. So you can use @@TRANCOUNT as the run time constant in the ordering specification when you want to force a serial plan and @@SPID when you don’t.

As mentioned, it took the query against dbo.CS 91 seconds to run on my machine. At this point it could be interesting to test the same code with a true cross join, letting the optimizer use a row-mode nested loops join algorithm:

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS AS N1
    CROSS JOIN dbo.CS AS N2
) AS N;

It took this code 104 seconds to complete on my machine. So we do get a sizable performance improvement with the batch-mode hash join.

Our next problem is the fact that when using TOP to filter the desired number of rows, you get a plan with a row-mode Top operator. Here’s an attempt to implement the dbo.GetNums_SQLkiwi function with a TOP filter:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT TOP (100000000 - 1 + 1)
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        ORDER BY rn
    ) AS N;
GO

Let’s test the function:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

I got the plan shown in Figure 11 for this test.

Figure 11: Plan with TOP filter

Observe that the Top operator is the only one in the plan that uses row-mode processing.

I got the following time statistics for this execution:

The biggest part of the run time in this plan is spent by the row-mode Top operator and the fact that the plan needs to go through batch-to-row-mode conversion and back.

Our challenge is to figure out a batch-mode filtering alternative to the row-mode TOP. Predicate based filters like ones applied with the WHERE clause can potentially be handled with batch processing.

Paul’s approach was to introduce a second INT-typed column (see the inline comment “everything is normalized to 64-bit in columnstore/batch mode anyway”) called n2 to the table dbo.CS, and populate it with the integer sequence 1 through 65,536. In the solution’s code he used two predicate-based filters. One is a coarse filter in the inner query with predicates involving the column n2 from both sides of the join. This coarse filter can result in some false positives. Here’s the first simplistic attempt at such a filter:

WHERE
    -- Coarse filter:
    N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))

With the inputs 1 and 100,000,000 as @low and @high, you get no false positives. But try with 1 and 100,000,001, and you do get some. You’ll get a sequence of 100,020,001 numbers instead of 100,000,001.

To eliminate the false positives, Paul added a second, precise, filter involving the column rn in the outer query. Here’s the first simplistic attempt at such a precise filter:

WHERE
    -- Precise filter:
    N.rn < @high - @low + 2

Let’s revise the definition of the function to use the above predicate-based filters instead of TOP, take 1:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT
            rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        WHERE
            -- Coarse filter:
            N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    ) AS N
    WHERE
        -- Precise filter:
        N.rn < @high - @low + 2;
GO

Let’s test the function:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

I got the plan shown in Figure 12 for this test.

Figure 12: Plan with WHERE filter, take 1

Alas, something clearly went wrong. SQL Server converted our predicate-based filter involving the column rn to a TOP-based filter, and optimized it with a Top operator—which is exactly what we tried to avoid. To add insult to injury, the optimizer also decided to use the nested loops algorithm for the join.

It took this code 18.8 seconds to finish on my machine. Doesn’t look good.

Regarding the nested loops join, this is something that we could easily take care of using a join hint in the inner query. Just to see the performance impact, here’s a test with a forced hash join query hint used in the test query itself:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(HASH JOIN);

Run time reduces to 13.2 seconds.

We still have the issue with the conversion of the WHERE filter against rn to a TOP filter. Let’s try and understand how this happened. We used the following filter in the outer query:

WHERE N.rn < @high - @low + 2 

Remember that rn represents an unmanipulated ROW_NUMBER-based expression. A filter based on such an unmanipulated expression being in a given range is often optimized with a Top operator, which for us is bad news due to the use of row-mode processing.

Paul’s workaround was to use an equivalent predicate, but one that applies manipulation to rn, like so:

WHERE @low - 2 + N.rn < @high

Filtering an expression that adds manipulation to a ROW_NUMBER-based expression inhibits the conversion of the predicate-based filter to a TOP-based one. That’s brilliant!

Let’s revise the function’s definition to use the above WHERE predicate, take 2:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT
            rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        WHERE
            -- Coarse filter:
            N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    ) AS N
    WHERE
        -- Precise filter:
        @low - 2 + N.rn < @high;
GO

Test the function again, without any special hints or anything:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

It naturally gets an all-batch-mode plan with a hash join algorithm and no Top operator, resulting in an execution time of 3.177 seconds. Looking good.

The next step is to check if the solution handles bad inputs well. Let’s try it with a negative delta:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);

This execution fails with the following error.

Paul’s solution involved two additions. One is to add the following predicate to the inner query’s WHERE clause:

 @high >= @low

This filter does more than what it seems initially. If you’ve read Paul’s inline comments carefully, you could find this part:

The intriguing part here is the potential to use a constant scan with constants as inputs. I’ll get to this shortly.

The other addition is to apply the IIF function to the input expression to the SQRT function. This is done to avoid negative input when using nonconstants as inputs to our numbers function, and in case the optimizer decides to handle the predicate involving SQRT before the predicate @high >= @low.

Before the IIF addition, for example, the predicate involving N1.n2 looked like this:

N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))

After adding IIF, it looks like this:

N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))

With these two additions, we’re now basically ready for the final definition of the dbo.GetNums_SQLkiwi function:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scalar
        @low - 2 + N.rn < @high;
GO

Now back to the comment about the constant scan. When using constants that result in a negative range as inputs to the function, e.g., 100,000,000 and 1 as @low and @high, after parameter embedding the WHERE filter of the inner query looks like this:

WHERE
    1 >= 100000000
    AND ...

The whole plan can then be simplified to a single Constant Scan operator. Try it:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);

The plan for this execution is shown in Figure 13.

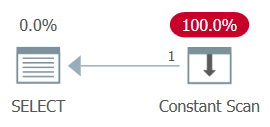Figure 13: Plan with constant scan

Unsurprisingly, I got the following performance numbers for this execution:

When passing a negative range with nonconstants as inputs, the use of the IIF function will prevent any attempt to compute a square root of a negative input.

Now let’s test the function with a valid input range:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

You get the all-batch-mode plan shown in Figure 14.

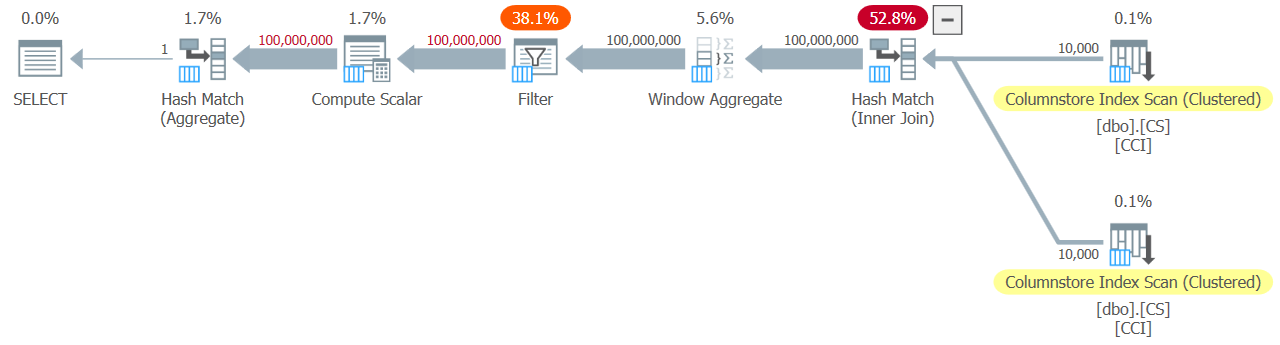Figure 14: Plan for dbo.GetNums_SQLkiwi function

This is the same plan you saw earlier in Figure 7.

I got the following time statistics for this execution:

Ladies and gentlemen, I think we have a winner! :)

Conclusion

I’ll have what Paul’s having.

Are we done yet, or is this series going to last forever?

No and no.