When SQL Server optimizes a query, during an exploration phase it produces candidate plans and chooses among them the one that has the lowest cost. The chosen plan is supposed the have the lowest run time among the explored plans. The thing is, the optimizer can only choose between strategies that were encoded into it. For instance, when optimizing grouping and aggregation, at the date of this writing, the optimizer can only choose between Stream Aggregate and Hash Aggregate strategies. I covered the available strategies in earlier parts in this series. In Part 1 I covered the preordered Stream Aggregate strategy, in Part 2 the Sort + Stream Aggregate strategy, in Part 3 the Hash Aggregate strategy, and in Part 4 parallelism considerations.
What the SQL Server optimizer currently doesn’t support is customization and artificial intelligence. That is, if you can figure out a strategy that under certain conditions is more optimal than the ones that the optimizer supports, you cannot enhance the optimizer to support it, and the optimizer cannot learn to use it. However, what you can do, is rewrite the query using alternative query elements that can be optimized with the strategy that you have in mind. In this fifth and last part in the series I demonstrate this technique of query tuning using query revisions.
Big thanks to Paul White (@SQL_Kiwi) for helping with some of the costing calculations presented in this article!
Like in the previous parts in the series, I’ll use the PerformanceV3 sample database. Use the following code to drop unneeded indexes from the Orders table:
DROP INDEX idx_nc_sid_od_cid ON dbo.Orders;
DROP INDEX idx_unc_od_oid_i_cid_eid ON dbo.Orders;
Default optimization strategy
Consider the following basic grouping and aggregation tasks:
Return the maximum order date for each shipper, employee, and customer.
For optimal performance, you create the following supporting indexes:
CREATE INDEX idx_sid_od ON dbo.Orders(shipperid, orderdate);
CREATE INDEX idx_eid_od ON dbo.Orders(empid, orderdate);
CREATE INDEX idx_cid_od ON dbo.Orders(custid, orderdate);
Following are the three queries you would use to handle these tasks, along with estimated subtree costs, as well as I/O, CPU and elapsed time statistics:
-- Query 1
-- Estimated Subtree Cost: 3.5344
-- logical reads: 2484, CPU time: 281 ms, elapsed time: 279 ms
SELECT shipperid, MAX(orderdate) AS maxod
FROM dbo.Orders
GROUP BY shipperid;
-- Query 2
-- Estimated Subtree Cost: 3.62798
-- logical reads: 2610, CPU time: 250 ms, elapsed time: 283 ms
SELECT empid, MAX(orderdate) AS maxod
FROM dbo.Orders
GROUP BY empid;
-- Query 3
-- Estimated Subtree Cost: 4.27624
-- logical reads: 3479, CPU time: 406 ms, elapsed time: 506 ms
SELECT custid, MAX(orderdate) AS maxod
FROM dbo.Orders
GROUP BY custid;
Figure 1 shows the plans for these queries:
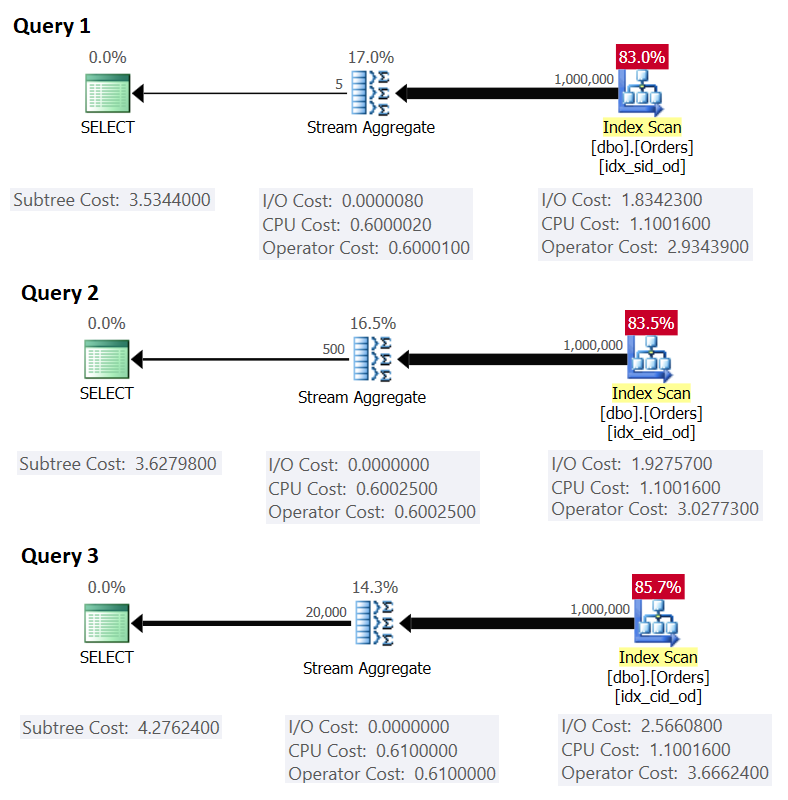 Figure 1: Plans for grouped queries
Figure 1: Plans for grouped queries
Recall that if you have a covering index in place, with the grouping set columns as the leading key columns, followed by the aggregation column, SQL Server is likely to choose a plan that performs an ordered scan of the covering index supporting the Stream Aggregate strategy. As is evident in the plans in Figure 1, the Index Scan operator is responsible for most of the plan cost, and within it the I/O part is the most prominent.
Before I present an alternative strategy and explain the circumstances under which it’s more optimal than the default strategy, let’s evaluate the cost of the existing strategy. Since the I/O part is the most dominant in determining the plan cost of this default strategy, let’s first just estimate how many logical page reads will be required. Later we’ll estimate the plan cost as well.
To estimate the number of logical reads that the Index Scan operator will require, you need to know how many rows you have in the table, and how many rows fit in a page based on the row size. Once you have these two operands, your formula for the required number of pages in the leaf level of the index is then CEILING(1e0 * @numrows / @rowsperpage). If all you have is just the table structure and no existing sample data to work with, you can use this article to estimate the number of pages you would have in the leaf level of the supporting index. If you have good representative sample data, even if not in the same scale as in the production environment, you can compute the average number of rows that fit in a page by querying catalog and dynamic management objects, like so:
SELECT I.name, row_count, in_row_data_page_count,
CAST(ROUND(1e0 * row_count / in_row_data_page_count, 0) AS INT) AS avgrowsperpage
FROM sys.indexes AS I
INNER JOIN sys.dm_db_partition_stats AS P
ON I.object_id = P.object_id
AND I.index_id = P.index_id
WHERE I.object_id = OBJECT_ID('dbo.Orders')
AND I.name IN ('idx_sid_od', 'idx_eid_od', 'idx_cid_od');
This query generates the following output in our sample database:
name row_count in_row_data_page_count avgrowsperpage ----------- ---------- ---------------------- --------------- idx_sid_od 1000000 2473 404 idx_eid_od 1000000 2599 385 idx_cid_od 1000000 3461 289
Now that you have the number of rows that fit in a leaf page of the index, you can estimate the total number of leaf pages in the index based on the number of rows you expect your production table to have. This will also be the expected number of logical reads to be applied by the Index Scan operator. In practice, there’s more to the number of reads that could take place than just the number of pages in the leaf level of the index, such as extra reads produced by the read ahead mechanism, but I’ll ignore those to keep our discussion simple.
For example, the estimated number of logical reads for Query 1 with respect to the expected number of rows is CEILING(1e0 * @numorws / 404). With 1,000,000 rows the expected number of logical reads is 2476. The difference between 2476 and the reported in row page count of 2473 can be attributed to the rounding I did when computing the average number of rows per page.
As for the plan cost, I explained how to reverse engineer the Stream Aggregate operator’s cost in Part 1 in the series. In a similar fashion, you can reverse engineer the cost of the Index Scan operator. The plan cost is then the sum of the costs of the Index Scan and Stream Aggregate operators.
To compute the cost of the Index Scan operator, you want to start with reverse engineering some of the important cost model constants:
@randomio = 0.003125 -- Random I/O cost @seqio = 0.000740740740741 -- Sequential I/O cost @cpubase = 0.000157 -- CPU base cost @cpurow = 0.0000011 -- CPU cost per row
With the above cost model constants figured out, you can proceed to reverse engineer the formulas for the I/O cost, CPU cost, and total operator cost for the Index Scan operator:
I/O cost: @randomio + (@numpages - 1e0) * @seqio = 0.003125 + (@numpages - 1e0) * 0.000740740740741 CPU cost: @cpubase + @numrows * @cpurow = 0.000157 + @numrows * 0.0000011 Operator cost: 0.002541259259259 + @numpages * 0.000740740740741 + @numrows * 0.0000011
For example, the Index Scan operator cost for Query 1, with 2473 pages and 1,000,000 rows, is:
0.002541259259259 + 2473 * 0.000740740740741 + 1000000 * 0.0000011 = 2.93439
Following is the reverse engineered formula for the Stream Aggregate operator cost:
0.000008 + @numrows * 0.0000006 + @numgroups * 0.0000005
As an example, for Query 1, we have 1,000,000 rows and 5 groups, hence the estimated cost is 0.6000105.
Combining the costs of the two operators, here’s the formula for the entire plan cost:
0.002549259259259 + @numpages * 0.000740740740741 + @numrows * 0.0000017 + @numgroups * 0.0000005
For Query 1, with 2473 pages, 1,000,000 rows, and 5 groups, you get:
0.002549259259259 + 2473 * 0.000740740740741 + 1000000 * 0.0000017 + 5 * 0.0000005 = 3.5344
This matches what Figure 1 shows as the estimated cost for Query 1.
If you relied on an estimated number of rows per page, your formula would be:
0.002549259259259 + CEILING(1e0 * @numrows / @rowsperpage) * 0.000740740740741 + @numrows * 0.0000017 + @numgroups * 0.0000005
As an example, for Query 1, with 1,000,000 rows, 404 rows per page, and 5 groups, the estimated cost is:
0.002549259259259 + CEILING(1e0 * 1000000 / 404) * 0.000740740740741 + 1000000 * 0.0000017 + 5 * 0.0000005 = 3.5366
As an exercise, you can apply the numbers for Query 2 (1,000,000 rows, 385 rows per page, 500 groups) and Query 3 (1,000,000 rows, 289 rows per page, 20,000 groups) in our formula, and see that the results match what Figure 1 shows.
Query tuning with query rewrites
The default preordered Stream Aggregate strategy for computing a MIN/MAX aggregate per group relies on an ordered scan of a supporting covering index (or some other preliminary activity that emits the rows ordered). An alternative strategy, with a supporting covering index present, would be to perform an index seek per group. Here’s a description of a pseudo plan based on such a strategy for a query that groups by grpcol and applies a MAX(aggcol):
set @curgrpcol = grpcol from first row obtained by a scan of the index, ordered forward;
while end of index not reached
begin
set @curagg = aggcol from row obtained by a seek to the last point
where grpcol = @curgrpcol, ordered backward;
emit row (@curgrpcol, @curagg);
set @curgrpcol = grpcol from row to the right of last row for current group;
end;
If you think about it, the default scan-based strategy is optimal when the grouping set has low density (large number of groups, with a small number of rows per group in average). The seeks-based strategy is optimal when the grouping set has high density (small number of groups, with a large number of rows per group in average). Figure 2 illustrates both strategies showing when each is optimal.
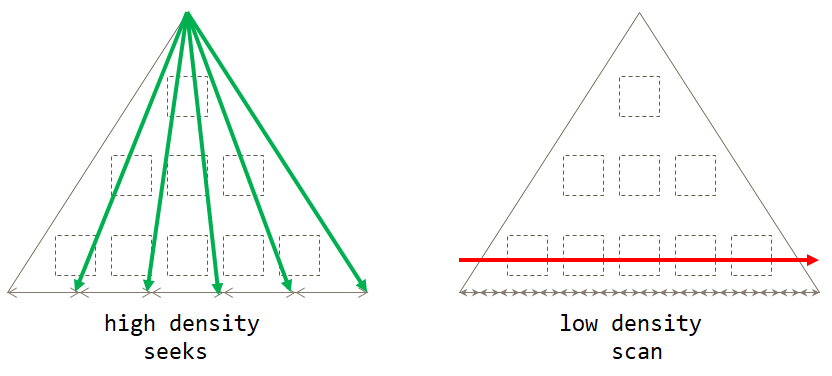 Figure 2: Optimal strategy based on grouping set density
Figure 2: Optimal strategy based on grouping set density
As long as you write the solution in the form of a grouped query, currently SQL Server will only consider the scan strategy. This will work well for you when the grouping set has low density. When you have high density, in order to get the seeks strategy, you will need to apply a query rewrite. One way to achieve this is to query the table that holds the groups, and to use a scalar aggregate subquery against the main table to obtain the aggregate. For instance, to compute the maximum order date for each shipper, you would use the following code:
SELECT shipperid,
( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.shipperid = S.shipperid
ORDER BY O.orderdate DESC ) AS maxod
FROM dbo.Shippers AS S;
The indexing guidelines for the main table are the same as the ones to support the default strategy. We already have those indexes in place for the three aforementioned tasks. You would probably also want a supporting index on the grouping set’s columns in the table holding the groups to minimize the I/O cost against that table. Use the following code to create such supporting indexes for our three tasks:
CREATE INDEX idx_sid ON dbo.Shippers(shipperid);
CREATE INDEX idx_eid ON dbo.Employees(empid);
CREATE INDEX idx_cid ON dbo.Customers(custid);
One small problem though is that the solution based on the subquery is not an exact logical-equivalent of the solution based on the grouped query. If you have a group with no presence in the main table, the former will return the group with a NULL as the aggregate, whereas the latter will not return the group at all. A simple way to achieve a true logical equivalent to the grouped query is to invoke the subquery using the CROSS APPLY operator in the FROM clause instead of using a scalar subquery in the SELECT clause. Remember that CROSS APPLY will not return a left row if the applied query returns an empty set. Here are the three solution queries implementing this strategy for our three tasks, along with their performance statistics:
-- Query 4
-- Estimated Subtree Cost: 0.0072299
-- logical reads: 2 + 15, CPU time: 0 ms, elapsed time: 43 ms
SELECT S.shipperid, A.orderdate AS maxod
FROM dbo.Shippers AS S
CROSS APPLY ( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.shipperid = S.shipperid
ORDER BY O.orderdate DESC ) AS A;
-- Query 5
-- Estimated Subtree Cost: 0.089694
-- logical reads: 2 + 1620, CPU time: 0 ms, elapsed time: 148 ms
SELECT E.empid, A.orderdate AS maxod
FROM dbo.Employees AS E
CROSS APPLY ( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.empid = E.empid
ORDER BY O.orderdate DESC ) AS A;
-- Query 6
-- Estimated Subtree Cost: 3.5227
-- logical reads: 45 + 63777, CPU time: 171 ms, elapsed time: 306 ms
SELECT C.custid, A.orderdate AS maxod
FROM dbo.Customers AS C
CROSS APPLY ( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.custid = C.custid
ORDER BY O.orderdate DESC ) AS A;
The plans for these queries are shown in Figure 3.
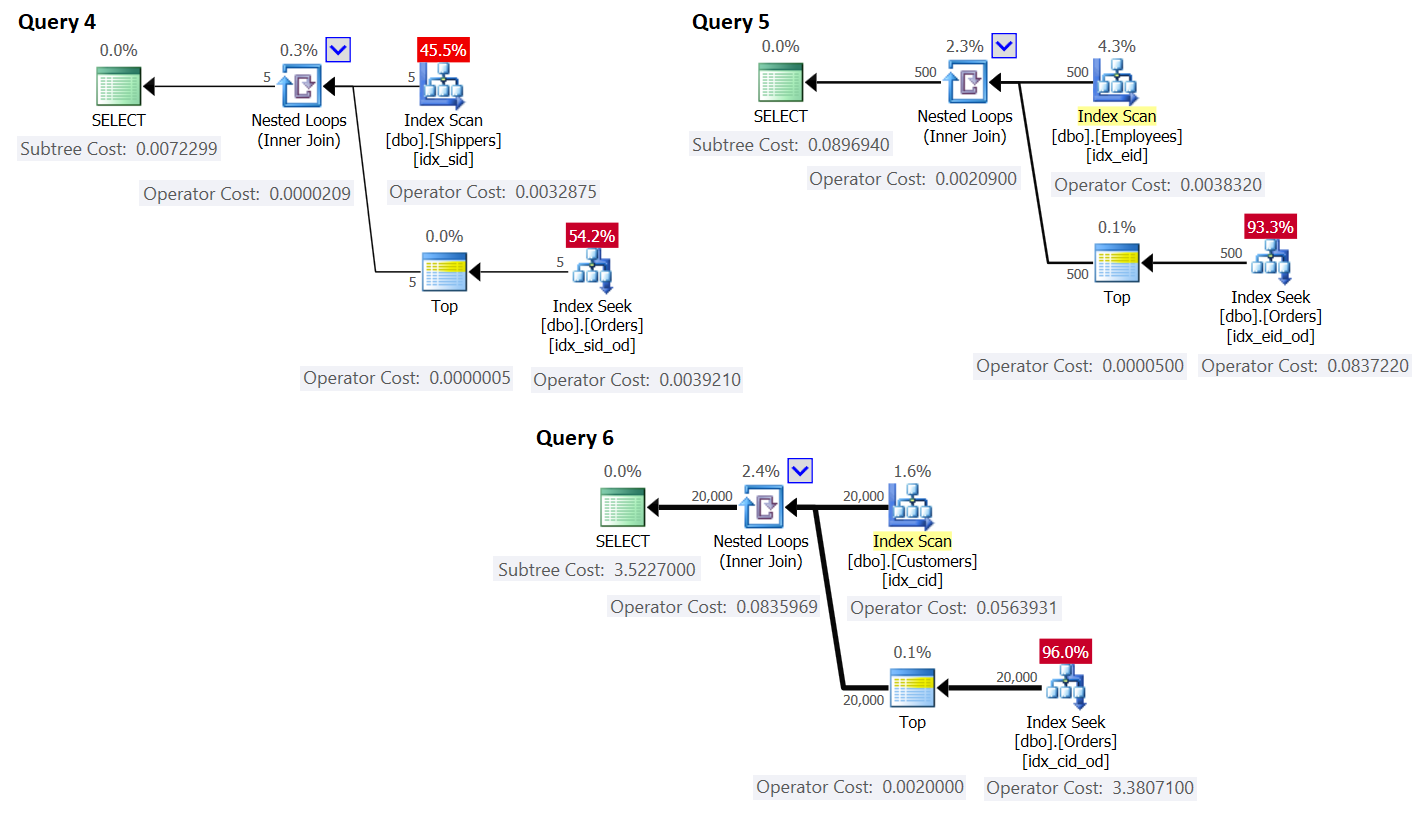 Figure 3: Plans for queries with rewrite
Figure 3: Plans for queries with rewrite
As you can see, the groups are obtained by scanning the index on the groups table, and the aggregate is obtained by applying a seek in the index on the main table. The higher the density of the grouping set, the more optimal this plan is compared to the default strategy for the grouped query.
Just like we did earlier for the default scan strategy, let’s estimate the number of logical reads and plan cost for the seeks strategy. The estimated number of logical reads is the number of reads for the single execution of the Index Scan operator that retrieves the groups, plus the reads for all of the executions of the Index Seek operator.
The estimated number of logical reads for the Index Scan operator is negligible compared to the seeks; still, it’s CEILING(1e0 * @numgroups / @rowsperpage). Take Query 4 as an example; say the index idx_sid fits about 600 rows per leaf page (actual number depends on actual shipperid values since the datatype is VARCHAR(5)). With 5 groups, all rows fit in a single leaf page. If you had 5,000 groups, they would fit in 9 pages.
The estimated number of logical reads for all executions of the Index Seek operator is @numgroups * @indexdepth. The depth of the index can be computed as:
CEILING(LOG(CEILING(1e0 * @numrows / @rowsperleafpage), @rowspernonleafpage)) + 1
Using Query 4 as an example, say that we can fit about 404 rows per leaf page of the index idx_sid_od, and about 352 rows per nonleaf page. Again, the actual numbers will depend on actual values stored in the shipperid column since its datatype is VARCHAR(5)). For estimates, remember that you can use the calculations described here. With good representative sample data available, you can use the following query to figure out the number of rows that can fit in the leaf and nonleaf pages of the given index:
SELECT
CASE P.index_level WHEN 0 THEN 'leaf' WHEN 1 THEN 'nonleaf' END AS pagetype,
FLOOR(8096 / (P.avg_record_size_in_bytes + 2)) AS rowsperpage
FROM (SELECT *
FROM sys.indexes
WHERE object_id = OBJECT_ID('dbo.Orders')
AND name = 'idx_sid_od') AS I
CROSS APPLY sys.dm_db_index_physical_stats
(DB_ID('PerformanceV3'), I.object_id, I.index_id, NULL, 'DETAILED') AS P
WHERE P.index_level <= 1;
I got the following output:
pagetype rowsperpage -------- ---------------------- leaf 404 nonleaf 352
With these numbers, the depth of the index with respect to the number of rows in the table is:
CEILING(LOG(CEILING(1e0 * @numrows / 404), 352)) + 1
With 1,000,000 rows in the table, this results in an index depth of 3. At about 50 million rows, the index depth increases to 4 levels, and at about 17.62 billion rows it increases to 5 levels.
At any rate, with respect to the number of groups and number of rows, assuming the above numbers of rows per page, the following formula computes the estimated number of logical reads for Query 4:
CEILING(1e0 * @numgroups / 600) + @numgroups * (CEILING(LOG(CEILING(1e0 * @numrows / 404), 352)) + 1)
For example, with 5 groups and 1,000,000 rows, you get only 16 reads total! Recall that the default scan-based strategy for the grouped query involves as many logical reads as CEILING(1e0 * @numrows / @rowsperpage). Using Query 1 as an example, and assuming about 404 rows per leaf page of the index idx_sid_od, with the same number of rows of 1,000,000, you get about 2,476 reads. Increase the number of rows in the table by a factor of 1,000 to 1,000,000,000, but keep the number of groups fixed. The number of reads required with the seeks strategy changes very little to 21, whereas the number of reads required with the scan strategy increases linearly to 2,475,248.
The beauty of the seeks strategy is that as long as the number of groups is small and fixed, it has almost constant scaling with respect to the number of rows in the table. That’s because the number of seeks is determined by the number of groups, and the depth of the index relates to the number of rows in the table in a logarithmic fashion where the log base is the number of rows that fit in a nonleaf page. Conversely, the scan-based strategy has linear scaling with respect to the number of rows involved.
Figure 4 shows the number of reads estimated for the two strategies, applied by Query 1 and Query 4, given a fixed number of groups of 5, and different numbers of rows in the main table.
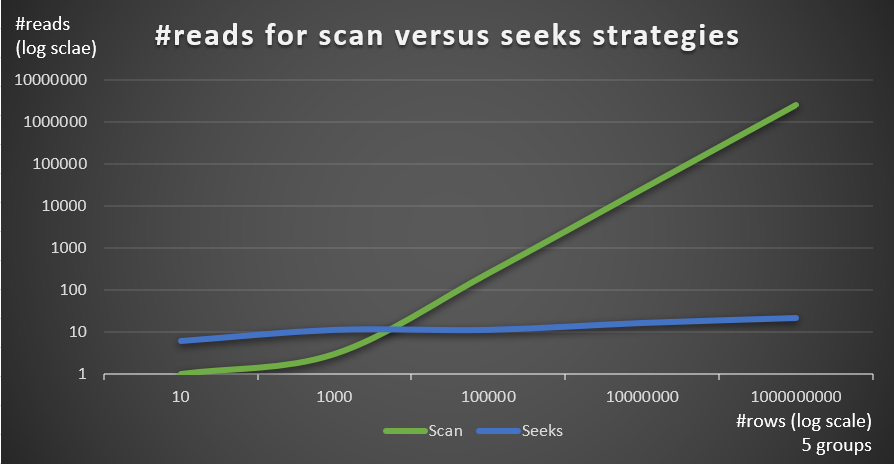 Figure 4: #reads for scan versus seeks strategies (5 groups)
Figure 4: #reads for scan versus seeks strategies (5 groups)
Figure 5 shows the number of reads estimated for the two strategies, given a fixed number of rows of 1,000,000 in the main table, and different numbers of groups.
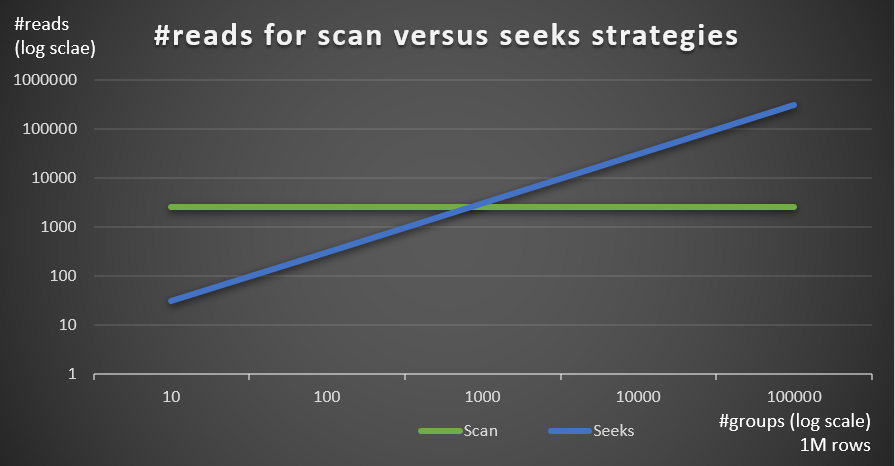 Figure 5: #reads for scan versus seeks strategies (1M rows)
Figure 5: #reads for scan versus seeks strategies (1M rows)
You can very clearly see that the higher the density of the grouping set (smaller number of groups) and the larger the main table, the more the seeks strategy is preferred in terms of the number of reads. If you’re wondering about the I/O pattern used by each strategy; sure, index seek operations perform random I/O, whereas an index scan operation performs sequential I/O. Still, it’s pretty clear which strategy is more optimal in the more extreme cases.
As for the query plan cost, again, using the plan for Query 4 in Figure 3 as an example, let’s break it down to the individual operators in the plan.
The reverse engineered formula for the cost of the Index Scan operator is:
0.002541259259259 + @numpages * 0.000740740740741 + @numgroups * 0.0000011
In our case, with 5 groups, all of which fit in one page, the cost is:
0.002541259259259 + 1 * 0.000740740740741 + 5 * 0.0000011 = 0.0032875
The cost shown in the plan is the same.
Like before, you could estimate the number of pages in the leaf level of the index based on the estimated number of rows per page using the formula CEILING(1e0 * @numrows / @rowsperpage), which in our case is CEILING(1e0 * @numgroups / @groupsperpage). Say the index idx_sid fits about 600 rows per leaf page, with 5 groups you would need to read one page. At any rate, the costing formula for the Index Scan operator then becomes:
0.002541259259259 + CEILING(1e0 * @numgroups / @groupsperpage) * 0.000740740740741 + @numgroups * 0.0000011
The reverse engineered costing formula for the Nested Loops operator is:
@executions * 0.00000418
In our case, this translates to:
@numgroups * 0.00000418
For Query 4, with 5 groups, you get:
5 * 0.00000418 = 0.0000209
The cost shown in the plan is the same.
The reverse engineered costing formula for the Top operator is:
@executions * @toprows * 0.00000001
In our case, this translates to:
@numgroups * 1 * 0.00000001
With 5 groups, you get:
5 * 0.0000001 = 0.0000005
The cost shown in the plan is the same.
As for the Index Seek operator, here I got great help from Paul White; thanks, my friend! The calculation is different for the first execution and for the rebinds (nonfirst executions that don’t reuse the previous execution’s result). Like we did with the Index Scan operator, let’s start with identifying the cost model’s constants:
@randomio = 0.003125 -- Random I/O cost @seqio = 0.000740740740741 -- Sequential I/O cost @cpubase = 0.000157 -- CPU base cost @cpurow = 0.0000011 -- CPU cost per row
For one execution, without a row goal applied, the I/O and CPU costs are:
I/O cost: @randomio + (@numpages - 1e0) * @seqio = 0.002384259259259 + @numpages * 0.000740740740741 CPU cost: @cpubase + @numrows * @cpurow = 0.000157 + @numrows * 0.0000011
Since we use TOP (1) we have only one page and one row involved, so the costs are:
I/O cost: 0.002384259259259 + 1 * 0.000740740740741 = 0.003125 CPU cost: 0.000157 + 1 * 0.0000011 = 0.0001581
So the cost of the first execution of the Index Seek operator in our case is:
@firstexecution = 0.003125 + 0.0001581 = 0.0032831
As for the cost of the rebinds, as usual, it’s made of CPU and I/O costs. Let’s call them @rebindcpu and @rebindio, respectively. With Query 4, having 5 groups, we have 4 rebinds (call it @rebinds). The @rebindcpu cost is the easy part. The formula is:
@rebindcpu = @rebinds * (@cpubase + @cpurow)
In our case, this translates to:
@rebindcpu = 4 * (0.000157 + 0.0000011) = 0.0006324
The @rebindio part is slightly more complex. Here, the costing formula computes, statistically, the expected number of distinct pages that the rebinds are expected to read using sampling with replacement. We’ll call this element @pswr (for distinct pages sampled with replacement). The idea is, we have @indexdatapages number of pages in the index (in our case, 2,473), and @rebinds number of rebinds (in our case, 4). Assuming we have the same probability to read any given page with each rebind, how many distinct pages are we expected to read in total? This is akin to having a bag with 2,473 balls, and four times blindly drawing a ball from the bag and then returning it to the bag. Statistically, how many distinct balls are you expected to draw in total? The formula for this, using our operands, is:
@pswr = @indexdatapages * (1e0 - POWER((@indexdatapages - 1e0) / @indexdatapages, @rebinds))
With our numbers you get:
@pswr = 2473 * (1e0 - POWER((2473 - 1e0) / 2473, 4)) = 3.99757445099277
Next, you compute the number of rows and pages you have in average per group:
@grouprows = @cardinality * @density @grouppages = CEILING(@indexdatapages * @density)
In our Query 4, the cardinality is 1,000,000 and the density is 1/5 = 0.2. So you get:
@grouprows = 1000000 * 0.2 = 200000 @numpages = CEILING(2473 * 0.2) = 495
Then you compute the I/O cost without filtering (call it @io) as:
@io = @randomio + (@seqio * (@grouppages - 1e0))
In our case, you get:
@io = 0.003125 + (0.000740740740741 * (495 - 1e0)) = 0.369050925926054
And lastly, since the seek extracts only one row in each rebind, you compute @rebindio using the following formula:
@rebindio = (1e0 / @grouprows) * ((@pswr - 1e0) * @io)
In our case, you get:
@rebindio = (1e0 / 200000) * ((3.99757445099277 - 1e0) * 0.369050925926054) = 0.000005531288
Finally, the operator’s cost is:
Operator cost: @firstexecution + @rebindcpu + @rebindio = 0.0032831 + 0.0006324 + 0.000005531288 = 0.003921031288
This is the same as the Index Seek operator cost shown in the plan for Query 4.
You can now aggregate the costs of all of the operators to get the complete query plan cost. You get:
Query plan cost: 0.002541259259259 + CEILING(1e0 * @numgroups / @groupsperpage)
* 0.000740740740741 + @numgroups * 0.0000011
+ @numgroups * 0.00000418
+ @numgroups * 0.00000001
+ 0.0032831 + (@numgroups - 1e0) * 0.0001581
+ (1e0 / (@numrows / @numgroups)) * (CEILING(1e0 * @numrows / @rowsperpage)
* (1e0 - POWER((CEILING(1e0 * @numrows / @rowsperpage) - 1e0)
/ CEILING(1e0 * @numrows / @rowsperpage), @numgroups - 1e0)) - 1e0)
* (0.003125 + (0.000740740740741 * (CEILING((@numrows / @rowsperpage)
* (1e0 / @numgroups)) - 1e0)))
After simplification, you get the following complete costing formula for our Seeks strategy:
0.005666259259259 + CEILING(1e0 * @numgroups / @groupsperpage)
* 0.000740740740741 + @numgroups * 0.0000011
+ @numgroups * 0.00016229
+ (1e0 / (@numrows / @numgroups)) * (CEILING(1e0 * @numrows / @rowsperpage)
* (1e0 - POWER((CEILING(1e0 * @numrows / @rowsperpage) - 1e0)
/ CEILING(1e0 * @numrows / @rowsperpage), @numgroups - 1e0)) - 1e0)
* (0.003125 + (0.000740740740741 * (CEILING((@numrows / @rowsperpage)
* (1e0 / @numgroups)) - 1e0)))
As an example, using T-SQL, here’s the computation of the query plan cost with our Seeks strategy for Query 4:
DECLARE
@numrows AS FLOAT = 1000000,
@numgroups AS FLOAT = 5,
@rowsperpage AS FLOAT = 404,
@groupsperpage AS FLOAT = 600;
SELECT
0.005666259259259 + CEILING(1e0 * @numgroups / @groupsperpage)
* 0.000740740740741 + @numgroups * 0.0000011
+ @numgroups * 0.00016229
+ (1e0 / (@numrows / @numgroups)) * (CEILING(1e0 * @numrows / @rowsperpage)
* (1e0 - POWER((CEILING(1e0 * @numrows / @rowsperpage) - 1e0)
/ CEILING(1e0 * @numrows / @rowsperpage), @numgroups - 1e0)) - 1e0)
* (0.003125 + (0.000740740740741 * (CEILING((@numrows / @rowsperpage)
* (1e0 / @numgroups)) - 1e0)))
AS seeksplancost;
This calculation computes the cost 0.0072295 for Query 4. The estimated cost shown in Figure 3 is 0.0072299. That’s pretty close! As an exercise, compute the costs for Query 5 and Query 6 using this formula and verify that you get numbers close to the ones shown in Figure 3.
Recall that the costing formula for the default scan-based strategy is (call it Scan strategy):
0.002549259259259 + CEILING(1e0 * @numrows / @rowsperpage) * 0.000740740740741 + @numrows * 0.0000017 + @numgroups * 0.0000005
Using Query 1 as an example, and assuming 1,000,000 rows in the table, 404 rows per page, and 5 groups, the estimated query plan cost of the scan strategy is 3.5366.
Figure 6 shows the estimated query plan costs for the two strategies, applied by Query 1 (scan) and Query 4 (seeks), given a fixed number of groups of 5, and different numbers of rows in the main table.
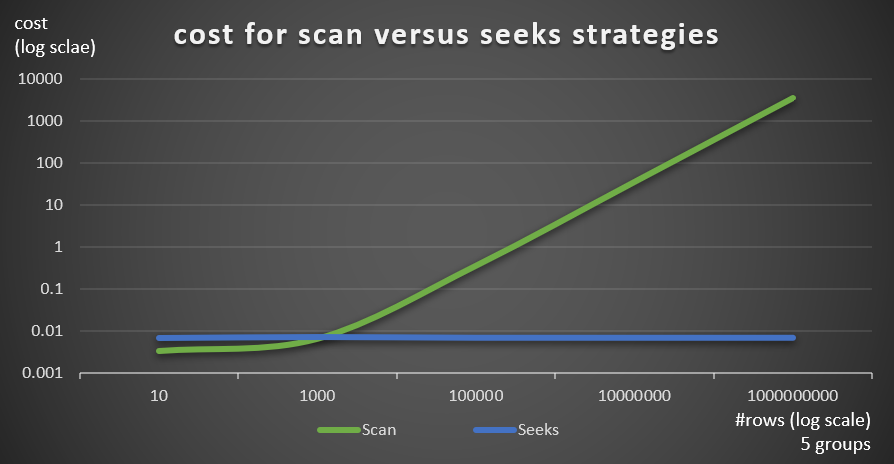 Figure 6: cost for scan versus seeks strategies (5 groups)
Figure 6: cost for scan versus seeks strategies (5 groups)
Figure 7 shows the estimated query plan costs for the two strategies, given a fixed number of rows in the main table of 1,000,000, and different numbers of groups.
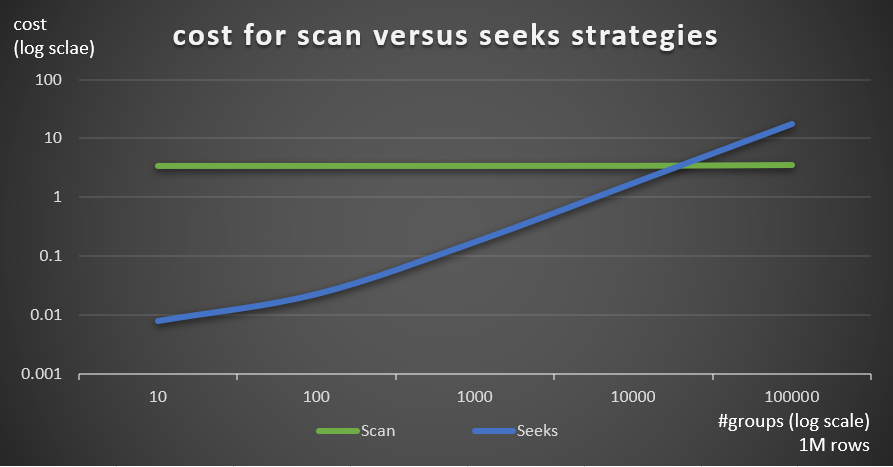 Figure 7: cost for scan versus seeks strategies (1M rows)
Figure 7: cost for scan versus seeks strategies (1M rows)
As is evident from these findings, the higher the grouping set density and the more rows in the main table, the more optimal the seeks strategy is compared to the scan strategy. So, in high density scenarios, make sure you try the APPLY-based solution. In the meanwhile, we can hope that Microsoft will add this strategy as a built-in option for grouped queries.
Conclusion
This article concludes a five-part series on query optimization thresholds for queries that group and aggregate data. One goal of the series was to discuss the specifics of the various algorithms that the optimizer can use, the conditions under which each algorithm is preferred, and when you should intervene with your own query rewrites. Another goal was to explain the process of discovering the various options and comparing them. Obviously, the same analysis process can be applied to filtering, joining, windowing, and many other aspects of query optimization. Hopefully, you now feel more equipped to deal with query tuning than before.







The cost model formulas go back to SQL Server 7.0 (not sure if earlier)
see http://www.qdpma.com/CBO/s2kCBO.html
there were some changes and corrections in version 2005, which is largely what is in place (sorry, but I stopped checking around 2014)
http://www.qdpma.com/CBO/CBO02_IndexSeek.html
Hey Joe!
I'd be surprised if the current cost model formulas go back prior to SQL Server 7.0 since that's the point that both the relational engine and storage engine went through major changes. Remember the 6.5 days when the page size was 2 KB, the optimizer could use only one index per table, and a heap was organized as a linked list? :)
Thanks for the links! Good to see that you cover some of the costing details.
Cheers,
Itzik