Recently I covered some of the T-SQL improvements in SQL Server 2022 here, and Aaron Bertrand covered additional improvements here. Those improvements were introduced in CTP 2.0.
Microsoft just announced the release of SQL Server 2022 CTP 2.1. This release includes a number of additional interesting T-SQL improvements, which include:
- The distinct predicate
- The approximate percentile functions APPROX_PERCENTILE_CONT and APPROX_PERCENTILE_DISC
- The DATETRUNC function
- A set of bit manipulation functions
In this article, I focus on the distinct predicate and the approximate percentile functions. I’ll cover the other improvements in future articles since there’s a lot to say about those.
I’ll be using the sample database TSQLV6 in the examples in this article. You can download this sample database here.
The Distinct Predicate
If you’ve been writing and optimizing T-SQL code for a while, you’re probably well aware of the many complexities involved with NULL handling. If you need a refresher, check out the following articles:
- NULL complexities – Part 1
- NULL complexities – Part 2
- NULL complexities – Part 3
- NULL complexities – Part 4
One of the complexities that is of a specific importance to this section is comparisons that potentially involve NULL comparands, such as ones that you use in filter and join predicates. Most operators that you use in such comparisons, including the equals (=) and different than (<>) operators, use three-valued logic. This means that there are three possible truth values as a result of a predicate that uses such operators: true, false and unknown. When both comparands are non-NULL, such operators return true or false as you would intuitively expect. When any of the comparands is NULL, including when both are NULL, such comparisons return the unknown truth value. Both filter and join predicates consider unknown as a non-match, and sometimes that’s not the behavior that you’re after.
To demonstrate the problem, consider the following example:
DECLARE @dt AS DATE = '20220212';
SELECT orderid, shippeddate
FROM Sales.Orders
WHERE shippeddate = @dt;
I’m using a local variable and an ad-hoc query here for simplicity, but imagine this was a stored procedure that accepts an input shipping date as a parameter called @dt and returns all orders that were shipped on the input date.
When passing a non-NULL shipping date as input, such as in this example, you indeed get the orders that were shipped on the input date, as expected:
orderid shippeddate ----------- ----------- 10865 2022-02-12 10866 2022-02-12 10876 2022-02-12 10878 2022-02-12 10879 2022-02-12
For orders with the same non-NULL shipping date as the input, the filter predicate evaluates to true, and such orders are returned. For orders with a non-NULL shipping date that is different from the input the filter predicate evaluates to false, and such orders are discarded. For orders with a NULL shipping date (unshipped orders), the filter predicate evaluates to unknown, and such orders are discarded as well. So far so good.
This filter predicate is considered a search argument, or SARG, in short. This means that SQL Server can potentially apply an index seek based on the predicate in a supporting index, if one exists, thus reading only index leaf pages with qualifying rows, as opposed to scanning all rows.
The plan for this query is shown in Figure 1, affirming that the query’s filter predicate is indeed used as a seek predicate.
Figure 1: Plan showing an index seek
But what if you want to filter only unshipped orders, and to achieve this you pass a NULL as input:
DECLARE @dt AS DATE = NULL;
SELECT orderid, shippeddate
FROM Sales.Orders
WHERE shippeddate = @dt;
Recall that when using the equals (=) operator, when any of the comparands is NULL, including when both are NULL, you get unknown as the result truth value, and a filter predicate discards the unknown cases. This query returns an empty set despite the fact there are a few unshipped orders with a NULL shipping date:
orderid shippeddate ----------- ----------- (0 rows affected)
A common workaround is to use the COALESCE or ISNULL functions in both sides of the predicate, so that when the inputs are NULL, they’re replaced with a non-NULL value that is normally not used in the data, like so:
DECLARE @dt AS DATE = NULL;
SELECT orderid, shippeddate
FROM Sales.Orders
WHERE ISNULL(shippeddate, '99991231') = ISNULL(@dt, '99991231');
This time you do correctly get the desired unshipped orders when you pass a NULL as input:
orderid shippeddate ----------- ----------- 11008 NULL 11019 NULL 11039 NULL 11040 NULL 11045 NULL 11051 NULL 11054 NULL 11058 NULL 11059 NULL 11061 NULL 11062 NULL 11065 NULL 11068 NULL 11070 NULL 11071 NULL 11072 NULL 11073 NULL 11074 NULL 11075 NULL 11076 NULL 11077 NULL
That problem is that the fact that you applied manipulation to the filtered column with the ISNULL function prevents the predicate from being a SARG, and you end up with a plan that scans all rows, as shown in Figure 2.
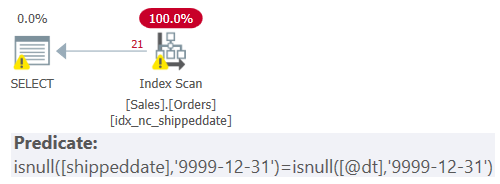Figure 2: Plan showing an index scan
Another workaround is to use a lengthier predicate that involves a combination of equals (=) and IS NULL operators, like so:
DECLARE @dt AS DATE = NULL;
SELECT orderid, shippeddate
FROM Sales.Orders
WHERE shippeddate = @dt OR (shippeddate IS NULL AND @dt IS NULL);
This predicate is considered a SARG and results in a plan with an index seek. However, it is a bit lengthy and awkward.
SQL Server 2022 introduces a standard feature called the distinct predicate, which is designed to apply comparisons using two-valued logic, treating NULLs like non-NULL values. The distinct predicate uses the following syntax:
The two-valued-logic counterpart to the equals (=) operator is the IS NOT DISTINCT FROM operator. Similarly, the two-valued-logic counterpart to the different than (<>) operator is the IS DISTINCT FROM operator.
So in order to get orders that were shipped on the input date when the input is non-NULL, and unshipped orders with a NULL shipped date when the input is NULL, use the IS NOT DISTINCT FROM operator, like so:
DECLARE @dt AS DATE = NULL;
SELECT orderid, shippeddate
FROM Sales.Orders
WHERE shippeddate IS NOT DISTINCT FROM @dt;
This specific execution does return all unshipped orders since the input is NULL. And the good news is that this predicate is considered a SARG, resulting in a plan with an index seek.
Suppose that you want to return orders shipped on a different date than the input, treating NULLs like non-NULLs. Without the distinct predicate you could mix the use of the different than (<>) , IS NULL and IS NOT NULL operators, like so:
DECLARE @dt AS DATE = NULL;
SELECT orderid, shippeddate
FROM Sales.Orders
WHERE shippeddate <> @dt
OR (shippeddate IS NULL AND @dt IS NOT NULL)
OR (shippeddate IS NOT NULL AND @dt IS NULL);
This specific execution returns shipped orders, generating the following output:
orderid shippeddate ----------- ----------- 10249 2020-07-10 10252 2020-07-11 10250 2020-07-12 10251 2020-07-15 10255 2020-07-15 ... 11050 2022-05-05 11055 2022-05-05 11063 2022-05-06 11067 2022-05-06 11069 2022-05-06 (809 rows affected)
Achieving the same with the distinct predicate is so much simpler:
DECLARE @dt AS DATE = NULL;
SELECT orderid, shippeddate
FROM Sales.Orders
WHERE shippeddate IS DISTINCT FROM @dt;
You can use the distinct predicate wherever you can use predicates in T-SQL. For example, suppose that prior to SQL Server 2022 you had the following query:
SELECT ...
FROM T1
INNER JOIN T2
ON T1.col1 = T2.col1 OR (T1.col1 IS NULL AND T2.col1 IS NULL)
AND T1.col2 = T2.col2 OR (T1.col2 IS NULL AND T2.col2 IS NULL)
AND T1.col3 = T2.col3 OR (T1.col3 IS NULL AND T2.col3 IS NULL);
The query joins the tables T1 and T2, matching the NULLable columns col1, col2 and col3 between the two sides.
Achieving the same using the distinct predicate in SQL Server 2022 is, again, so much simpler:
SELECT ...
FROM T1
INNER JOIN T2
ON T1.col1 IS NOT DISTINCT FROM T2.col1
AND T1.col2 IS NOT DISTINCT FROM T2.col2
AND T1.col3 IS NOT DISTINCT FROM T2.col3;
Just like a SARGable filter predicate using IS NOT DISTINCT FROM can support an index seek, such a join predicate can support a Merge join algorithm based on ordered index scans.
The Approximate Percentile Functions
If you needed to compute percentiles in the past, you’re probably aware that T-SQL already had support for such calculations using the functions PERCENTILE_CONT (an interpolated percentile based on a continuous distribution model) and PERCENTILE_DISC (an existing value based on a discrete distribution model). Both functions were, and at the time of writing still are, available only as window functions.
For example, the following query computes both the continuous and the discrete median (0.5 percentile) scores per test, returning those alongside each student test score details:
USE TSQLV6;
SELECT testid, studentid, score, testid,
PERCENTILE_CONT (0.5) WITHIN GROUP (ORDER BY score)
OVER (PARTITION BY testid) AS medianscore_cont,
PERCENTILE_DISC (0.5) WITHIN GROUP (ORDER BY score)
OVER (PARTITION BY testid) AS medianscore_disc
FROM Stats.Scores;
This code generates the following output:
testid studentid score testid medianscore_cont medianscore_disc ---------- ---------- ----- ---------- ---------------------- ---------------- Test ABC Student E 50 Test ABC 75 75 Test ABC Student C 55 Test ABC 75 75 Test ABC Student D 55 Test ABC 75 75 Test ABC Student H 65 Test ABC 75 75 Test ABC Student I 75 Test ABC 75 75 Test ABC Student B 80 Test ABC 75 75 Test ABC Student F 80 Test ABC 75 75 Test ABC Student A 95 Test ABC 75 75 Test ABC Student G 95 Test ABC 75 75 Test XYZ Student E 50 Test XYZ 77.5 75 Test XYZ Student C 55 Test XYZ 77.5 75 Test XYZ Student D 55 Test XYZ 77.5 75 Test XYZ Student H 65 Test XYZ 77.5 75 Test XYZ Student I 75 Test XYZ 77.5 75 Test XYZ Student B 80 Test XYZ 77.5 75 Test XYZ Student F 80 Test XYZ 77.5 75 Test XYZ Student A 95 Test XYZ 77.5 75 Test XYZ Student G 95 Test XYZ 77.5 75 Test XYZ Student J 95 Test XYZ 77.5 75
If you’re using T-SQL to compute percentiles as part of your work, these functions should be familiar to you since they’ve been supported in SQL Server 2005 and later.
The continuous median computation assumes a continuous distribution of the test scores, so if there’s no exact middle point, it interpolates the median from the score before and score after the nonexistent middle. For example, in the case of Test XYZ there are 10 test scores, with no actual middle score. The result median score 77.5 is interpolated as the mid score between the two existing middle scores 75 and 80. The discrete median calculation returns the closest existing score to the requested percentile, or the first of the two if they are of the same distance from the nonexistent one. That’s why it returns the score 75 for Test XYZ. For Test ABC there are 9 scores, so there’s an actual middle point—the fifth score 75, so both functions return the same value.
One obvious benefit of these functions is that they are accurate. Another is that if you need the windowed version of the calculations, that’s how they are implemented. The windowed version allows you to return the function’s result alongside detail elements from the table like in the above query. Perhaps you need to involve a detail element like the current score with the percentile value in the same expression, like computing the difference between the current and median scores.
But there are also downsides to the existing functions. Computing accurate percentiles has negative implications in terms of memory footprint and performance. Also, often you need to compute and return percentiles only once per group, and that’s not how window functions work. So, with the existing windowed version of the accurate percentile functions, you have to resort to computing them alongside the detail elements, and adding a DISTINCT clause to eliminate the duplicates, like so:
SELECT DISTINCT testid,
PERCENTILE_CONT (0.5) WITHIN GROUP (ORDER BY score)
OVER (PARTITION BY testid) AS medianscore_cont,
PERCENTILE_DISC (0.5) WITHIN GROUP (ORDER BY score)
OVER (PARTITION BY testid) AS medianscore_disc
FROM Stats.Scores;
This code generates the following output:
testid medianscore_cont medianscore_disc ---------- ---------------------- ---------------- Test ABC 75 75 Test XYZ 77.5 75
Computing windowed percentiles and then eliminating duplicates with DISTINCT is not the end of the world, but it is a bit awkward. Also, a grouped version of these functions would have lent itself to better optimization.
SQL Server 2022 introduces two approximate percentile functions called APPROX_PERCENTILE_CONT and APPROX_PERCENTILE_DISC. These functions have two main benefits compared to their older, accurate, counterparts. One benefit is that if you’re okay with a performance versus accuracy tradeoff, the new functions are faster and have a smaller memory footprint than the older ones. Another benefit is that these functions are implemented as grouped ordered set functions. Here’s an example for using them to get both the continuous and the discrete median test scores:
SELECT testid,
APPROX_PERCENTILE_CONT (0.5) WITHIN GROUP (ORDER BY score) AS medianscore_cont,
APPROX_PERCENTILE_DISC (0.5) WITHIN GROUP (ORDER BY score) AS medianscore_disc
FROM Stats.Scores
GROUP BY testid;
This code generates the following output:
testid medianscore_cont medianscore_disc ---------- ---------------------- ---------------- Test ABC 75 75 Test XYZ 77.5 75
I ran a similar query with the approximate functions against a table with 1,000,000 rows on a commodity machine, and got the following perf stats:
CPU time = 1077 ms, elapsed time = 344 ms. Memory grant 12 MB
Using the accurate window functions combined with a DISTINCT clause, I got the following perf stats:
CPU time = 12094 ms, elapsed time = 3356 ms. Memory grant 195 MB
As you can see, that’s a pretty dramatic difference.
For the new functions, Microsoft uses an implementation that approximates the percentiles from a stream using compressed data structures based on a method called KLL. According to the documentation, the error margin is 1.33% (based on ranks not values) within a 99% confidence. You should also be aware that the implementation uses randomization in how it picks the values, so running the query multiple times, you can get different results without the underlying data changing.
Unfortunately, at the time of writing, T-SQL neither supports a grouped version of the accurate percentile functions, nor a windowed version of the approximate percentile functions. This could be tricky if, for example, you start with a grouped query that uses an approximate percentile function, and at a later point realize that you need to convert it to guarantee an accurate calculation. Hopefully we’ll see support in T-SQL for the missing counterparts at some point in the future.
Conclusion
In this article I focused on a couple of the T-SQL improvements in SQL Server 2022, specially out of those that were added in CTP 2.1.
The standard distinct predicate compares elements using a distinctness concept instead of equality or inequality, simplifying comparisons involving NULLs. It’s great to see that it was implemented as a search argument (SARG), efficiently utilizing indexing.
The approximate percentile functions APPROX_PERCENTILE_CONT and APPROX_PERCENTLILE_DISC give you an option to compute percentiles as approximate ones efficiently. Compared to the previously available PERCENTILE_CONT and PERCENTILE_DISC functions, the new functions may be faster and require less memory, but they don’t guarantee accurate results. Also, the older functions are designed as window functions and currently not available as grouped functions. The new functions are designed as grouped functions. So when converting code that uses one version of the function to the other, you’ll need to apply some query rewriting. It would be good if in the future T-SQL supported both windowed and grouped versions of both the accurate and the approximate functions.
As mentioned, in future articles I’ll continue the coverage of the other T-SQL improvements in SQL Server 2022.
