Matching Supply With Demand — Solutions, Part 2

In this article, I continue the coverage of solutions to Peter Larsson’s enticing matching supply with demand challenge. Thanks again to Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie, and Peter Larsson, for sending your solutions.

Last month I covered a solution based on interval intersections, using a classic predicate-based interval intersection test. I’ll refer to that solution as classic intersections. The classic interval intersections approach results in a plan with quadratic scaling (N^2). I demonstrated its poor performance against sample inputs ranging from 100K to 400K rows. It took the solution 931 seconds to complete against the 400K-row input! This month I’ll start by briefly reminding you of last month’s solution and why it scales and performs so badly. I’ll then introduce an approach based on a revision to the interval intersection test. This approach was used by Luca, Kamil, and possibly also Daniel, and it enables a solution with much better performance and scaling. I’ll refer to that solution as revised intersections.

The Problem With the Classic Intersection Test

Let’s start with a quick reminder of last month’s solution.

I used the following indexes on the input dbo.Auctions table to support the computation of the running totals that produce the demand and supply intervals:

-- Index to support solution

CREATE UNIQUE NONCLUSTERED INDEX idx_Code_ID_i_Quantity
  ON dbo.Auctions(Code, ID)
  INCLUDE(Quantity);

-- Enable batch-mode Window Aggregate

CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs
  ON dbo.Auctions(ID)
  WHERE ID = -1 AND ID = -2;

The following code has the complete solution implementing the classic interval intersections approach:

-- Drop temp tables if exist

SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO

WITH D0 AS

-- D0 computes running demand as EndDemand

(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),

-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval

D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID,
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;

WITH S0 AS

-- S0 computes running supply as EndSupply

(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),

-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval

S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;

CREATE UNIQUE CLUSTERED INDEX idx_cl_ES_ID ON #Supply(EndSupply, ID);

-- Trades are the overlapping segments of the intersecting intervals

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S WITH (FORCESEEK)
    ON D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply;

This code starts by computing the demand and supply intervals and writing those to temporary tables called #Demand and #Supply. The code then creates a clustered index on #Supply with EndSupply as the leading key to support the intersection test as best as possible. Finally, the code joins #Supply and #Demand, identifying trades as the overlapping segments of the intersecting intervals, using the following join predicate based on the classic interval intersection test:

D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply

The plan for this solution is shown in Figure 1.

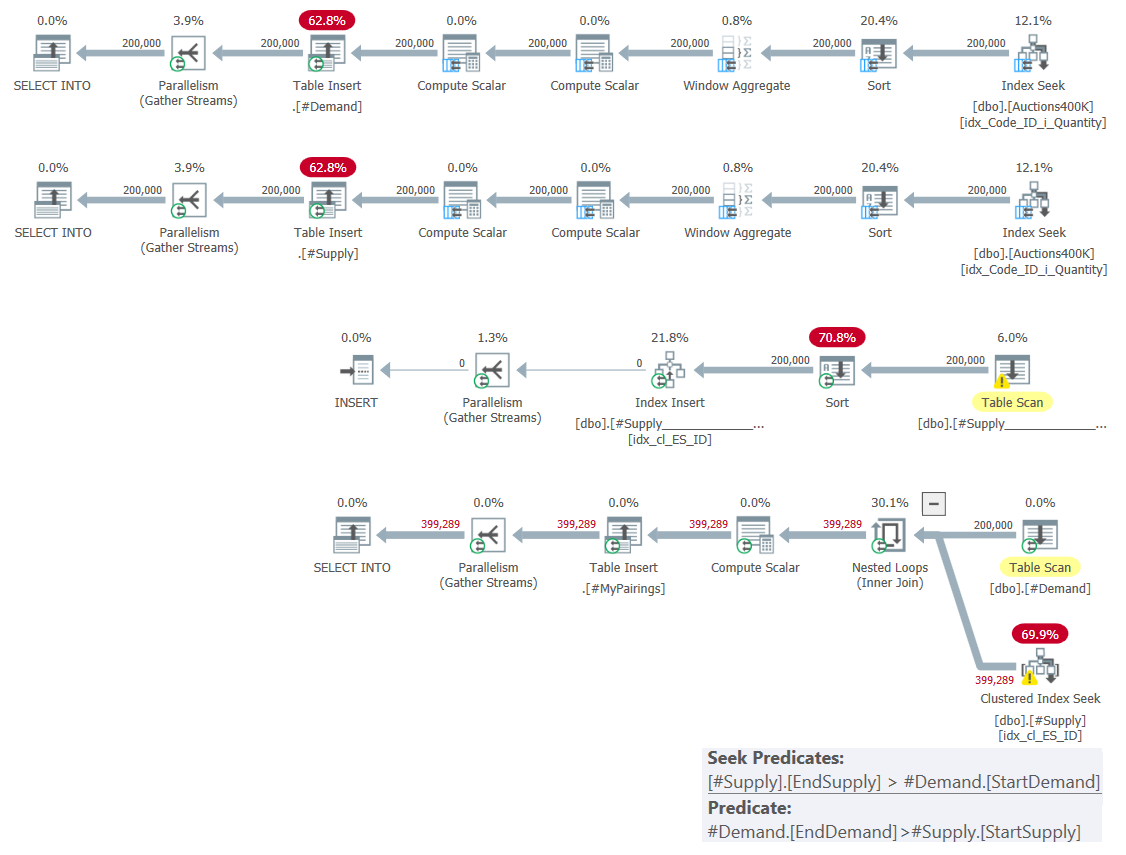Figure 1: Query plan for solution based on classic intersections

As I explained last month, among the two range predicates involved, only one can be used as a seek predicate as part of an index seek operation, whereas the other has to be applied as a residual predicate. You can clearly see this in the plan for the last query in Figure 1. That’s why I only bothered creating one index on one of the tables. I also forced the use of a seek in the index I created using the FORCESEEK hint. Otherwise, the optimizer could end up ignoring that index and creating one of its own using an Index Spool operator.

This plan has quadratic complexity since per row in one side—#Demand in our case—the index seek will have to access in average half the rows in the other side—#Supply in our case—based on the seek predicate, and identify the final matches by applying the residual predicate.

If it’s still unclear to you why this plan has quadratic complexity, perhaps a visual depiction of the work could help, as shown in Figure 2.

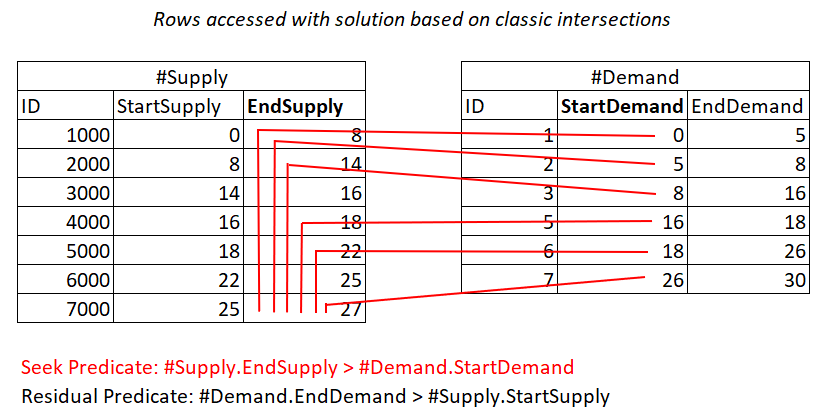Figure 2: Illustration of work with solution based on classic intersections

This illustration represents the work done by the Nested Loops join in the plan for the last query. The #Demand heap is the outer input of the join and the clustered index on #Supply (with EndSupply as the leading key) is the inner input. The red lines represent the index seek activities done per row in #Demand in the index on #Supply and the rows they access as part of the range scans in the index leaf. Towards extreme low StartDemand values in #Demand, the range scan needs to access close to all rows in #Supply. Towards extreme high StartDemand values in #Demand, the range scan needs to access close to zero rows in #Supply. On average, the range scan needs to access about half the rows in #Supply per row in demand. With D demand rows and S supply rows, the number of rows accessed is D + D*S/2. That’s in addition to the cost of the seeks that get you to the matching rows. For example, when filling dbo.Auctions with 200,000 demand rows and 200,000 supply rows, this translates to the Nested Loops join accessing 200,000 demand rows + 200,000*200,000/2 supply rows, or 200,000 + 200,000^2/2 = 20,000,200,000 rows accessed. There’s a lot of rescanning of supply rows happening here!

If you want to stick to the interval intersections idea but get good performance, you need to come up with a way to reduce the amount of work done.

In his solution, Joe Obbish bucketized the intervals based on the maximum interval length. This way he was able to reduce the number of rows the joins needed to handle and rely on batch processing. He used the classic interval intersection test as a final filter. Joe’s solution works well as long as the maximum interval length is not very high, but the solution’s runtime increases as the maximum interval length increases.

So, what else can you do…?

Revised Intersection Test

Luca, Kamil, and possibly Daniel (there was an unclear part about his posted solution due to the website’s formatting, so I had to guess) used a revised interval intersection test that enables much better utilization of indexing.

Their intersection test is a disjunction of two predicates (predicates separated by OR operator):

   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >= D.StartDemand AND S.StartSupply < D.EndDemand)

In English, either the demand start delimiter intersects with the supply interval in an inclusive, exclusive manner (including the start and excluding the end); or the supply start delimiter intersects with the demand interval, in an inclusive, exclusive manner. To make the two predicates disjoint (not have overlapping cases) yet still complete in covering all cases, you can keep the = operator in just one or the other, for example:

   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand)

This revised interval intersection test is quite insightful. Each of the predicates can potentially efficiently use an index. Consider predicate 1:

D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
^^^^^^^^^^^^^                      ^^^^^^^^^^^^^

Assuming you create a covering index on #Demand with StartDemand as the leading key, you can potentially get a Nested Loops join applying the work illustrated in Figure 3.

Figure 3: Illustration of theoretical work required to process predicate 1

Yes, you still pay for a seek in the #Demand index per row in #Supply, but the range scans in the index leaf access almost disjoint subsets of rows. No rescanning of rows!

The situation is similar with predicate 2:

S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand
^^^^^^^^^^^^^                     ^^^^^^^^^^^^^

Assuming you create a covering index on #Supply with StartSupply as the leading key, you can potentially get a Nested Loops join applying the work illustrated in Figure 4.

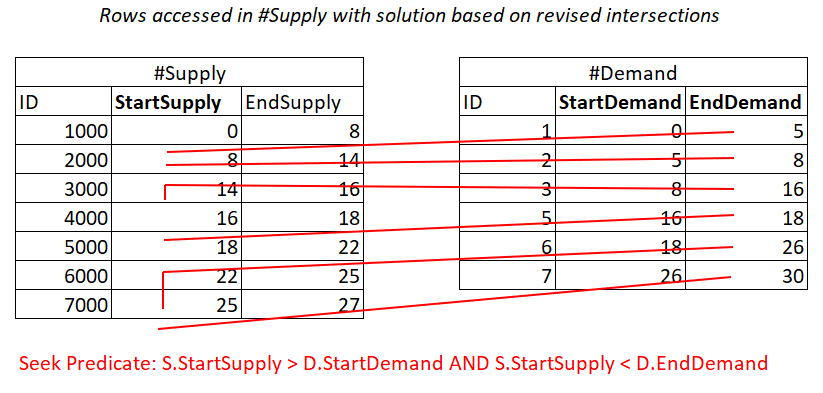
Figure 4: Illustration of theoretical work required to process predicate 2

Also, here you pay for a seek in the #Supply index per row in #Demand, and then the range scans in the index leaf access almost disjoint subsets of rows. Again, no rescanning of rows!

Assuming D demand rows and S supply rows, the work can be described as:

Number of index seek operations: D  + S
Number of rows accessed:         2D + 2S

So likely, the biggest portion of the cost here is the I/O cost involved with the seeks. But this part of the work has linear scaling compared to the quadratic scaling of the classic interval intersections query.

Of course, you need to consider the preliminary cost of the index creation on the temporary tables, which has n log n scaling due to the sorting involved, but you pay this part as a preliminary part of both solutions.

Let’s try and put this theory into practice. Let’s start by populating the #Demand and #supply temporary tables with the demand and supply intervals (same as with the classic interval intersections) and creating the supporting indexes:

-- Drop temp tables if exist

SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO

WITH D0 AS

-- D0 computes running demand as EndDemand

(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),

-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval

D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;

WITH S0 AS

-- S0 computes running supply as EndSupply

(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),

-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval

S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;

-- Indexing

CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);

The plans for populating the temporary tables and creating the indexes are shown in Figure 5.

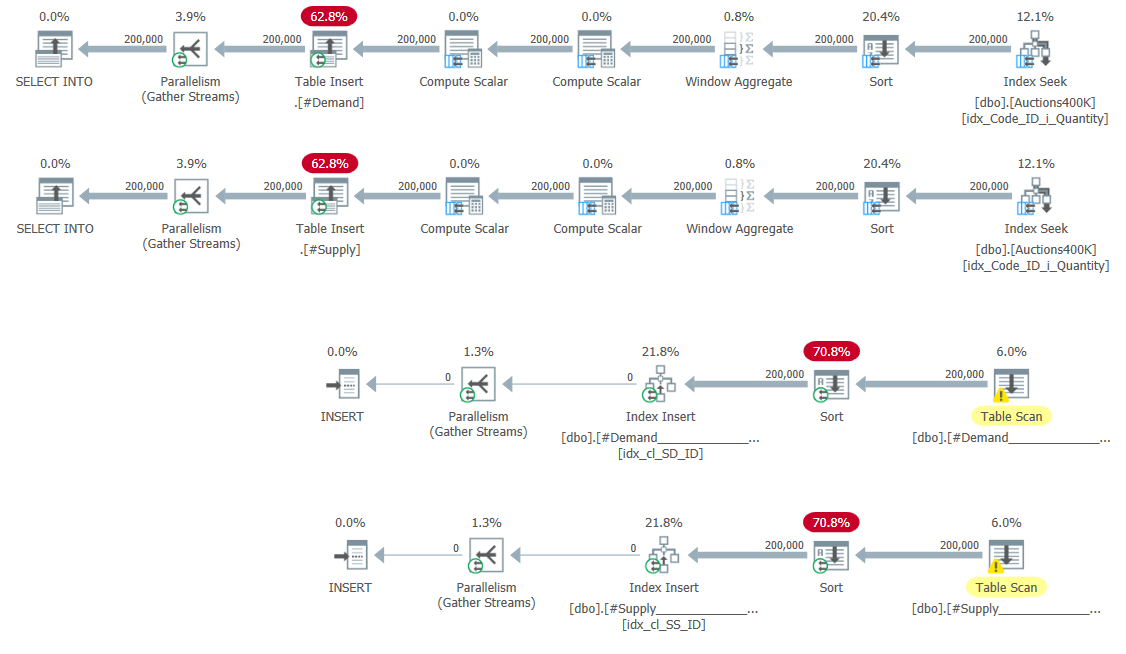
Figure 5: Query plans for populating temp tables and creating indexes

No surprises here.

Now to the final query. You might be tempted to use a single query with the aforementioned disjunction of two predicates, like so:

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >  D.StartDemand AND S.StartSupply < D.EndDemand);

The plan for this query is shown in Figure 6.

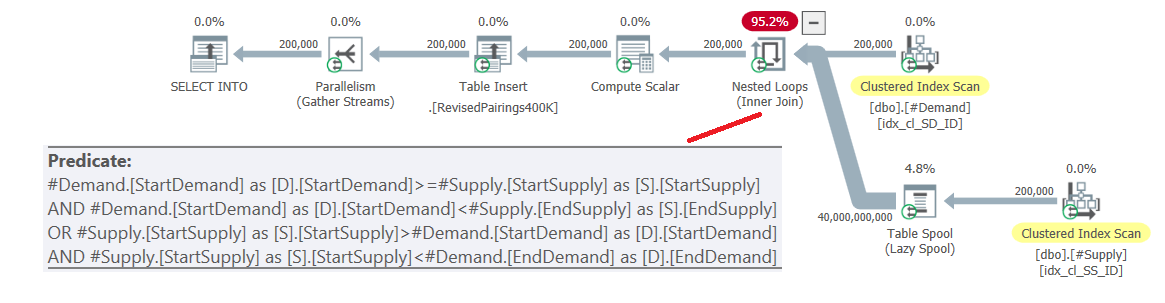
Figure 6: Query plan for final query using revised intersection test, try 1

The problem is that the optimizer doesn’t know how to break this logic into two separate activities, each handling a different predicate and utilizing the respective index efficiently. So, it ends up with a full cartesian product of the two sides, applying all predicates as residual predicates. With 200,000 demand rows and 200,000 supply rows, the join processes 40,000,000,000 rows.

The insightful trick used by Luca, Kamil, and possibly Daniel was to break the logic into two queries, unifying their results. That’s where using two disjoint predicates becomes important! You can use a UNION ALL operator instead of UNION, avoiding the unnecessary cost of looking for duplicates. Here’s the query implementing this approach:

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
    
UNION ALL

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

The plan for this query is shown in Figure 7.

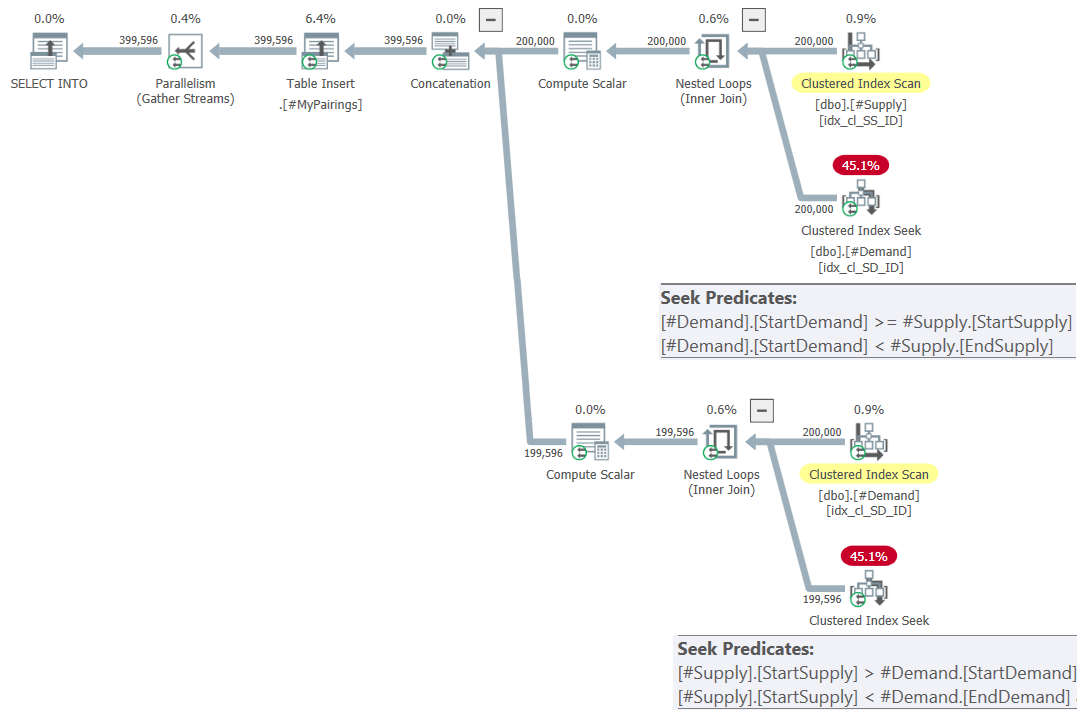
Figure 7: Query plan for final query using revised intersection test, try 2

This is just beautiful! Isn’t it? And because it’s so beautiful, here’s the entire solution from scratch, including the creation of temp tables, indexing, and the final query:

-- Drop temp tables if exist

SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO

WITH D0 AS

-- D0 computes running demand as EndDemand

(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),

-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval

D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;

WITH S0 AS

-- S0 computes running supply as EndSupply

(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),

-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval

S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID,
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;

-- Indexing

CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);

-- Trades are the overlapping segments of the intersecting intervals

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply

UNION ALL

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

As mentioned earlier, I’ll refer to this solution as revised intersections.

Kamil’s solution

Between Luca’s, Kamil’s, and Daniel’s solutions, Kamil’s was the fastest. Here’s Kamil’s complete solution:

SET NOCOUNT ON;
DROP TABLE IF EXISTS #supply, #demand;
GO

CREATE TABLE #demand
(
  DemandID           INT NOT NULL,
  DemandQuantity     DECIMAL(19, 6) NOT NULL,
  QuantityFromDemand DECIMAL(19, 6) NOT NULL,
  QuantityToDemand   DECIMAL(19, 6) NOT NULL
);
 
CREATE TABLE #supply
(
  SupplyID           INT NOT NULL,
  QuantityFromSupply DECIMAL(19, 6) NOT NULL,
  QuantityToSupply   DECIMAL(19,6) NOT NULL
);

WITH demand AS
(
  SELECT
    a.ID AS DemandID,
    a.Quantity AS DemandQuantity,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromDemand,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToDemand
  FROM dbo.Auctions AS a WHERE Code = 'D'
)
INSERT INTO #demand
(
  DemandID,
  DemandQuantity,
  QuantityFromDemand,
  QuantityToDemand
)
SELECT
  d.DemandID,
  d.DemandQuantity,
  d.QuantityFromDemand,
  d.QuantityToDemand
FROM demand AS d;

WITH supply AS
(
  SELECT
    a.ID AS SupplyID,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromSupply,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToSupply
  FROM dbo.Auctions AS a WHERE Code = 'S'
)
INSERT INTO #supply
(
  SupplyID,
  QuantityFromSupply,
  QuantityToSupply
)
SELECT
  s.SupplyID,
  s.QuantityFromSupply,
  s.QuantityToSupply
FROM supply AS s;

CREATE UNIQUE INDEX ix_1 ON #demand(QuantityFromDemand) 
  INCLUDE(DemandID, DemandQuantity, QuantityToDemand);
CREATE UNIQUE INDEX ix_1 ON #supply(QuantityFromSupply) 
  INCLUDE(SupplyID, QuantityToSupply);
CREATE NONCLUSTERED COLUMNSTORE INDEX nci ON #demand(DemandID) 
  WHERE DemandID is null;

DROP TABLE IF EXISTS #myPairings;

CREATE TABLE #myPairings
(
  DemandID      INT NOT NULL,
  SupplyID      INT NOT NULL,
  TradeQuantity DECIMAL(19, 6) NOT NULL
);

INSERT INTO #myPairings(DemandID, SupplyID, TradeQuantity) 
  SELECT
    d.DemandID,
    s.SupplyID, 
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 end
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity 
  FROM #demand AS d 
    INNER JOIN #supply AS s 
      ON (d.QuantityFromDemand < s.QuantityToSupply 
          AND s.QuantityFromSupply <= d.QuantityFromDemand)
 
  UNION ALL

  SELECT
    d.DemandID,
    s.SupplyID,
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 END
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity
  FROM #supply AS s 
    INNER JOIN #demand AS d 
      ON (s.QuantityFromSupply < d.QuantityToDemand 
          AND d.QuantityFromDemand < s.QuantityFromSupply);

As you can see, it’s very close to the revised intersections solution I covered.

The plan for the final query in Kamil’s solution is shown in Figure 8.

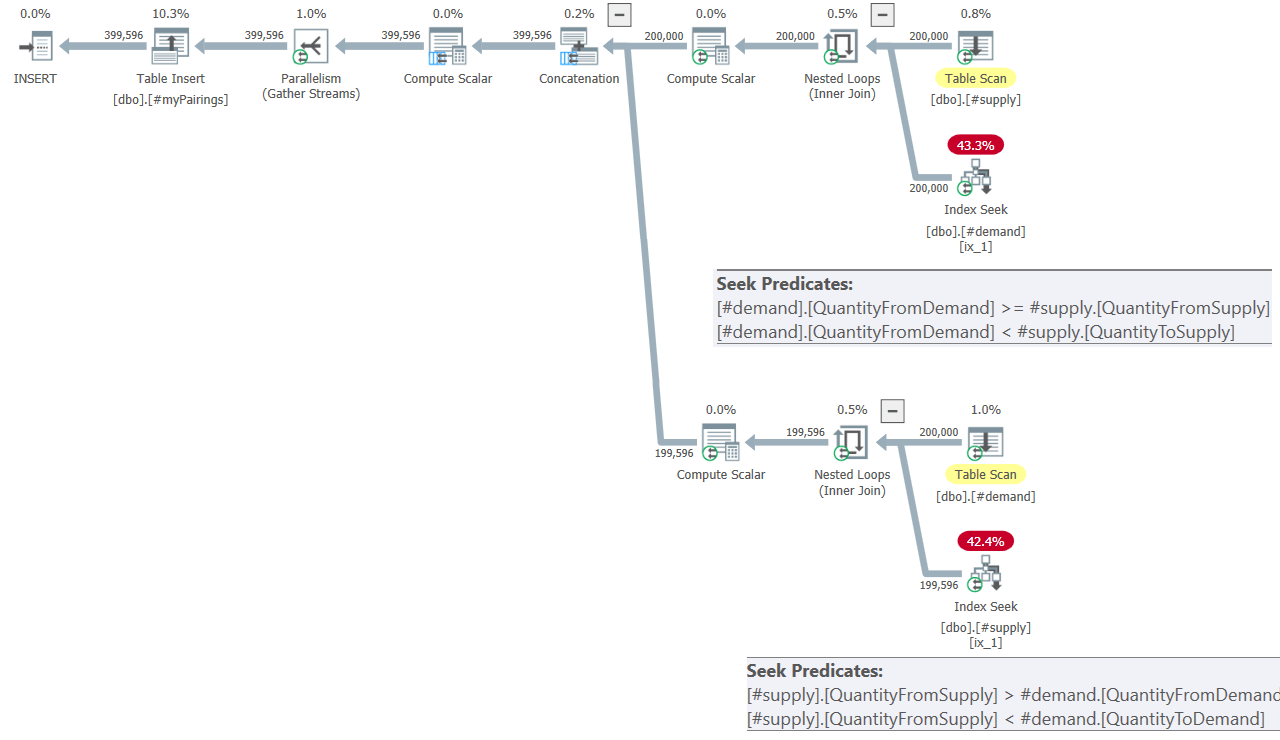
Figure 8: Query plan for final query in Kamil’s solution

The plan looks pretty similar to the one shown earlier in Figure 7.

Performance Test

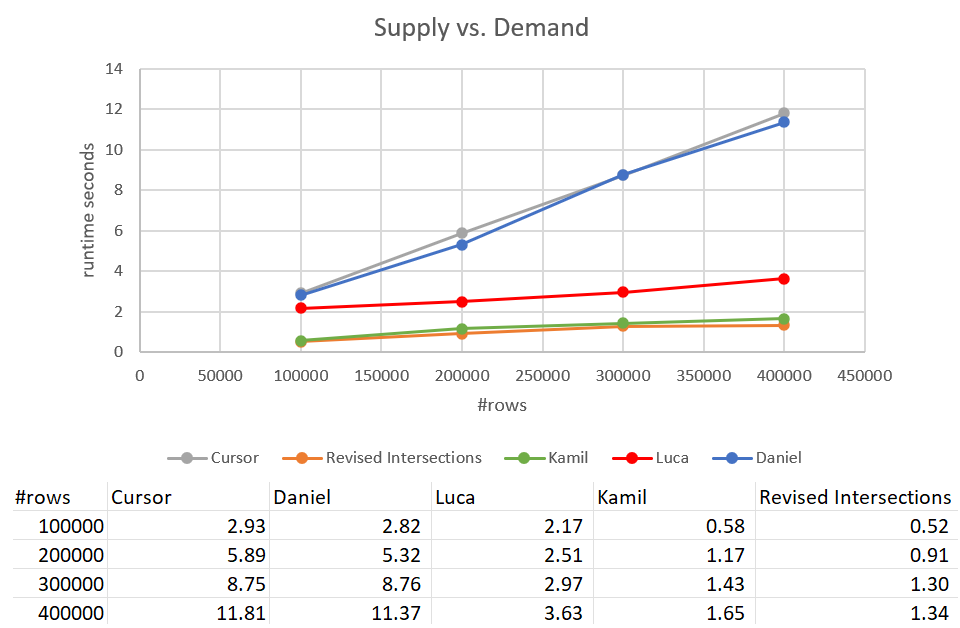
Recall that the classic intersections solution took 931 seconds to complete against an input with 400K rows. That’s 15 minutes! It’s much, much worse than the cursor solution, which took about 12 seconds to complete against the same input. Figure 9 has the performance numbers including the new solutions discussed in this article.

Figure 9: Performance test

As you can see, Kamil’s solution and the similar revised intersections solution took about 1.5 seconds to complete against the 400K-row input. That’s a pretty decent improvement compared to the original cursor-based solution. The main drawback of these solutions is the I/O cost. With a seek per row, for a 400K-row input, these solutions perform an excess of 1.35M reads. But it could also be considered a perfectly acceptable cost given the good run time and scaling you get.

What’s Next?

Our first attempt at solving the matching supply versus demand challenge relied on the classic interval intersection test and got a poor-performing plan with quadratic scaling. Much worse than the cursor-based solution. Based on insights from Luca, Kamil, and Daniel, using a revised interval intersection test, our second attempt was a significant improvement that utilizes indexing efficiently and performs better than the cursor-based solution. However, this solution involves a significant I/O cost. Next month I’ll continue exploring additional solutions.