Islands T-SQL Challenge

Recently, I was introduced to a new islands challenge by my friend Erland Sommarskog. It’s based on a question from a public database forum. The challenge itself isn’t complicated to handle when using well-known techniques, which primarily employ window functions. However, these techniques require explicit sorting despite the presence of a supporting index. This affects the scalability and response time of the solutions. Fond of challenges, I set out to find a solution to minimize the number of explicit Sort operators in the plan, or better yet, eliminate the need for those altogether. And I found such a solution.

I’ll start by presenting a generalized form of the challenge. I’ll then show two solutions based on known techniques, followed by the new solution. Finally, I’ll compare the performance of the different solutions.

I recommend you try to find a solution before implementing mine.

The challenge

I’ll present a generalized form of Erland’s original islands challenge.

Use the following code to create a table called T1 and populate it with a small set of sample data:

SET NOCOUNT ON;

USE tempdb;

DROP TABLE IF EXISTS dbo.T1

CREATE TABLE dbo.T1
(
  grp VARCHAR(10) NOT NULL,
  ord INT NOT NULL,
  val VARCHAR(10) NOT NULL,
  CONSTRAINT PK_T1 PRIMARY KEY(grp, ord)
);
GO

INSERT INTO dbo.T1(grp, ord, val) VALUES
  ('Group A', 1002, 'Y'),
  ('Group A', 1003, 'Y'),
  ('Group A', 1005, 'Y'),
  ('Group A', 1007, 'N'),
  ('Group A', 1011, 'N'),
  ('Group A', 1013, 'N'),
  ('Group A', 1017, 'Y'),
  ('Group A', 1019, 'Y'),
  ('Group A', 1023, 'N'),
  ('Group A', 1029, 'N'),
  ('Group B', 1001, 'X'),
  ('Group B', 1002, 'X'),
  ('Group B', 1003, 'Z'),
  ('Group B', 1005, 'Z'),
  ('Group B', 1008, 'Z'),
  ('Group B', 1013, 'Z'),
  ('Group B', 1021, 'Y'),
  ('Group B', 1034, 'Y');

The challenge is as follows:

Assuming partitioning based on the column grp and ordering based on the column ord, compute sequential row numbers starting with 1 within each consecutive group of rows with the same value in the val column. Following is the desired result for the given small set of sample data:

grp      ord   val  seqno
-------- ----- ---- ------
Group A  1002  Y    1
Group A  1003  Y    2
Group A  1005  Y    3
Group A  1007  N    1
Group A  1011  N    2
Group A  1013  N    3
Group A  1017  Y    1
Group A  1019  Y    2
Group A  1023  N    1
Group A  1029  N    2
Group B  1001  X    1
Group B  1002  X    2
Group B  1003  Z    1
Group B  1005  Z    2
Group B  1008  Z    3
Group B  1013  Z    4
Group B  1021  Y    1
Group B  1034  Y    2

Note the definition of the primary key constraint based on the composite key (grp, ord), which results in a clustered index based on the same key. This index can potentially support window functions partitioned by grp and ordered by ord.

To test the performance of your solution, you’ll need to populate the table with larger volumes of sample data. Use the following code to create the helper function GetNums:

CREATE FUNCTION dbo.GetNums(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  WITH
    L0 AS ( SELECT 1 AS c 
            FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
                        (1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
    L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
    L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
    L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
    Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
              FROM L3 )
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
     @low - 1 + rownum AS n
  FROM Nums
  ORDER BY rownum;
GO

Use the following code to populate T1, after changing the parameters representing the number of groups, number of rows per group and number of distinct values as you wish:

DECLARE 
  @numgroups AS INT = 1000,
  @rowspergroup AS INT = 10000, -- test with 1000 to 10000 here
  @uniquevalues AS INT = 5;

ALTER TABLE dbo.T1 DROP CONSTRAINT PK_T1;

TRUNCATE TABLE dbo.T1;

INSERT INTO dbo.T1 WITH(TABLOCK) (grp, ord, val)
  SELECT
    CAST(G.n AS VARCHAR(10)) AS grp,
    CAST(R.n AS INT) AS ord,
    CAST(ABS(CHECKSUM(NEWID())) % @uniquevalues + 1 AS VARCHAR(10)) AS val
  FROM dbo.GetNums(1, @numgroups) AS G
    CROSS JOIN dbo.GetNums(1, @rowspergroup) AS R;
    
ALTER TABLE dbo.T1 ADD CONSTRAINT PK_T1 PRIMARY KEY CLUSTERED(grp, ord);

In my performance tests, I populated the table with 1,000 groups, between 1,000 and 10,000 rows per group (so 1M to 10M rows), and 5 distinct values. I used a SELECT INTO statement to write the result into a temporary table.

My test machine has four logical CPUs, running SQL Server^® 2019 Enterprise.

I’ll assume you’re using an environment designed to support batch mode on row store either directly, e.g., using SQL Server 2019 Enterprise edition like mine, or indirectly, by creating a dummy columnstore index on the table.

Remember, extra points if you manage to come up with an efficient solution without explicit sorting in the plan. Good luck!

Is a Sort operator needed in the optimization of window functions?

Before I cover solutions, a bit of optimization background so what you’ll see in the query plans later will make more sense.

The most common techniques for solving islands tasks such as ours involve using some combination of aggregate and/or ranking window functions. SQL Server can process such window functions using either a series of older row mode operators (Segment, Sequence Project, Segment, Window Spool, Stream Aggregate) or the newer and usually more efficient batch mode Window Aggregate operator.

In both cases, the operators handling the window function’s calculation need to ingest the data ordered by the window partitioning and ordering elements. If you don’t have a supporting index, naturally SQL Server will need to introduce a Sort operator in the plan. For instance, if you have multiple window functions in your solution with more than one unique combination of partitioning and ordering, you’re bound to have explicit sorting in the plan. But what if you have only one unique combination of partitioning and ordering and a supporting index?

The older row mode method can rely on preordered data ingested from an index without the need for an explicit Sort operator in both serial and parallel modes. The newer batch mode operator eliminates much of the inefficiencies of the older row mode optimization and has the inherent benefits of batch mode processing. However, its current parallel implementation requires an intermediary batch mode parallel Sort operator even when a supporting index is present. Only its serial implementation can rely on index order without a Sort operator. This is all to say when the optimizer needs to choose a strategy to handle your window function, assuming you have a supporting index, it will generally be one of the following four options:

1. Row mode, serial, no sorting
2. Row mode, parallel, no sorting
3. Batch mode, serial, no sorting
4. Batch mode, parallel, sorting

Whichever one results in the lowest plan cost will be chosen, assuming of course prerequisites for parallelism and batch mode are met when considering those. Normally, for the optimizer to justify a parallel plan, the parallelism benefits need to outweigh the extra work like thread synchronization. With option 4 above, the parallelism benefits need to outweigh the usual extra work involved with parallelism, plus the extra sort.

While experimenting with different solutions to our challenge, I had cases where the optimizer chose option 2 above. It chose it despite the fact that the row mode method involves a few inefficiencies because the benefits in parallelism and no sorting resulted in a plan with a lower cost than the alternatives. In some of those cases, forcing a serial plan with a hint resulted in option 3 above, and in better performance.

With this background in mind, let’s look at solutions. I’ll start with two solutions relying on known techniques for islands tasks that cannot escape explicit sorting in the plan.

Solution based on known technique 1

Following is the first solution to our challenge, which is based on a technique that has been known for a while:

WITH C AS
(
  SELECT *,
    ROW_NUMBER() OVER(PARTITION BY grp ORDER BY ord) -
      ROW_NUMBER() OVER(PARTITION BY grp, val ORDER BY ord) AS island
  FROM dbo.T1
)
SELECT grp, ord, val, 
  ROW_NUMBER() OVER(PARTITION BY grp, val, island ORDER BY ord) AS seqno
FROM C;

I’ll refer to it as Known Solution 1.

The CTE called C is based on a query that computes two row numbers. The first (I’ll refer to it as rn1) is partitioned by grp and ordered by ord. The second (I’ll refer to it as rn2) is partitioned by grp and val and ordered by ord. Since rn1 has gaps between different groups of the same val and rn2 doesn’t, the difference between rn1 and rn2 (column called island) is a unique constant value for all rows with the same grp and val values. Following is the result of the inner query, including the results of the two-row number computations, which aren’t returned as separate columns:

grp      ord   val  rn1  rn2  island
-------- ----- ---- ---- ---- -------
Group A  1002  Y    1    1    0
Group A  1003  Y    2    2    0
Group A  1005  Y    3    3    0
Group A  1007  N    4    1    3
Group A  1011  N    5    2    3
Group A  1013  N    6    3    3
Group A  1017  Y    7    4    3
Group A  1019  Y    8    5    3
Group A  1023  N    9    4    5
Group A  1029  N    10   5    5
Group B  1001  X    1    1    0
Group B  1002  X    2    2    0
Group B  1003  Z    3    1    2
Group B  1005  Z    4    2    2
Group B  1008  Z    5    3    2
Group B  1013  Z    6    4    2
Group B  1021  Y    7    1    6
Group B  1034  Y    8    2    6

What’s left for the outer query to do is to compute the result column seqno using the ROW_NUMBER function, partitioned by grp, val, and island, and ordered by ord, generating the desired result.

Note you can get the same island value for different val values within the same partition, such as in the output above. This is why it’s important to use grp, val, and island as the window partitioning elements and not grp and island alone.

Similarly, if you’re dealing with an islands task requiring you to group the data by the island and compute group aggregates, you would group the rows by grp, val, and island. But this isn’t the case with our challenge. Here you were tasked with just computing row numbers independently for each island.

Figure 1 has the default plan that I got for this solution on my machine after populating the table with 10M rows.

Figure 1: Parallel plan for Known Solution 1

The computation of rn1 can rely on index order. So, the optimizer chose the no sort + parallel row mode strategy for this one (first Segment and Sequence Project operators in the plan). Since the computations of both rn2 and seqno use their own unique combinations of partitioning and ordering elements, explicit sorting is unavoidable for those irrespective of the strategy used. So, the optimizer chose the sort + parallel batch mode strategy for both. This plan involves two explicit Sort operators.

In my performance test, it took this solution 3.68 seconds to complete against 1M rows and 43.1 seconds against 10M rows.

As mentioned, I tested all solutions also by forcing a serial plan (with a MAXDOP 1 hint). The serial plan for this solution is shown in Figure 1.

Figure 2: Serial plan for Known Solution 1

As expected, this time also the computation of rn1 uses the batch mode strategy without a preceding Sort operator, but the plan still has two Sort operators for the subsequent row number computations. The serial plan performed worse than the parallel one on my machine with all input sizes I tested, taking 4.54 seconds to complete with 1M rows and 61.5 seconds with 10M rows.

Solution based on known technique 2

The second solution I’ll present is based on a brilliant technique for island detection I learned from Paul White a few years ago. Following is the complete solution code based on this technique:

WITH C1 AS
(
  SELECT *,
    CASE
      WHEN val = LAG(val) OVER(PARTITION BY grp ORDER BY ord) THEN 0
      ELSE 1
    END AS isstart
  FROM dbo.T1
),
C2 AS
(
  SELECT *,
    SUM(isstart) OVER(PARTITION BY grp ORDER BY ord ROWS UNBOUNDED PRECEDING) AS island
  FROM C1
)
SELECT grp, ord, val, 
  ROW_NUMBER() OVER(PARTITION BY grp, island ORDER BY ord) AS seqno
FROM C2;

I’ll refer to this solution as Known Solution 2.

The query defining the CTE C1 computes uses a CASE expression and the LAG window function (partitioned by grp and ordered by ord) to compute a result column called isstart. This column has the value 0 when the current val value is the same as the previous and 1 otherwise. In other words, it’s 1 when the row is the first in an island and 0 otherwise.

Following is the output of the query defining C1:

grp      ord   val  isstart
-------- ----- ---- --------
Group A  1002  Y    1
Group A  1003  Y    0
Group A  1005  Y    0
Group A  1007  N    1
Group A  1011  N    0
Group A  1013  N    0
Group A  1017  Y    1
Group A  1019  Y    0
Group A  1023  N    1
Group A  1029  N    0
Group B  1001  X    1
Group B  1002  X    0
Group B  1003  Z    1
Group B  1005  Z    0
Group B  1008  Z    0
Group B  1013  Z    0
Group B  1021  Y    1
Group B  1034  Y    0

The magic as far as island detection is concerned happens in the CTE C2. The query defining it computes an island identifier using the SUM window function (also partitioned by grp and ordered by ord) applied to the isstart column. The result column with the island identifier is called island. Within each partition, you get 1 for the first island, 2 for the second island, and so on. So, the combination of columns grp and island is an island identifier, which you can use in islands tasks that involve grouping by island when relevant.

Following is the output of the query defining C2:

grp      ord   val  isstart  island
-------- ----- ---- -------- -------
Group A  1002  Y    1        1
Group A  1003  Y    0        1
Group A  1005  Y    0        1
Group A  1007  N    1        2
Group A  1011  N    0        2
Group A  1013  N    0        2
Group A  1017  Y    1        3
Group A  1019  Y    0        3
Group A  1023  N    1        4
Group A  1029  N    0        4
Group B  1001  X    1        1
Group B  1002  X    0        1
Group B  1003  Z    1        2
Group B  1005  Z    0        2
Group B  1008  Z    0        2
Group B  1013  Z    0        2
Group B  1021  Y    1        3
Group B  1034  Y    0        3

Lastly, the outer query computes the desired result column seqno with a ROW_NUMBER function, partitioned by grp and island, and ordered by ord. Notice this combination of partitioning and ordering elements is different from the one used by the previous window functions. Whereas the computation of the first two window functions can potentially rely on index order, the last can’t.

Figure 3 has the default plan that I got for this solution.

Figure 3: Parallel plan for Known Solution 2

As you can see in the plan, the computation of the first two window functions uses the no sort + parallel row mode strategy, and the computation of the last uses the sort + parallel batch mode strategy.

The run times I got for this solution ranged from 2.57 seconds against 1M rows to 46.2 seconds against 10M rows.

When forcing serial processing, I got the plan shown in Figure 4.

Figure 4: Serial plan for Known Solution 2

As expected, this time all window function computations rely on the batch mode strategy. The first two without preceding sorting, and the last with. Both the parallel plan and the serial one involved one explicit Sort operator. The serial plan performed better than the parallel plan on my machine with the input sizes I tested. The run times I got for the forced serial plan ranged from 1.75 seconds against 1M rows to 21.7 seconds against 10M rows.

Solution based on new technique

When Erland introduced this challenge in a private forum, people were skeptical of the possibility of solving it with a query that had been optimized with a plan without explicit sorting. That’s all I needed to hear to motivate me. So, here’s what I came up with:

WITH C1 AS
(
  SELECT *,
    ROW_NUMBER() OVER(PARTITION BY grp ORDER BY ord) AS rn,
    LAG(val) OVER(PARTITION BY grp ORDER BY ord) AS prev 
  FROM dbo.T1
),
C2 AS
(
  SELECT *,
    MAX(CASE WHEN val = prev THEN NULL ELSE rn END)
      OVER(PARTITION BY grp ORDER BY ord ROWS UNBOUNDED PRECEDING) AS firstrn
  FROM C1
)
SELECT grp, ord, val, rn - firstrn + 1 AS seqno
FROM C2;

The solution uses three window functions: LAG, ROW_NUMBER and MAX. The important thing here is all three are based on grp partitioning and ord ordering, which is aligned with the supporting index key order.

The query defining the CTE C1 uses the ROW_NUMBER function to compute row numbers (rn column), and the LAG function to return the previous val value (prev column).

Here’s the output of the query defining C1:

grp      ord   val  rn  prev
-------- ----- ---- --- -----
Group A  1002  Y    1   NULL
Group A  1003  Y    2   Y
Group A  1005  Y    3   Y
Group A  1007  N    4   Y
Group A  1011  N    5   N
Group A  1013  N    6   N
Group A  1017  Y    7   N
Group A  1019  Y    8   Y
Group A  1023  N    9   Y
Group A  1029  N    10  N
Group B  1001  X    1   NULL
Group B  1002  X    2   X
Group B  1003  Z    3   X
Group B  1005  Z    4   Z
Group B  1008  Z    5   Z
Group B  1013  Z    6   Z
Group B  1021  Y    7   Z
Group B  1034  Y    8   Y

Notice when val and prev are the same, it’s not the first row in the island, otherwise it is.

Based on this logic, the query defining the CTE C2 uses a CASE expression that returns rn when the row is the first in an island and NULL otherwise. The code then applies the MAX window function to the result of the CASE expression, returning the first rn of the island (firstrn column).

Here’s the output of the query defining C2, including the output of the CASE expression:

grp      ord   val  rn  prev  CASE  firstrn
-------- ----- ---- --- ----- ----- --------
Group A  1002  Y    1   NULL  1     1
Group A  1003  Y    2   Y     NULL  1
Group A  1005  Y    3   Y     NULL  1
Group A  1007  N    4   Y     4     4
Group A  1011  N    5   N     NULL  4
Group A  1013  N    6   N     NULL  4
Group A  1017  Y    7   N     7     7
Group A  1019  Y    8   Y     NULL  7
Group A  1023  N    9   Y     9     9
Group A  1029  N    10  N     NULL  9
Group B  1001  X    1   NULL  1     1
Group B  1002  X    2   X     NULL  1
Group B  1003  Z    3   X     3     3
Group B  1005  Z    4   Z     NULL  3
Group B  1008  Z    5   Z     NULL  3
Group B  1013  Z    6   Z     NULL  3
Group B  1021  Y    7   Z     7     7
Group B  1034  Y    8   Y     NULL  7

What’s left for the outer query is to compute the desired result column seqno as rn minus firstrn plus 1.

Figure 5 has the default parallel plan I got for this solution when testing it using a SELECT INTO statement, writing the result into a temporary table.

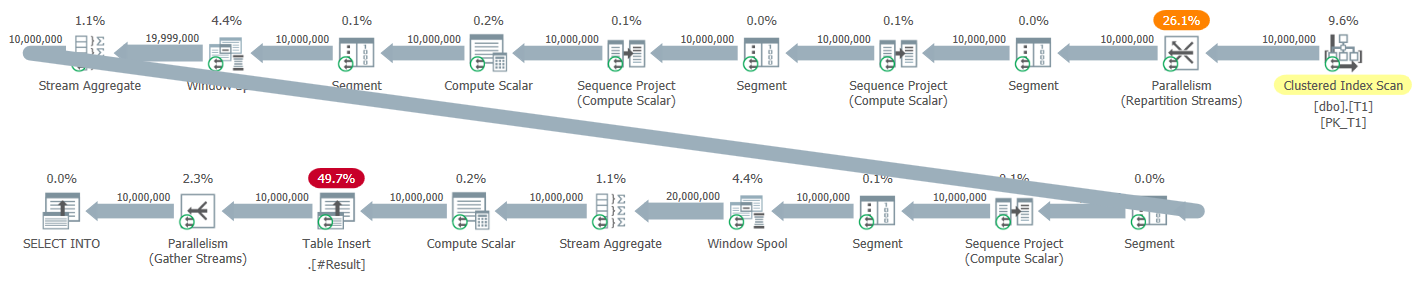Figure 5: Parallel plan for a new solution

There are no explicit sort operators in this plan. However, all three window functions are computed using the no sort + parallel row mode strategy, so we’re missing the benefits of batch processing. The run times I got for this solution with the parallel plan ranged from 2.47 seconds against 1M rows and 41.4 against 10M rows.

Here, there’s quite high likelihood for a serial plan with batch processing to do significantly better, especially when the machine doesn’t have many CPUs. Recall I’m testing my solutions against a machine with 4 logical CPUs. Figure 6 has the plan I got for this solution when forcing serial processing.

Figure 6: Serial plan for a new solution

All three window functions use the no sort + serial batch mode strategy. And the results are quite impressive. This solution run times ranged from 0.5 seconds against 1M rows and 5.49 seconds against 10M rows. What’s also curious about this solution is when testing it as a normal SELECT statement (with results discarded) as opposed to a SELECT INTO statement, SQL Server chose the serial plan by default. With the other two solutions, I got a parallel plan by default both with SELECT and with SELECT INTO.

See the next section for the complete performance test results.

Performance comparison

Here’s the code I used to test the three solutions, of course uncommenting the MAXDOP 1 hint to test the serial plans:

-- Test Known Solution 1

DROP TABLE IF EXISTS #Result;

WITH C AS
(
  SELECT *,
    ROW_NUMBER() OVER(PARTITION BY grp ORDER BY ord) -
      ROW_NUMBER() OVER(PARTITION BY grp, val ORDER BY ord) AS island
  FROM dbo.T1
)
SELECT grp, ord, val, 
  ROW_NUMBER() OVER(PARTITION BY grp, val, island ORDER BY ord) AS seqno
INTO #Result
FROM C
/* OPTION(MAXDOP 1) */; -- uncomment for serial test
GO

-- Test Known Solution 2

DROP TABLE IF EXISTS #Result;

WITH C1 AS
(
  SELECT *,
    CASE
      WHEN val = LAG(val) OVER(PARTITION BY grp ORDER BY ord) THEN 0
      ELSE 1
    END AS isstart
  FROM dbo.T1
),
C2 AS
(
  SELECT *,
    SUM(isstart) OVER(PARTITION BY grp ORDER BY ord ROWS UNBOUNDED PRECEDING) AS island
  FROM C1
)
SELECT grp, ord, val, 
  ROW_NUMBER() OVER(PARTITION BY grp, island ORDER BY ord) AS seqno
INTO #Result
FROM C2
/* OPTION(MAXDOP 1) */;
GO

-- Test New Solution

DROP TABLE IF EXISTS #Result;

WITH C1 AS
(
  SELECT *,
    ROW_NUMBER() OVER(PARTITION BY grp ORDER BY ord) AS rn,
    LAG(val) OVER(PARTITION BY grp ORDER BY ord) AS prev 
  FROM dbo.T1
),
C2 AS
(
  SELECT *,
    MAX(CASE WHEN val = prev THEN NULL ELSE rn END)
      OVER(PARTITION BY grp ORDER BY ord ROWS UNBOUNDED PRECEDING) AS firstrn
  FROM C1
)
SELECT grp, ord, val, rn - firstrn + 1 AS seqno
INTO #Result
FROM C2
/* OPTION(MAXDOP 1) */;

Figure 7 has the run times of both the parallel and serial plans for all solutions against different input sizes.

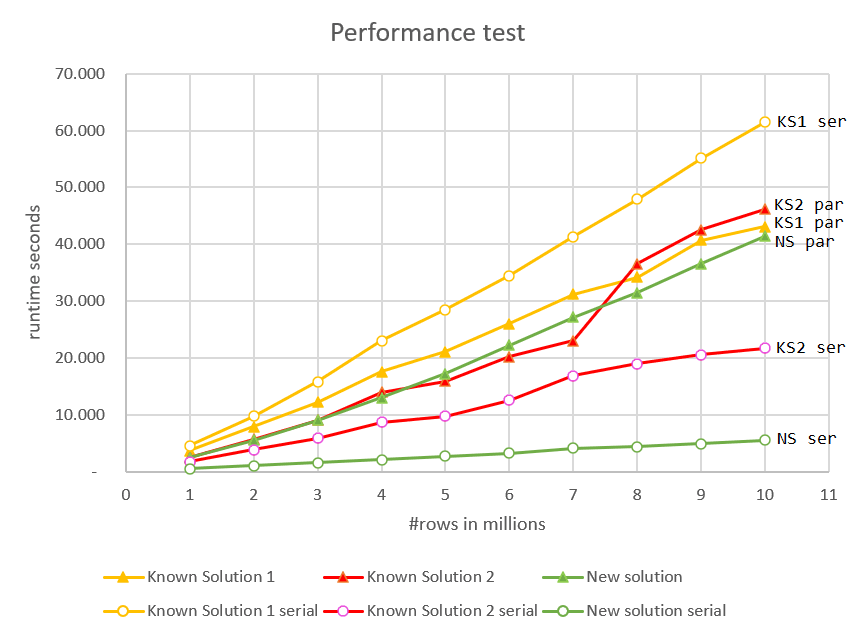Figure 7: Performance comparison

The new solution, using serial mode, is the clear winner. It has great performance, linear scaling, and immediate response time.

Conclusion

Islands tasks are quite common in real life. Many of them involve both identifying islands and grouping the data by the island. Erland’s islands challenge, which was the focus of this article, is a bit more unique because it doesn’t involve grouping but instead sequencing each island’s rows with row numbers.

I presented two solutions based on known techniques for identifying islands. The problem with both is they result in plans involving explicit sorting, which negatively affects the performance, scalability, and response time of the solutions. I also presented a new technique that resulted in a plan with no sorting at all. The serial plan for this solution, which uses a no sort + serial batch mode strategy, has excellent performance, linear scaling, and immediate response time. It’s unfortunate, at least for now, we can’t have a no sort + parallel batch mode strategy for handling window functions.