This article is the sixth part in a series about table expressions. Last month in Part 5 I covered the logical treatment of nonrecursive CTEs. This month I cover the logical treatment of recursive CTEs. I describe T-SQL’s support for recursive CTEs, as well as standard elements that are not yet supported by T-SQL. I do provide logically equivalent T-SQL workarounds for the unsupported elements.
Sample data
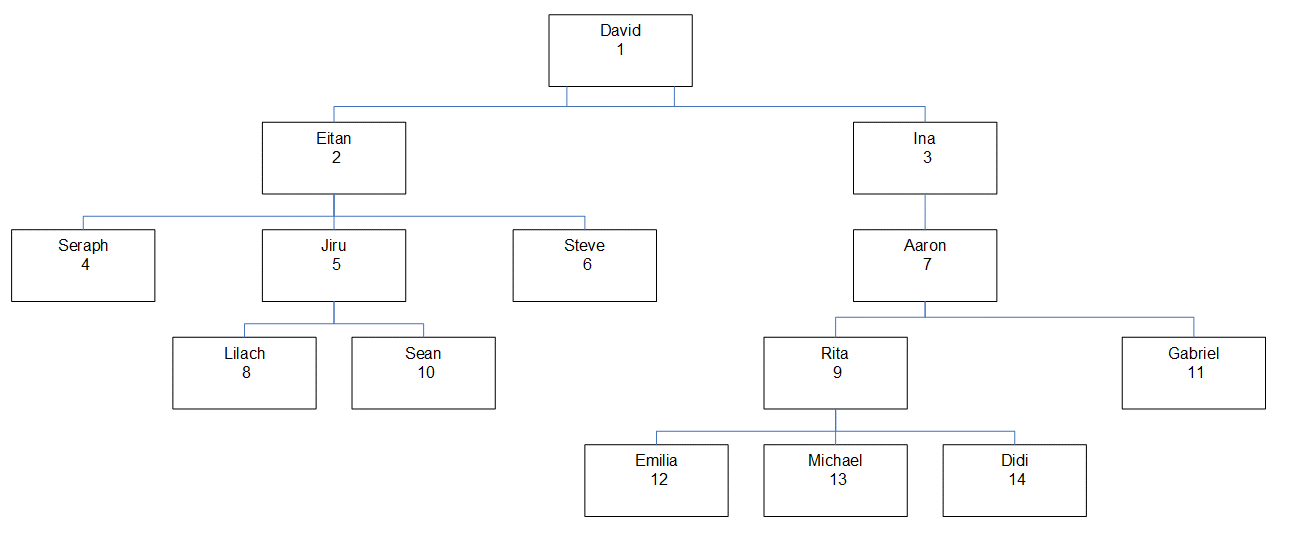
For sample data I’ll use a table called Employees, which holds a hierarchy of employees. The empid column represents the employee ID of the subordinate (the child node), and the mgrid column represents the employee ID of the manager (the parent node). Use the following code to create and populate the Employees table in the tempdb database:
SET NOCOUNT ON;
USE tempdb;
DROP TABLE IF EXISTS dbo.Employees;
GO
CREATE TABLE dbo.Employees
(
empid INT NOT NULL
CONSTRAINT PK_Employees PRIMARY KEY,
mgrid INT NULL
CONSTRAINT FK_Employees_Employees REFERENCES dbo.Employees,
empname VARCHAR(25) NOT NULL,
salary MONEY NOT NULL,
CHECK (empid <> mgrid)
);
INSERT INTO dbo.Employees(empid, mgrid, empname, salary)
VALUES(1, NULL, 'David' , $10000.00),
(2, 1, 'Eitan' , $7000.00),
(3, 1, 'Ina' , $7500.00),
(4, 2, 'Seraph' , $5000.00),
(5, 2, 'Jiru' , $5500.00),
(6, 2, 'Steve' , $4500.00),
(7, 3, 'Aaron' , $5000.00),
(8, 5, 'Lilach' , $3500.00),
(9, 7, 'Rita' , $3000.00),
(10, 5, 'Sean' , $3000.00),
(11, 7, 'Gabriel', $3000.00),
(12, 9, 'Emilia' , $2000.00),
(13, 9, 'Michael', $2000.00),
(14, 9, 'Didi' , $1500.00);
CREATE UNIQUE INDEX idx_unc_mgrid_empid
ON dbo.Employees(mgrid, empid)
INCLUDE(empname, salary);
Observe that the root of the employee hierarchy—the CEO—has a NULL in the mgrid column. All the rest of the employees do have a manager, so their mgrid column is set to the employee ID of their manager.
Figure 1 has a graphical depiction of the employee hierarchy, showing the employee name, ID, and its location in the hierarchy.
Figure 1: Employee hierarchy
Recursive CTEs
Recursive CTEs have many use cases. A classic category of uses has to do with handling of graph structures, like our employee hierarchy. Tasks involving graphs often require traversing arbitrary length paths. For example, given the employee ID of some manager, return the input employee, as well as all subordinates of the input employee in all levels; i.e., direct and indirect subordinates. If you had a known small limit on the number of levels that you might need to follow (the degree of the graph), you could use a query with a join per level of subordinates. However, if the degree of the graph is potentially high, at some point it becomes impractical to write a query with many joins. Another option is to use imperative iterative code, but such solutions tend to be lengthy. This is where recursive CTEs really shine—they enable you to use declarative, concise and intuitive solutions.
I’ll start with the basics of recursive CTEs before I get to the more interesting stuff where I cover searching and cycling capabilities.
Remember that the syntax of a query against a CTE is as follows:
AS
(
<table expression>
)
<outer query>;
Here I show one CTE defined using the WITH clause, but as you know, you can define multiple CTEs separated by commas.
In regular, nonrecursive, CTEs, the inner table expression is based on a query that is evaluated only once. In recursive CTEs, the inner table expression is based on typically two queries known as members, though you can have more than two to handle some specialized needs. The members are separated typically by a UNION ALL operator to indicate that their results are unified.
A member can be an anchor member—meaning that it is evaluated only once; or it can be a recursive member—meaning that it is evaluated repeatedly, until it returns an empty result set. Here’s the syntax of a query against a recursive CTE that is based on one anchor member and one recursive member:
AS
(
<anchor member>
UNION ALL
<recursive member>
)
<outer query>;
What makes a member recursive is having a reference to the CTE name. This reference represents the last execution’s result set. In the first execution of the recursive member, the reference to the CTE name represents the anchor member’s result set. In the Nth execution, where N > 1, the reference to the CTE name represents the result set of the (N – 1) execution of the recursive member. As mentioned, once the recursive member returns an empty set, its not executed again. A reference to the CTE name in the outer query represents the unified result sets of the single execution of the anchor member, and all of the executions of the recursive member.
The following code implements the aforementioned task of returning the subtree of employees for a given input manager, passing employee ID 3 as the root employee in this example:
DECLARE @root AS INT = 3;
WITH C AS
(
SELECT empid, mgrid, empname
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
)
SELECT empid, mgrid, empname
FROM C;
The anchor query is executed only once, returning the row for the input root employee (employee 3 in our case).
The recursive query joins the set of employees from the previous level—represented by the reference to the CTE name, aliased as M for managers—with their direct subordinates from the Employees table, aliased as S for subordinates. The join predicate is S.mgrid = M.empid, meaning that the subordinate’s mgrid value is equal to the manager’s empid value. The recursive query gets executed four times as follows:
- Return subordinates of employee 3; output: employee 7
- Return subordinates of employee 7; output: employees 9 and 11
- Return subordinates of employees 9 and 11; output: 12, 13 and 14
- Return subordinates of employees 12, 13 and 14; output: empty set; recursion stops
The reference to the CTE name in the outer query represents the unified results of the single execution of the anchor query (employee 3) with the results of all of the executions of the recursive query (employees 7, 9, 11, 12, 13 and 14). This code generates the following output:
empid mgrid empname ------ ------ -------- 3 1 Ina 7 3 Aaron 9 7 Rita 11 7 Gabriel 12 9 Emilia 13 9 Michael 14 9 Didi
A common problem in programming solutions is runaway code like infinite loops typically caused by a bug. With recursive CTEs, a bug could lead to a runway execution of the recursive member. For instance, suppose that in our solution for returning the subordinates of an input employee, you had a bug in the recursive member’s join predicate. Instead of using ON S.mgrid = M.empid, you used ON S.mgrid = S.mgrid, like so:
DECLARE @root AS INT = 3;
WITH C AS
(
SELECT empid, mgrid, empname
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = S.mgrid
)
SELECT empid, mgrid, empname
FROM C;
Given at least one employee with a nonnull manager ID present in the table, the execution of the recursive member will keep returning a nonempty result. Remember that the implicit termination condition for the recursive member is when its execution returns an empty result set. If it returns a nonempty result set, SQL Server executes it again. You realize that if SQL Server didn’t have a mechanism to limit the recursive executions, it would just keep executing the recursive member repeatedly forever. As a safety measure, T-SQL supports a MAXRECURSION query option that limits the maximum allowed number of executions of the recursive member. By default, this limit is set to 100, but you can change it to any nonnegative SMALLINT value, with 0 representing no limit. Setting the max recursion limit to a positive value N means that the N + 1 attempted execution of the recursive member is aborted with an error. For example, running the above buggy code as is means that you rely on the default max recursion limit of 100, so the 101st execution of the recursive member fails:
empid mgrid empname ------ ------ -------- 3 1 Ina 2 1 Eitan 3 1 Ina ...
The statement terminated. The maximum recursion 100 has been exhausted before statement completion.
Say that in your organization it is safe to assume that the employee hierarchy will not exceed 6 management levels. You can reduce the max recursion limit from 100 to a much smaller number, such as 10 to be on the safe side, like so:
DECLARE @root AS INT = 3;
WITH C AS
(
SELECT empid, mgrid, empname
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = S.mgrid
)
SELECT empid, mgrid, empname
FROM C
OPTION (MAXRECURSION 10);
Now if there’s a bug resulting in a runaway execution of the recursive member, it will be discovered at the 11th attempted execution of the recursive member instead of at the 101st execution:
empid mgrid empname ------ ------ -------- 3 1 Ina 2 1 Eitan 3 1 Ina ...
The statement terminated. The maximum recursion 10 has been exhausted before statement completion.
It’s important to note that the max recursion limit should be used mainly as a safety measure to abort the execution of buggy runaway code. Remember that when the limit is exceeded, the execution of the code is aborted with an error. You shouldn’t use this option to limit the number of levels to visit for filtering purposes. You don’t want an error to be generated when there’s no problem with the code.
For filtering purposes, you can limit the number of levels to visit programmatically. You define a column called lvl that tracks the level number of the current employee compared to the input root employee. In the anchor query you set the lvl column to the constant 0. In the recursive query you set it to the manager’s lvl value plus 1. To filter as many levels below the input root as @maxlevel, add the predicate M.lvl < @maxlevel to the ON clause of the recursive query. For example, the following code returns employee 3 and two levels of subordinates of employee 3:
DECLARE @root AS INT = 3, @maxlevel AS INT = 2;
WITH C AS
(
SELECT empid, mgrid, empname, 0 AS lvl
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname, M.lvl + 1 AS lvl
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
AND M.lvl < @maxlevel
)
SELECT empid, mgrid, empname, lvl
FROM C;
This query generates the following output:
empid mgrid empname lvl ------ ------ -------- ---- 3 1 Ina 0 7 3 Aaron 1 9 7 Rita 2 11 7 Gabriel 2
Standard SEARCH and CYCLE clauses
The ISO/IEC SQL standard defines two very powerful options for recursive CTEs. One is a clause called SEARCH that controls the recursive search order, and another is a clause called CYCLE that identifies cycles in the traversed paths. Here’s the standard syntax for the two clauses:
Function
Specify the generation of ordering and cycle detection information in the result of recursive query expressions.
Format
<with list element> ::=
<query name> [ <left paren> <with column list> <right paren> ]
AS <table subquery> [ <search or cycle clause> ]
<search or cycle clause> ::=
<search clause> | <cycle clause> | <search clause> <cycle clause>
<search clause> ::=
SEARCH <recursive search order> SET <sequence column>
<recursive search order> ::=
DEPTH FIRST BY <column name list> | BREADTH FIRST BY <column name list>
<sequence column> ::= <column name>
<cycle clause> ::=
CYCLE <cycle column list> SET <cycle mark column> TO <cycle mark value>
DEFAULT <non-cycle mark value> USING <path column>
<cycle column list> ::= <cycle column> [ { <comma> <cycle column> }... ]
<cycle column> ::= <column name>
<cycle mark column> ::= <column name>
<path column> ::= <column name>
<cycle mark value> ::= <value expression>
<non-cycle mark value> ::= <value expression>
At the time of writing T-SQL doesn’t support these options, but in the following links you can find feature improvement requests asking for their inclusion in T-SQL in the future, and vote for them:
- Add support for ISO/IEC SQL SEARCH clause to recursive CTEs in T-SQL
- Add support for ISO/IEC SQL CYCLE clause to recursive CTEs in T-SQL
In the following sections I’ll describe the two standard options and also provide logically equivalent alternative solutions that are currently available in T-SQL.
SEARCH clause
The standard SEARCH clause defines the recursive search order as BREADTH FIRST or DEPTH FIRST by some specified ordering column(s), and creates a new sequence column with the ordinal positions of the visited nodes. You specify BREADTH FIRST to search first across each level (breadth) and then down the levels (depth). You specify DEPTH FIRST to search first down (depth) and then across (breadth).
You specify the SEARCH clause right before the outer query.
I’ll start with an example for breadth first recursive search order. Just remember that this feature is not available in T-SQL, so you won’t be able to actually run the examples that use the standard clauses in SQL Server or Azure SQL Database. The following code returns the subtree of employee 1, asking for a breadth first search order by empid, creating a sequence column called seqbreadth with the ordinal positions of the visited nodes:
DECLARE @root AS INT = 1;
WITH C AS
(
SELECT empid, mgrid, empname
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
)
SEARCH BREADTH FIRST BY empid SET seqbreadth
--------------------------------------------
SELECT empid, mgrid, empname, seqbreadth
FROM C
ORDER BY seqbreadth;
Here’s the desired output of this code:
empid mgrid empname seqbreadth ------ ------ -------- ----------- 1 NULL David 1 2 1 Eitan 2 3 1 Ina 3 4 2 Seraph 4 5 2 Jiru 5 6 2 Steve 6 7 3 Aaron 7 8 5 Lilach 8 9 7 Rita 9 10 5 Sean 10 11 7 Gabriel 11 12 9 Emilia 12 13 9 Michael 13 14 9 Didi 14
Don’t get confused by the fact that the seqbreadth values seem to be identical to the empid values. That’s just by chance as a result of the way that I manually assigned the empid values in the sample data that I created.
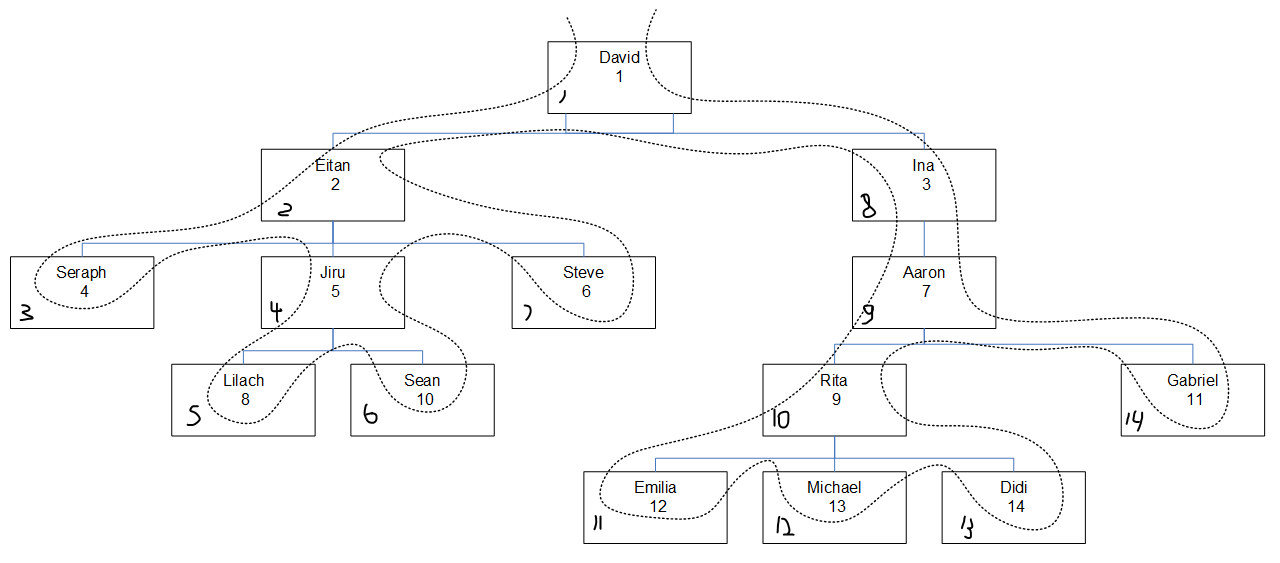
Figure 2 has a graphical depiction of the employee hierarchy, with a dotted line showing the breadth first order in which the nodes were searched. The empid values appear right below the employee names, and the assigned seqbreadth values appear at the bottom left corner of each box.
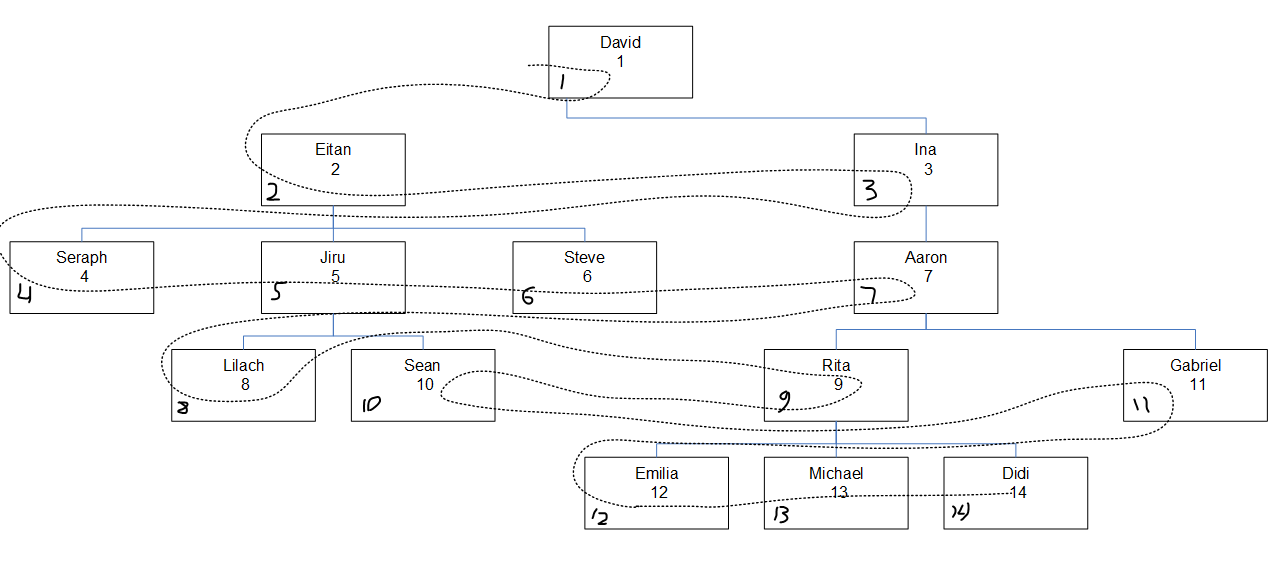Figure 2: Search breadth first
What’s interesting to note here is that within each level, the nodes are searched based on the specified column order (empid in our case) irrespective of the node’s parent association. For example, notice that in the fourth level Lilach is accessed first, Rita second, Sean third and Gabriel last. That’s because among all employees in the fourth level, that’s their order based on their empid values. It’s not like Lilach and Sean are supposed to be searched consecutively because they are direct subordinates of the same manager, Jiru.
It’s fairly simple to come up with a T-SQL solution that provides the logical equivalent of the standard SAERCH DEPTH FIRST option. You create a column called lvl like I showed earlier to track the level of the node with respect to the root (0 for the first level, 1 for the second, and so on). Then you compute the desired result sequence column in the outer query using a ROW_NUMBER function. As the window ordering you specify lvl first, and then the desired ordering column (empid in our case). Here’s the complete solution’s code:
DECLARE @root AS INT = 1;
WITH C AS
(
SELECT empid, mgrid, empname, 0 AS lvl
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname, M.lvl + 1 AS lvl
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
)
SELECT empid, mgrid, empname,
ROW_NUMBER() OVER(ORDER BY lvl, empid) AS seqbreadth
FROM C
ORDER BY seqbreadth;
Next, let’s examine the DEPTH FIRST search order. According to the standard, the following code should return the subtree of employee 1, asking for a depth first search order by empid, creating a sequence column called seqdepth with the ordinal positions of the searched nodes:
DECLARE @root AS INT = 1;
WITH C AS
(
SELECT empid, mgrid, empname
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
)
SEARCH DEPTH FIRST BY empid SET seqdepth
----------------------------------------
SELECT empid, mgrid, empname, seqdepth
FROM C
ORDER BY seqdepth;
Following is the desired output of this code:
empid mgrid empname seqdepth ------ ------ -------- --------- 1 NULL David 1 2 1 Eitan 2 4 2 Seraph 3 5 2 Jiru 4 8 5 Lilach 5 10 5 Sean 6 6 2 Steve 7 3 1 Ina 8 7 3 Aaron 9 9 7 Rita 10 12 9 Emilia 11 13 9 Michael 12 14 9 Didi 13 11 7 Gabriel 14
Looking at the desired query output it’s probably hard to figure out why the sequence values were assigned the way they were. Figure 3 should help. It has a graphical depiction of the employee hierarchy, with a dotted line reflecting the depth first search order, with the assigned sequence values in the bottom left corner of each box.
Figure 3: Search depth first
Coming up with a T-SQL solution that provides the logical equivalent to the standard SEARCH DEPTH FIRST option is a bit tricky, yet doable. I’ll describe the solution in two steps.
In Step 1, for each node you compute a binary sort path that is made of a segment per ancestor of the node, with each segment reflecting the sort position of the ancestor among its siblings. You build this path similar to the way you compute the lvl column. That is, start with an empty binary string for the root node in the anchor query. Then, in the recursive query you concatenate the parent’s path with the node’s sort position among siblings after you convert it to a binary segment. You use the ROW_NUMBER function to compute the position, partitioned by the parent (mgrid in our case) and ordered by the relevant ordering column (empid in our case). You convert the row number to a binary value of a sufficient size depending on the maximum number of direct children that a parent can have in your graph. BINARY(1) supports up to 255 children per parent, BINARY(2) supports 65,535, BINARY(3): 16,777,215, BINARY(4): 4,294,967,295. In a recursive CTE, corresponding columns in the anchor and recursive queries must be of the same type and size, so make sure to convert the sort path to a binary value of the same size in both.
Here’s the code implementing Step 1 in our solution (assuming BINARY(1) is sufficient per segment meaning that you have no more than 255 direct subordinates per manager):
DECLARE @root AS INT = 1;
WITH C AS
(
SELECT empid, mgrid, empname,
CAST(0x AS VARBINARY(900)) AS sortpath
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname,
CAST(M.sortpath
+ CAST(ROW_NUMBER() OVER(PARTITION BY S.mgrid ORDER BY S.empid)
AS BINARY(1))
AS VARBINARY(900)) AS sortpath
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
)
SELECT empid, mgrid, empname, sortpath
FROM C;
This code generates the following output:
empid mgrid empname sortpath
------ ------ -------- -----------
1 NULL David 0x
2 1 Eitan 0x01
3 1 Ina 0x02
7 3 Aaron 0x0201
9 7 Rita 0x020101
11 7 Gabriel 0x020102
12 9 Emilia 0x02010101
13 9 Michael 0x02010102
14 9 Didi 0x02010103
4 2 Seraph 0x0101
5 2 Jiru 0x0102
6 2 Steve 0x0103
8 5 Lilach 0x010201
10 5 Sean 0x010202
Note that I used an empty binary string as the sort path for the root node of the single subtree that we are querying here. In case the anchor member can potentially return multiple subtree roots, simply start with a segment that is based on a ROW_NUMBER computation in the anchor query, similar to the way you compute it in the recursive query. In such a case, your sort path will be one segment longer.
What’s left to do in Step 2, is to create the desired result seqdepth column by computing row numbers that are ordered by sortpath in the outer query, like so
DECLARE @root AS INT = 1;
WITH C AS
(
SELECT empid, mgrid, empname,
CAST(0x AS VARBINARY(900)) AS sortpath
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname,
CAST(M.sortpath
+ CAST(ROW_NUMBER() OVER(PARTITION BY S.mgrid ORDER BY S.empid)
AS BINARY(1))
AS VARBINARY(900)) AS sortpath
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
)
SELECT empid, mgrid, empname,
ROW_NUMBER() OVER(ORDER BY sortpath) AS seqdepth
FROM C
ORDER BY seqdepth;
This solution is the logical equivalent of using the standard SEARCH DEPTH FIRST option shown earlier along with its desired output.
Once you have a sequence column reflecting depth first search order (seqdepth in our case), with just a little bit more effort you can generate a very nice visual depiction of the hierarchy. You will also need the aforementioned lvl column. You order the outer query by the sequence column. You return some attribute that you want to use to represent the node (say, empname in our case), prefixed by some string (say ' | ') replicated lvl times. Here’s the complete code to achieve such visual depiction:
DECLARE @root AS INT = 1;
WITH C AS
(
SELECT empid, empname, 0 AS lvl,
CAST(0x AS VARBINARY(900)) AS sortpath
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.empname, M.lvl + 1 AS lvl,
CAST(M.sortpath
+ CAST(ROW_NUMBER() OVER(PARTITION BY S.mgrid ORDER BY S.empid)
AS BINARY(1))
AS VARBINARY(900)) AS sortpath
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
)
SELECT empid,
ROW_NUMBER() OVER(ORDER BY sortpath) AS seqdepth,
REPLICATE(' | ', lvl) + empname AS emp
FROM C
ORDER BY seqdepth;
This code generates the following output:
empid seqdepth emp ------ --------- -------------------- 1 1 David 2 2 | Eitan 4 3 | | Seraph 5 4 | | Jiru 8 5 | | | Lilach 10 6 | | | Sean 6 7 | | Steve 3 8 | Ina 7 9 | | Aaron 9 10 | | | Rita 12 11 | | | | Emilia 13 12 | | | | Michael 14 13 | | | | Didi 11 14 | | | Gabriel
That’s pretty cool!
CYCLE clause
Graph structures may have cycles. Those cycles could be valid or invalid. An example for valid cycles is a graph representing highways and roads connecting cities and towns. That’s what’s referred to as a cyclic graph. Conversely, a graph representing an employee hierarchy such as in our case is not supposed to have cycles. That’s what’s referred to as an acyclic graph. However, suppose that due to some erroneous update, you end up with a cycle unintentionally. For example, suppose that by mistake you update the manager ID of the CEO (employee 1) to employee 14 by running the following code:
UPDATE Employees
SET mgrid = 14
WHERE empid = 1;
You now have an invalid cycle in the employee hierarchy.
Whether cycles are valid or invalid, when you traverse the graph structure, you certainly don’t want to keep pursuing a cyclic path repeatedly. In both cases you want to stop pursuing a path once a nonfirst occurrence of the same node is found, and mark such a path as cyclic.
So what happens when you query a graph that has cycles using a recursive query, with no mechanism in place to detect those? This depends on the implementation. In SQL Server, at some point you’ll hit the max recursion limit, and your query will be aborted. For example, assuming you ran the above update that introduced the cycle, try running the following recursive query to identify the subtree of employee 1:
DECLARE @root AS INT = 1;
WITH C AS
(
SELECT empid, mgrid, empname
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
)
SELECT empid, mgrid, empname
FROM C;
Since this code doesn’t set an explicit max recursion limit, the default limit of 100 is assumed. SQL Server aborts the execution of this code before completion and generates an error:
empid mgrid empname ------ ------ -------- 1 14 David 2 1 Eitan 3 1 Ina 7 3 Aaron 9 7 Rita 11 7 Gabriel 12 9 Emilia 13 9 Michael 14 9 Didi 1 14 David 2 1 Eitan 3 1 Ina 7 3 Aaron ...
The statement terminated. The maximum recursion 100 has been exhausted before statement completion.
The SQL standard defines a clause called CYCLE for recursive CTEs, enabling you to deal with cycles in your graph. You specify this clause right before the outer query. If a SEARCH clause is also present, you specify it first and then the CYCLE clause. Here’s the syntax of the CYCLE clause:
SET <cycle mark column> TO <cycle mark value> DEFAULT <non-cycle mark value>
USING <path column>
The detection of a cycle is based on the specified cycle column list. For example, in our employee hierarchy, you would probably want to use the empid column for this purpose. When the same empid value appears for the second time, a cycle is detected, and the query does not pursue such a path any further. You specify a new cycle mark column that will indicate whether a cycle was found or not, and your own values as the cycle mark and non-cycle mark values. For example, those could be 1 and 0 or 'Yes' and 'No', or any other values of your choosing. In the USING clause you specify a new array column name that will hold the path of nodes found thus far.
Here’s how you would handle a request for subordinates of some input root employee, with the ability to detect cycles based on the empid column, indicating 1 in the cycle mark column when a cycle is detected, and 0 otherwise:
DECLARE @root AS INT = 1;
WITH C AS
(
SELECT empid, mgrid, empname
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
)
CYCLE empid SET cycle TO 1 DEFAULT 0
------------------------------------
SELECT empid, mgrid, empname
FROM C;
Here’s the desired output of this code:
empid mgrid empname cycle ------ ------ -------- ------ 1 14 David 0 2 1 Eitan 0 3 1 Ina 0 7 3 Aaron 0 9 7 Rita 0 11 7 Gabriel 0 12 9 Emilia 0 13 9 Michael 0 14 9 Didi 0 1 14 David 1 4 2 Seraph 0 5 2 Jiru 0 6 2 Steve 0 8 5 Lilach 0 10 5 Sean 0
T-SQL currently doesn’t support the CYCLE clause, but there is a workaround that provides a logical equivalent. It involves three steps. Recall that earlier you built a binary sort path to handle the recursive search order. In a similar way, as the first step in the solution, you build a character string-based ancestors path made of the node IDs (employee IDs in our case) of the ancestors leading to the current node, including the current node. You want separators between the node IDs, including one at the beginning and one at the end.
Here’s the code to build such an ancestors path:
DECLARE @root AS INT = 1;
WITH C AS
(
SELECT empid, mgrid, empname,
CAST('.' + CAST(empid AS VARCHAR(4)) + '.' AS VARCHAR(900)) AS ancpath
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname,
CAST(M.ancpath + CAST(S.empid AS VARCHAR(4)) + '.' AS VARCHAR(900)) AS ancpath
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
)
SELECT empid, mgrid, empname, ancpath
FROM C;
This code generates the following output, still pursuing cyclic paths, and therefore aborting before completion once the max recursion limit is exceeded:
empid mgrid empname ancpath ------ ------ -------- ------------------- 1 14 David .1. 2 1 Eitan .1.2. 3 1 Ina .1.3. 7 3 Aaron .1.3.7. 9 7 Rita .1.3.7.9. 11 7 Gabriel .1.3.7.11. 12 9 Emilia .1.3.7.9.12. 13 9 Michael .1.3.7.9.13. 14 9 Didi .1.3.7.9.14. 1 14 David .1.3.7.9.14.1. 2 1 Eitan .1.3.7.9.14.1.2. 3 1 Ina .1.3.7.9.14.1.3. 7 3 Aaron .1.3.7.9.14.1.3.7. ...
The statement terminated. The maximum recursion 100 has been exhausted before statement completion.
Eyeballing the output, you can identify a cyclic path when the current node appears in the path for the nonfirst time, such as in the path '.1.3.7.9.14.1.'.
In the second step of the solution you produce the cycle mark column. In the anchor query you simply set it to 0 since clearly a cycle cannot be found in the first node. In the recursive member you use a CASE expression that checks with a LIKE-based predicate whether the current node ID already appears in the parent’s path, in which case it returns the value 1, or not, in which case it returns the value 0.
Here’s the code implementing Step 2:
DECLARE @root AS INT = 1;
WITH C AS
(
SELECT empid, mgrid, empname,
CAST('.' + CAST(empid AS VARCHAR(4)) + '.' AS VARCHAR(900)) AS ancpath,
0 AS cycle
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname,
CAST(M.ancpath + CAST(S.empid AS VARCHAR(4)) + '.' AS VARCHAR(900)) AS ancpath,
CASE WHEN M.ancpath LIKE '%.' + CAST(S.empid AS VARCHAR(4)) + '.%' THEN 1
ELSE 0 END AS cycle
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
)
SELECT empid, mgrid, empname, ancpath, cycle
FROM C;
This code generates the following output, again, still pursuing cyclic paths and failing once the max recursion limit is reached:
empid mgrid empname ancpath cycle ------ ------ -------- ------------------- ------ 1 14 David .1. 0 2 1 Eitan .1.2. 0 3 1 Ina .1.3. 0 7 3 Aaron .1.3.7. 0 9 7 Rita .1.3.7.9. 0 11 7 Gabriel .1.3.7.11. 0 12 9 Emilia .1.3.7.9.12. 0 13 9 Michael .1.3.7.9.13. 0 14 9 Didi .1.3.7.9.14. 0 1 14 David .1.3.7.9.14.1. 1 2 1 Eitan .1.3.7.9.14.1.2. 0 3 1 Ina .1.3.7.9.14.1.3. 1 7 3 Aaron .1.3.7.9.14.1.3.7. 1 ...
The statement terminated. The maximum recursion 100 has been exhausted before statement completion.
The third and last step is to add a predicate to the ON clause of the recursive member that pursues a path only if a cycle was not detected in the parent’s path.
Here’s the code implementing Step 3, which is also the complete solution:
DECLARE @root AS INT = 1;
WITH C AS
(
SELECT empid, mgrid, empname,
CAST('.' + CAST(empid AS VARCHAR(4)) + '.' AS VARCHAR(900)) AS ancpath,
0 AS cycle
FROM dbo.Employees
WHERE empid = @root
UNION ALL
SELECT S.empid, S.mgrid, S.empname,
CAST(M.ancpath + CAST(S.empid AS VARCHAR(4)) + '.' AS VARCHAR(900)) AS ancpath,
CASE WHEN M.ancpath LIKE '%.' + CAST(S.empid AS VARCHAR(4)) + '.%' THEN 1
ELSE 0 END AS cycle
FROM C AS M
INNER JOIN dbo.Employees AS S
ON S.mgrid = M.empid
AND M.cycle = 0
)
SELECT empid, mgrid, empname, cycle
FROM C;
This code runs to completion, and generates the following output:
empid mgrid empname cycle ------ ------ -------- ----------- 1 14 David 0 2 1 Eitan 0 3 1 Ina 0 7 3 Aaron 0 9 7 Rita 0 11 7 Gabriel 0 12 9 Emilia 0 13 9 Michael 0 14 9 Didi 0 1 14 David 1 4 2 Seraph 0 5 2 Jiru 0 6 2 Steve 0 8 5 Lilach 0 10 5 Sean 0
You identify the erroneous data easily here, and fix the problem by setting the manager ID of the CEO to NULL, like so:
UPDATE Employees
SET mgrid = NULL
WHERE empid = 1;
Run the recursive query and you will find that there are no cycles present.
Conclusion
Recursive CTEs enable you to write concise declarative solutions for purposes such as traversing graph structures. A recursive CTE has at least one anchor member, which gets executed once, and at least one recursive member, which gets executed repeatedly until it returns an empty result set. Using a query option called MAXRECURSION you can control the maximum number of allowed executions of the recursive member as a safety measure. To limit the executions of the recursive member programmatically for filtering purposes you can maintain a column that tracks the level of the current node with respect to the root node.
The SQL standard supports two very powerful options for recursive CTEs that are currently not available in T-SQL. One is a clause called SEARCH that controls the recursive search order, and another is a clause called CYCLE that detects cycles in the traversed paths. I provided logically equivalent solutions that are currently available in T-SQL. If you find that the unavailable standard features could be important future additions to T-SQL, make sure to vote for them here:
- Add support for ISO/IEC SQL SEARCH clause to recursive CTEs in T-SQL
- Add support for ISO/IEC SQL CYCLE clause to recursive CTEs in T-SQL
This article concludes the coverage of the logical aspects of CTEs. Next month I’ll turn my attention to physical/performance considerations of CTEs.
