IGNORE_DUP_KEY slower on clustered indexes

The IGNORE_DUP_KEY option for unique indexes specifies how SQL Server responds to an attempt to INSERT duplicate values: It only applies to tables (not views) and only to inserts. Any insert portion of a MERGE statement ignores any IGNORE_DUP_KEY index setting.

When IGNORE_DUP_KEY is OFF, the first duplicate encountered results in an error, and none of the new rows are inserted.

When IGNORE_DUP_KEY is ON, inserted rows that would violate uniqueness are discarded. The remaining rows are successfully inserted. A warning message is emitted instead of an error:

Article Summary

The IGNORE_DUP_KEY index option can be specified for both clustered and nonclustered unique indexes. Using it on a clustered index can result in much poorer performance than for a nonclustered unique index.

The size of the performance difference depends on how many uniqueness violations are encountered during the INSERT operation. The more violations, the worse the clustered unique index performs by comparison. If there are no violations at all, the clustered index insert may even perform better.

Clustered unique index inserts

For a clustered unique index with IGNORE_DUP_KEY set, duplicates are handled by the storage engine.

Much of the work involved in inserting each row is performed before the duplicate is detected. For example, a Clustered Index Insert operator navigates down the clustered index b-tree to the point where the new row would go, taking page latches and the usual hierarchy of locks, before it discovers the duplicate key.

When the duplicate key condition is detected, an error is raised. Instead of cancelling execution and returning the error to the client, the error is handled internally. The problematic row is not inserted, and execution continues, looking for the next row to insert. If that row encounters a duplicate key, another error is raised and handled, and so on.

Exceptions are very expensive to throw and catch. A significant number of duplicates will slow down execution very noticeably.

Nonclustered unique index inserts

For a nonclustered unique index with IGNORE_DUP_KEY set, duplicates are handled by the query processor. Duplicates are detected, and a warning emitted, before each insert is attempted.

The query processor removes duplicates from the insert stream, ensuring that no duplicates are seen by the storage engine. As a result, no unique key violation errors are raised or handled internally.

The trade-off

There is a trade-off between the cost of detecting and removing duplicate keys in the execution plan, versus the cost of performing significant insert-related work, and throwing and catching errors when a duplicate is found.

If duplicates are expected to be very rare, the storage engine solution (clustered index) may well be more efficient. When duplicates are less rare, the query processor approach will likely pay dividends. The exact crossover point will depend on factors such as the runtime efficiency of the execution plan components used to detect and remove duplicates.

The remainder of this article provides a demo and looks in more detail at why the storage engine approach can perform so poorly.

Demo

The following script creates a temporary table with a million rows. It has 1,000 unique values and 1,000 rows for each unique value. This data set will be used as the data source for inserts into tables with different index configurations.

DROP TABLE IF EXISTS #Data;
GO
CREATE TABLE #Data (c1 integer NOT NULL);
GO
SET NOCOUNT ON;
SET STATISTICS XML OFF;

DECLARE
    @Loop integer = 1,
    @N integer = 1;

WHILE @N <= 1000
BEGIN
    SET @Loop = 1;

    BEGIN TRANSACTION;

        -- Add 1,000 copies of the current loop value
        WHILE @Loop <= 50
        BEGIN
            INSERT #Data 
                (c1) 
            VALUES 
                (@N), (@N), (@N), (@N), (@N),
                (@N), (@N), (@N), (@N), (@N),
                (@N), (@N), (@N), (@N), (@N),
                (@N), (@N), (@N), (@N), (@N);

            SET @Loop += 1;
        END;

    COMMIT TRANSACTION;

    SET @N += 1;
END;

CREATE CLUSTERED INDEX cx 
ON #Data (c1) 
WITH (MAXDOP = 1);

Baseline

The following insert into a table variable with a non-unique clustered index takes around 900ms:

DECLARE @T table 
(
    c1 integer NOT NULL
        INDEX cuq CLUSTERED (c1)
);

INSERT @T 
    (c1) 
SELECT 
    D.c1 
FROM #Data AS D;

Note the lack of IGNORE_DUP_KEY on the target table variable.

Clustered unique index

Inserting the same data to a unique clustered index with IGNORE_DUP_KEY set ON takes around 15,900ms — almost 18 times worse:

DECLARE @T table 
(
    c1 integer NOT NULL
        UNIQUE CLUSTERED 
        WITH (IGNORE_DUP_KEY = ON)
);

INSERT @T 
    (c1) 
SELECT 
    D.c1 
FROM #Data AS D;

Nonclustered unique index

Inserting the data to a unique nonclustered index with IGNORE_DUP_KEY set ON takes around 700ms:

DECLARE @T table 
(
    c1 integer NOT NULL
        UNIQUE NONCLUSTERED
        WITH (IGNORE_DUP_KEY = ON)
);

INSERT @T 
    (c1) 
SELECT 
    D.c1 
FROM #Data AS D;

Performance summary

The baseline test takes 900ms to insert all one million rows. The nonclustered index test takes 700ms to insert just the 1,000 distinct keys. The clustered index test takes 15,900ms to insert the same 1,000 unique rows.

This test is deliberately set up to highlight poor performance of the storage engine implementation, by generating 999 units of wasted work (latches, locks, error handling) for each successful row.

The intended message is not that IGNORE_DUP_KEY will always perform poorly on clustered indexes, just that it might, and there can be a big difference between clustered and nonclustered indexes.

Clustered Index Execution Plan

There is not a huge amount to see in the clustered index insert plan:

There are 1,000,000 rows being passed to the Clustered Index Insert operator, which is shown as ‘returning’ 1,000 rows. Digging into the plan details, we can see:

• 1,244,008 logical reads at the insert operator.
• The vast bulk of execution time is spent at the Insert operator.
• 11ms of SOS_SCHEDULER_YIELD waits (i.e. no other waits).

Nothing that really explains the 15,900 ms of elapsed time.

Why performance is so poor

It is apparent that this plan will have to do a lot of work for each row:

• Navigate the clustered index b-tree levels, latching and locking as it goes, to find the insertion point for the new record.
• If any of the index pages needed are not in memory, they will need to be fetched from disk.
• Construct a new b-tree row in memory.
• Prepare log records.
• If an key duplicate is found (that is not a ghost record), raise an error, handle that error internally, release the current row, and resume at a suitable point in the code to process the next candidate row.

That is all a fair amount of work, and remember it all happens for each row.

The part that I want to concentrate on is the error raising and handling, because it is extremely expensive. The remaining aspects noted above were already made as cheap as possible by using a table variable and temporary table in the demo.

Exceptions

The first thing I want to do is show that the Clustered Index Insert operator really does raise an exception when it encounters a duplicate key.

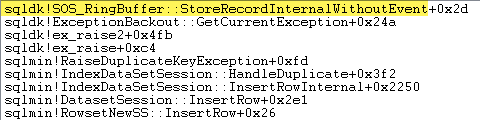
One way to show this directly is by attaching a debugger and capturing a stack trace at the point the exception is thrown:

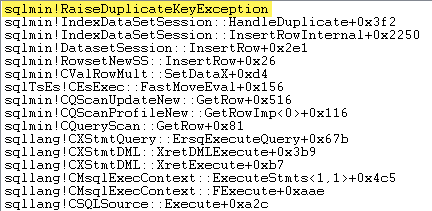
The important point here is that throwing and catching exceptions is very expensive.

Monitoring SQL Server using Windows Performance Recorder while the test was running, and analyzing the results in Windows Performance Analyzer shows:

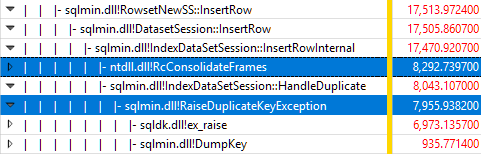
Almost all the query execution time is spent in sqlmin!IndexDataSetSession::InsertRowInternal as would be expected for a query that does little else except insert rows.

The surprise is that 45% of that time is spent raising exceptions via sqlmin!RaiseDuplicateKeyException and another 47% is spent in the associated exception catch block (the ntdll!RcConsolidateFrames hierarchy) .

To summarise: Raising and catching exceptions makes up 92% of the execution time of our test clustered index insert query.

Data collection issues

Sharp-eyed readers may notice a significant amount – about 12% – of exception raising time spent in sqlmin!DumpKey in the Windows Performance Analyzer graphic. This is worth exploring quickly, along with a couple of related items.

As part of raising an exception, SQL Server has to collect some data that is only available at the time the error occurred. The error number associated with a duplicate key exception is 2627. The message text in sys.messages for that error number is:

Information to populate those place markers needs to be gathered at the time the error is raised — it will not be available later! That means looking up and formatting the type of constraint, its name, the full name of the target object, and the specific key value. All that takes time.

The following stack trace shows the server formatting the duplicate key value as a Unicode string during the DumpKey call:

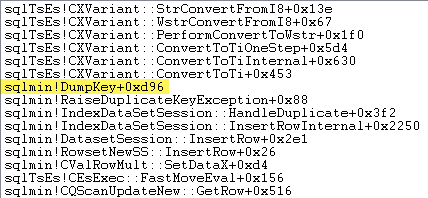
Exception handling also involves capturing a stack trace:

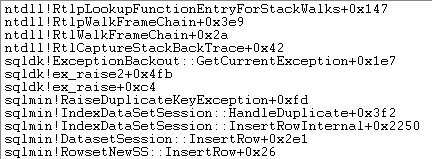
SQL Server also records information about exceptions (including stack frames) in a small ring buffer, as the following shows:

You can see those ring buffer entries using a command like:

SELECT TOP (10)
    date_time = 
        DATEADD
        (
            MILLISECOND, 
            DORB.[timestamp] - DOSI.ms_ticks, 
            SYSDATETIME()
        ),
    record = CONVERT(xml, DORB.record)
FROM sys.dm_os_ring_buffers AS DORB
CROSS JOIN sys.dm_os_sys_info AS DOSI
WHERE 
    DORB.ring_buffer_type = N'RING_BUFFER_EXCEPTION'
ORDER BY 
    DORB.[timestamp] DESC;

An example of the xml record for a duplicate key exception follows. Note the stack frames:

  
    
    2627
    14
    1
    0
    0
  
  
    0X00007FFAC659E80A
    0X00007FFACBAC0EFD
    0X00007FFACBAA1252
    0X00007FFACBA9E040
    0X00007FFACAB55D53
    0X00007FFACAB55C06
    0X00007FFACB3E3D0B
    0X00007FFAC92020EC
    0X00007FFACAB5B2FA
    0X00007FFACABA3B9B
    0X00007FFACAB3D89F
    0X00007FFAC6A9D108
    0X00007FFAC6AB2BBF
    0X00007FFAC6AB296F
    0X00007FFAC6A9B7D0
    0X00007FFAC6A9B233
  

All this background work happens for every exception. In our test, that means it happens 999,000 times — once for every row that encounters a duplicate key violation.

There are many ways to see of this, for example by running a Profiler trace using the Exception event in the Errors and Warnings class. In our test case, this will eventually produce 999,000 rows with TextData elements like this:

Attaching Profiler means that each exception handling event acquires a great deal of additional overhead, as the extra data needed is collected and formatted. The default data mentioned previously is always collected, even if no one is actively consuming the information.

To be clear: The performance numbers reported in this article were all obtained without a debugger attached, and no other monitoring active.

Nonclustered Index Execution Plan

Despite being so much quicker, the nonclustered index insert plan is quite a bit more complex, so I will break it into two parts.

The general theme is that this plan is faster because it eliminates duplicates before trying to insert them into the target table.

Part 1

First, the right-hand side of the nonclustered index plan:

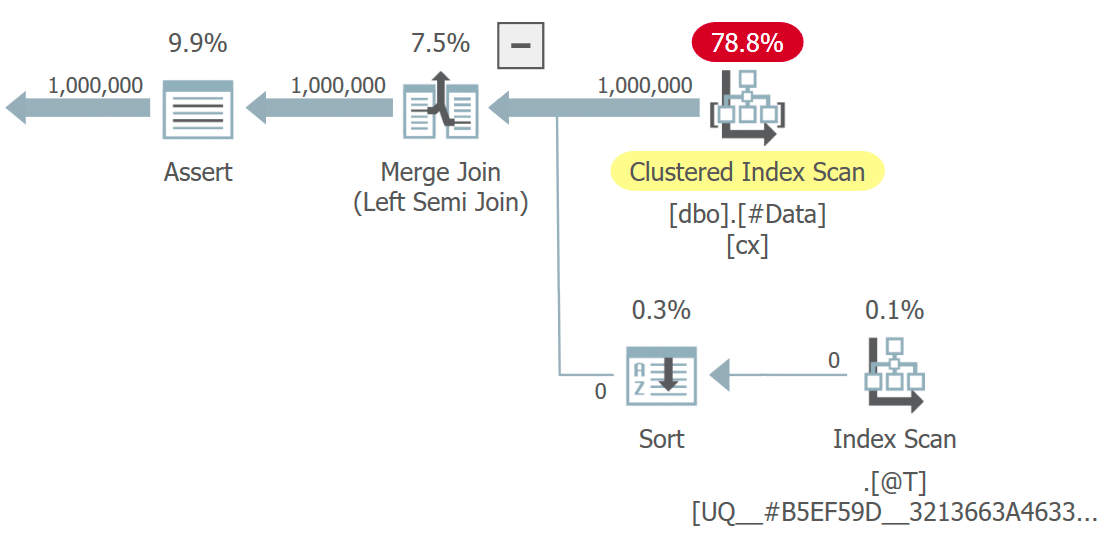
This part of the plan rejects any rows that have a key match in the target table for the unique index with IGNORE_DUP_KEY set ON.

You might be expecting to see an Anti Semi Join here, but SQL Server does not have the necessary infrastructure to emit the required duplicate key warning with an Anti Semi Join operator. (If that does not already make sense, it should shortly.)

Instead, we get a plan with a number of interesting features:

• The Clustered Index Scan is Ordered:True to provide input to the Merge Left Semi Join sorted by column c1 in the #Data table.
• The Index Scan of the table variable is Ordered:False
• The Sort orders rows by column c1 in the table variable. This order could have been provided by an ordered scan of the table variable index on c1, but the optimizer decides the Sort is the cheapest way to provide the required level of Halloween Protection.
• The table variable Index Scan has internal UPDLOCK and SERIALIZABLE hints applied to ensure target stability during plan execution.
• The Merge Left Semi Join checks for matches in the table variable for each value of c1 returned from the #Data table. Unlike a regular semi join, it emits every row received on its upper input. It sets a flag in a probe column to indicate if the current row found a match or not. The probe column is emitted from the Merge Left Semi Join as an expression named Expr1012.
• The Assert operator checks the value of the probe column Expr1012. The first time it sees a row with a non-null probe column value (indicating that an index key match was found), it emits a “Duplicate key was ignored” message.
• The Assert only passes on rows where the probe column is null. This eliminates incoming rows that would produce a duplicate key error.

That all might seem complex, but it is essentially as simple as setting a flag if a match is found, emitting a warning the first time the flag is set, and only passing rows on toward the insert that do not already exist in the target table.

Part 2

The second part of the plan follows the Assert operator:

The previous part of the plan removed rows that had a match in the target table. This part of the plan removes duplicates within the insert set.

For example, imagine there are no rows in the target table where c1 = 1. We might still cause a duplicate key error if we try to insert two rows with c1 = 1 from the source table. We need to avoid that to honour the semantics of IGNORE_DUP_KEY = ON.

This aspect is handled by the Segment and Top operators.

The Segment operator sets a new flag (labelled Segment1015) when it encounters a row with a new value for c1. Since rows are presented in c1 order (thanks to the order-preserving Merge), the plan can rely on all rows with the same c1 value arriving in a contiguous stream.

The Top operator passes on one row for each group of duplicates, as indicated by the Segment flag. If the Top operator encounters more than one row for the same Segment group (c1 value), it emits a “Duplicate key was ignored” warning, if that is the first time the plan has encountered that condition.

The net effect of all this is that only one row is passed to the insert operators for each unique value of c1, and a warning is generated if needed.

The execution plan has now eliminated all potential duplicate key violations, so the remaining Table Insert and Index Insert operators can safely insert rows to the heap and nonclustered index without fear of a duplicate key error.

Remember that the UPDLOCK and SERIALIZABLE hints applied to the target table ensure that set cannot change during execution. In other words, a concurrent statement cannot change target table such that a duplicate key error would occur at the Insert operators. That is not a concern here since we are using a private table variable, but SQL Server still adds the hints as a general safety measure.

Without those hints, a concurrent process could add a row to the target table that would generate a duplicate key violation, despite the checks made by part 1 of the plan. SQL Server needs to be sure that the existence check results remain valid.

The curious reader can see some of the features described above by enabling trace flags 3604 and 8607 to see the optimizer output tree:

PhyOp_RestrRemap
    PhyOp_StreamUpdate(INS TBL: @T, iid 0x2 as IDX, Sort(QCOL: .c1, )), {
            - COL: Bmk10001013 = COL: Bmk1000 
            - COL: c11014 = QCOL: .c1} 
        PhyOp_StreamUpdate(INS TBL: @T, iid 0x0 as TBLInsLocator(COL: Bmk1000  ) REPORT-COUNT), {
                - QCOL: .c1= QCOL: [D].c1} 
            PhyOp_GbTop Group(QCOL: [D].c1,) WARN-DUP
                PhyOp_StreamCheck (WarnIgnoreDuplicate TABLE) 
                    PhyOp_MergeJoin x_jtLeftSemi M-M, Probe COL: Expr1012  ( QCOL: [D].c1) = ( QCOL: .c1)
                        PhyOp_Range TBL: #Data(alias TBL: D)(1) ASC
                        PhyOp_Sort +s -d QCOL: .c1
                            PhyOp_Range TBL: @T(2) ASC Hints( UPDLOCK SERIALIZABLE FORCEDINDEX )
                        ScaOp_Comp x_cmpIs
                            ScaOp_Identifier QCOL: [D].c1
                            ScaOp_Identifier QCOL: .c1
                    ScaOp_Logical x_lopIsNotNull
                        ScaOp_Identifier COL: Expr1012 

Final Thoughts

The IGNORE_DUP_KEY index option is not something most people will use very often. Still, it is interesting to look at how this functionality is implemented, and why there can be large performance differences between IGNORE_DUP_KEY on clustered and nonclustered indexes.

In many cases, it will pay to follow the lead of the query processor and look to write queries that eliminate duplicates explicitly, rather than relying on IGNORE_DUP_KEY. In our example, that would mean writing:

DECLARE @T table 
(
    c1 integer NOT NULL
        UNIQUE CLUSTERED -- no IGNORE_DUP_KEY!
);

INSERT @T 
    (c1) 
SELECT DISTINCT -- Remove duplicates
    D.c1 
FROM #Data AS D;

This executes in around 400ms, just for the record.

Update

In SQL Server 2017 onward, it is possible to specify the (SUPPRESS_MESSAGES = ON) option after IGNORE_DUP_KEY = ON. In that case, the optimizer will always produce the faster nonclustered-style plan, even for a clustered index. Message suppression only works with that plan shape.