SQL Server 2016 : Performance Impact of Always Encrypted

As part of T-SQL Tuesday #69, I've blogged about the limitations of Always Encrypted, and I mentioned there that performance could be negatively impacted by its use (as you might expect, stronger security often does have trade-offs). In this post, I wanted to take a quick look at this, keeping in mind (again) that these results are based off of CTP 2.2 code, so very early in the development cycle, and are not necessarily reflective of the performance you'll see come RTM.

First, I wanted to demonstrate that Always Encrypted works from client applications even if the latest version of SQL Server 2016 is not installed there. You do, though, have to install the .NET Framework 4.6 preview (most recent version here, and that may change) in order to support the Column Encryption Setting connection string attribute. If you are running Windows 10, or have installed Visual Studio 2015, this step is not necessary, as you should already have a recent enough version of the .NET Framework.

Next, you need to make sure the Always Encrypted certificate exists on all clients. You create the master and column encryption keys within the database, as any Always Encrypted tutorial will show you, then you need to export the certificate from that machine, and import it on the others where application code will run. Open certmgr.msc, and expand Certificates – Current User > Personal > Certificates, and there should be one there called Always Encrypted Certificate. Right-click that, choose All Tasks > Export, and follow the prompts. I exported the private key and provided a password, which produced a .pfx file. Then you just repeat the opposite process on the client machines: Open certmgr.msc, expand Certificates – Current User > Personal, right-click Certificates, choose All Tasks > Import, and point it at the .pfx file you created above. (Official help here.)

(There are more secure ways to manage these certificates – it is not likely you'd just want to deploy the certificate like this to all machines, as you will soon ask yourself what was the point? I was only doing this in my isolated environment for the purposes of this demo – I wanted to make sure my application was retrieving data over the wire and not just in local memory.)

We create two databases, one with an encrypted table, and one without. We do this to isolate connection strings and also to measure space usage. Of course, there are more granular ways to control which commands need to use an encryption-enabled connection – see the note titled "Controlling the performance impact…" in this article.

The tables look like this:

-- encrypted copy, in database Encrypted

CREATE TABLE dbo.Employees
(
  ID INT IDENTITY(1,1) PRIMARY KEY,
  LastName NVARCHAR(32) COLLATE Latin1_General_BIN2 
    ENCRYPTED WITH (ENCRYPTION_TYPE = DETERMINISTIC,
	ALGORITHM = 'AEAD_AES_256_CBC_HMAC_SHA_256',
	COLUMN_ENCRYPTION_KEY = ColumnKey) NOT NULL,
  Salary INT
    ENCRYPTED WITH (ENCRYPTION_TYPE = RANDOMIZED,
	ALGORITHM = 'AEAD_AES_256_CBC_HMAC_SHA_256',
	COLUMN_ENCRYPTION_KEY = ColumnKey) NOT NULL
);

-- unencrypted copy, in database Normal

CREATE TABLE dbo.Employees
(
  ID INT IDENTITY(1,1) PRIMARY KEY,
  LastName NVARCHAR(32) COLLATE Latin1_General_BIN2 NOT NULL,
  Salary INT NOT NULL
);

With these tables in place, I wanted to set up a very simple command-line application to perform the following tasks against both the encrypted and unencrypted versions of the table:

• Insert 100,000 employees, one at a time
• Read through 100 random rows, 1,000 times
• Output timestamps before and after each step

So we have a stored procedure in a completely separate database used to produce random integers to represent salaries, and random Unicode strings of varying lengths. We're going to do this one at a time to better simulate real usage of 100,000 inserts happening independently (though not concurrently, as I am not brave enough to try to properly develop and manage a multi-threaded C# application, or try to coordinate and synchronize multiple instances of a single application).

CREATE DATABASE Utility;
GO

USE Utility;
GO

CREATE PROCEDURE dbo.GenerateNameAndSalary
  @Name NVARCHAR(32) OUTPUT,
  @Salary INT OUTPUT
AS
BEGIN
  SET NOCOUNT ON;
  SELECT @Name = LEFT(CONVERT(NVARCHAR(32), CRYPT_GEN_RANDOM(64)), RAND() * 32 + 1);
  SELECT @Salary = CONVERT(INT, RAND()*100000)/100*100;
END
GO

A couple of rows of sample output (we don't care about the actual content of the string, just that it varies):

酹２׿ዌ륒㦢㮧羮怰㉤盿⚉嗝䬴敏⽁캘♜鼹䓧
98600

贓峂쌄탠❼缉腱蛽☎뱶
72000

Then the stored procedures the application will ultimately call (these are identical in both databases, since your queries don't need to be changed to support Always Encrypted):

CREATE PROCEDURE dbo.AddPerson
  @LastName NVARCHAR(32),
  @Salary INT
AS
BEGIN
  SET NOCOUNT ON;
  INSERT dbo.Employees(LastName, Salary) SELECT @LastName, @Salary;
END
GO

CREATE PROCEDURE dbo.RetrievePeople
AS
BEGIN
  SET NOCOUNT ON;
  SELECT TOP (100) ID, LastName, Salary 
    FROM dbo.Employees
    ORDER BY NEWID();
END
GO

Now, the C# code, starting with the connectionStrings portion of App.config. The important part being the Column Encryption Setting option for only the database with the encrypted columns (for brevity, assume all three connection strings contain the same Data Source, and the same SQL authentication User ID and Password):

And Program.cs (sorry, for demos like this, I'm terrible at going in and renaming things logically):

using System;
using System.Collections.Generic;
using System.Text;
using System.Configuration;
using System.Data;
using System.Data.SqlClient;

namespace AEDemo
{
    class Program
    {
        static void Main(string[] args)
        {
            using (SqlConnection con1 = new SqlConnection())
            {
                Console.WriteLine(DateTime.UtcNow.ToString("hh:mm:ss.fffffff"));
                string name;
                string EmptyString = "";
                int salary;
                int i = 1;
                while (i <= 100000)
                {
                    con1.ConnectionString = ConfigurationManager.ConnectionStrings["Utility"].ToString();
                    using (SqlCommand cmd1 = new SqlCommand("dbo.GenerateNameAndSalary", con1))
                    {
                        cmd1.CommandType = CommandType.StoredProcedure;
                        SqlParameter n = new SqlParameter("@Name", SqlDbType.NVarChar, 32) 
                                         { Direction = ParameterDirection.Output };
                        SqlParameter s = new SqlParameter("@Salary", SqlDbType.Int) 
                                         { Direction = ParameterDirection.Output };
                        cmd1.Parameters.Add(n);
                        cmd1.Parameters.Add(s);
                        con1.Open();
                        cmd1.ExecuteNonQuery();
                        name = n.Value.ToString();
                        salary = Convert.ToInt32(s.Value);
                        con1.Close();
                    }

                    using (SqlConnection con2 = new SqlConnection())
                    {
                        con2.ConnectionString = ConfigurationManager.ConnectionStrings[args[0]].ToString();
                        using (SqlCommand cmd2 = new SqlCommand("dbo.AddPerson", con2))
                        {
                            cmd2.CommandType = CommandType.StoredProcedure;
                            SqlParameter n = new SqlParameter("@LastName", SqlDbType.NVarChar, 32);
                            SqlParameter s = new SqlParameter("@Salary", SqlDbType.Int);
                            n.Value = name;
                            s.Value = salary;
                            cmd2.Parameters.Add(n);
                            cmd2.Parameters.Add(s);
                            con2.Open();
                            cmd2.ExecuteNonQuery();
                            con2.Close();
                        }
                    }
                    i++;
                }
                Console.WriteLine(DateTime.UtcNow.ToString("hh:mm:ss.fffffff"));
                i = 1;
                while (i <= 1000)
                {
                    using (SqlConnection con3 = new SqlConnection())
                    {
                        con3.ConnectionString = ConfigurationManager.ConnectionStrings[args[0]].ToString();
                        using (SqlCommand cmd3 = new SqlCommand("dbo.RetrievePeople", con3))
                        {
                            cmd3.CommandType = CommandType.StoredProcedure;
                            con3.Open();
                            SqlDataReader rdr = cmd3.ExecuteReader();
                            while (rdr.Read())
                            {
                                EmptyString += rdr[0].ToString();
                            }
                            con3.Close();
                        }
                    }
                    i++;
                }
                Console.WriteLine(DateTime.UtcNow.ToString("hh:mm:ss.fffffff"));
            }
        }
    }
}

Then we can call the .exe with the following command lines:

AEDemoConsole.exe "Normal"
AEDemoConsole.exe "Encrypt"

And it will produce three lines of output for each call: the start time, the time after 100,000 rows were inserted, and the time after 100 rows were read 1,000 times. Here were the results I saw on my system, averaged over 5 runs each:

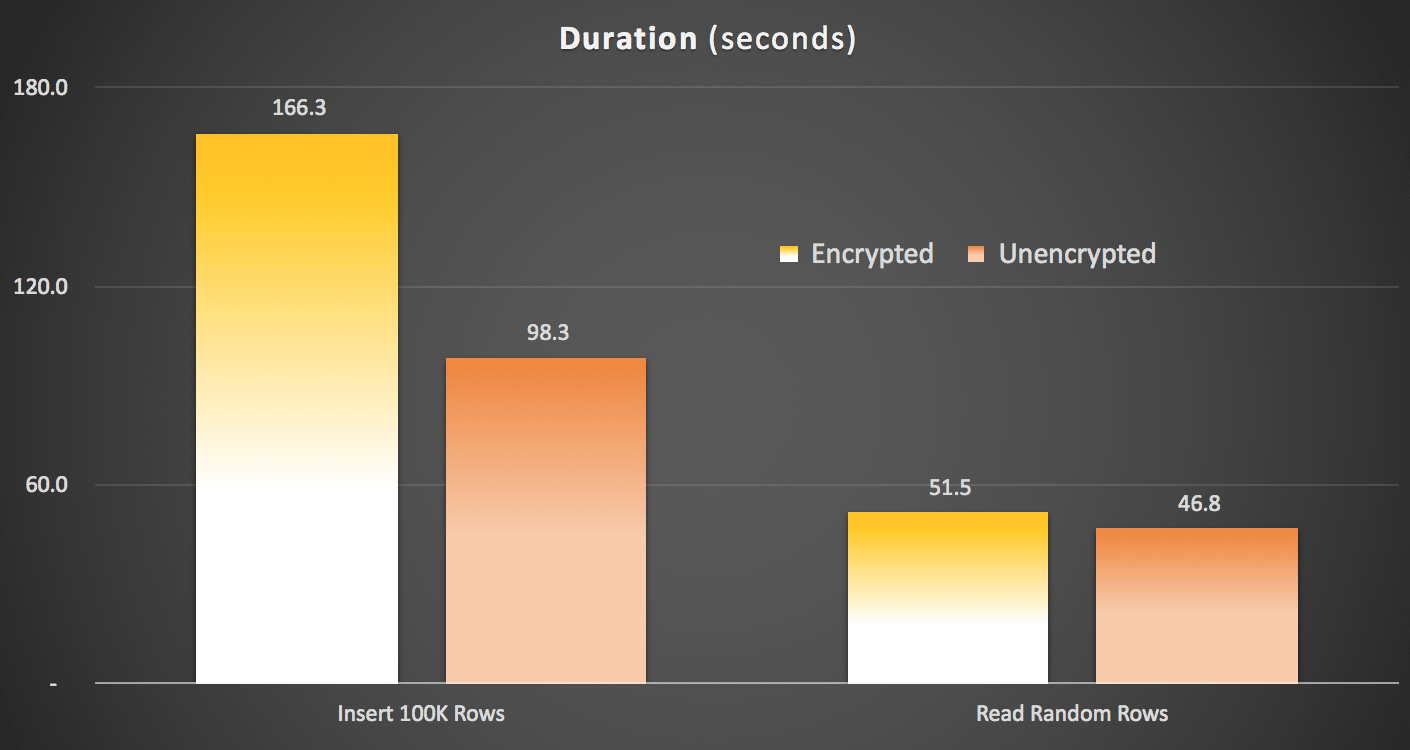Duration (seconds) of writing and reading data

There is a clear impact to writing the data - not quite 2X, but more than 1.5X. There was a much lower delta on reading and decrypting the data - at least in these tests - but that wasn't free, either.

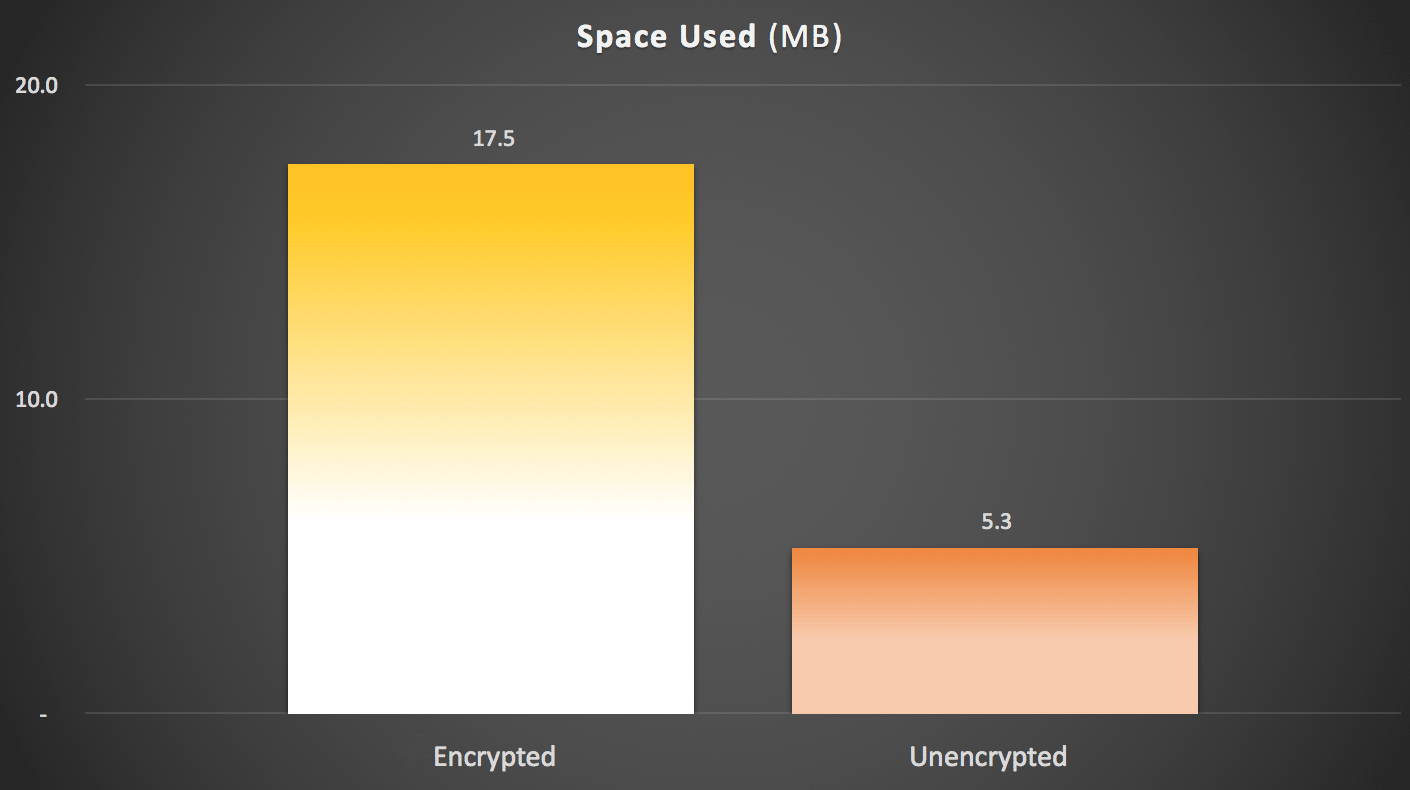
As far as space usage, there is roughly a 3X penalty for storing encrypted data (given the nature of most encryption algorithms, this shouldn't be shocking). Keep in mind this was on a table with only a single clustered primary key. Here were the figures:

Space (MB) used to store data

So obviously there are some penalties with using Always Encrypted, as there typically are with just about all security-related solutions (the saying "no free lunch" comes to mind). I'll repeat that these tests were performed against CTP 2.2, which may be radically different than the final release of SQL Server 2016. Also, these differences I have observed may reflect only the nature of the tests I concocted; obviously I am hoping you can use this approach to test your results against your schema, on your hardware, and with your data access patterns.