Cardinality Estimation for Multiple Predicates

Single Predicates

Estimating the number of rows qualified by a single query predicate is often straightforward. When a predicate makes a simple comparison between a column and a scalar value, the chances are good that the cardinality estimator will be able to derive a good quality estimate from the statistics histogram. For example, the following AdventureWorks query produces an exactly correct estimate of 203 rows (assuming no changes have been made to the data since the statistics were built):

SELECT COUNT_BIG(*)
FROM Production.TransactionHistory AS TH
WHERE TH.TransactionDate = '20070903';

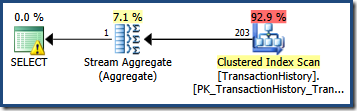
Looking at the statistics histogram for the TransactionDate column, it is clear to see where this estimate came from:

DBCC SHOW_STATISTICS (
    'Production.TransactionHistory', 
    'TransactionDate')
WITH HISTOGRAM;

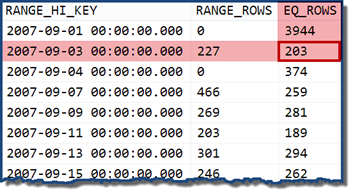
If we change the query to specify a date that falls within a histogram bucket, the cardinality estimator assumes the values are evenly distributed. Using a date of 2007-09-02 produces an estimate of 227 rows (from the RANGE_ROWS entry). As an interesting side-note, the estimate remains at 227 rows regardless of any time portion we might add to the date value (the TransactionDate column is a datetime data type).

If we try the query again with a date of 2007-09-05 or 2007-09-06 (both of which fall between the 2007-09-04 and 2007-09-07 histogram steps), the cardinality estimator assumes the 466 RANGE_ROWS are evenly split between the two values, estimating 233 rows in both cases.

There are many other details to cardinality estimation for simple predicates, but the foregoing will do as a refresher for our present purposes.

The Problems of Multiple Predicates

When a query contains more than one column predicate, cardinality estimation becomes more difficult. Consider the following query with two simple predicates (each of which is easy to estimate alone):

SELECT 
    COUNT_BIG(*)
FROM Production.TransactionHistory AS TH
WHERE
    TH.TransactionID BETWEEN 100000 AND 168412
    AND TH.TransactionDate BETWEEN '20070901' AND '20080313';

The specific ranges of values in the query are deliberately chosen so that both predicates identify exactly the same rows. We could easily modify the query values to result in any amount of overlap, including no overlap at all. Imagine now that you are the cardinality estimator: how would you derive a cardinality estimate for this query?

The problem is harder than it might at first sound. By default, SQL Server automatically creates single-column statistics on both predicate columns. We can also create multi-column statistics manually. Does this give us enough information to produce a good estimate for these specific values? What about the more general case where there might be any degree of overlap?

Using the two single-column statistic objects, we can easily derive an estimate for each predicate using the histogram method described in the previous section. For the specific values in the query above, the histograms show that the TransactionID range is expected to match 68412.4 rows, and the TransactionDate range is expected to match 68,413 rows. (If the histograms were perfect, these two numbers would be exactly the same.)

What the histograms cannot tell us is how many from these two sets of rows will be the same rows. All we can say based on the histogram information is that our estimate should be somewhere between zero (for no overlap at all) and 68412.4 rows (complete overlap).

Creating multi-column statistics provides no assistance for this query (or for range queries in general). Multi-column statistics still only create a histogram over the first named column, essentially duplicating the histogram associated with one of the automatically-created statistics. The additional density information provided by the multi-column statistic can be useful to provide average-case information for queries that contain multiple equality predicates, but they are of no help to us here.

To produce an estimate with a high degree of confidence, we would need SQL Server to provide better information about the data distribution – something like a multi-dimensional statistics histogram. As far as I know, no commercial database engine currently offers a facility like this, though several technical papers have been published on the subject (including a Microsoft Research one that used an internal development of SQL Server 2000).

Without knowing anything about data correlations and overlaps for particular value ranges, it is not clear how we should proceed to produce a good estimate for our query. So, what does SQL Server do here?

SQL Server 7 – 2012

The cardinality estimator in these versions of SQL Server generally assumes that values of different attributes in a table are distributed completely independently of each other. This independency assumption is rarely an accurate refection of the real data, but it does have the advantage of making for simpler calculations.

AND Selectivity

Using the independency assumption, two predicates connected by AND (known as a conjunction) with selectivities S₁ and S₂, result in a combined selectivity of:

(S1 * S2)

In case the term is unfamiliar to you, selectivity is a number between 0 and 1, representing the fraction of rows in the table that pass the predicate. For example, if a predicate selects 12 rows from a table of 100 rows, the selectivity is (12/100) = 0.12.

In our example, the TransactionHistory table contains 113,443 rows in total. The predicate on TransactionID is estimated (from the histogram) to qualify 68,412.4 rows, so the selectivity is (68,412.4 / 113,443) or roughly 0.603055. The predicate on TransactionDate is similarly estimated to have a selectivity of (68,413 / 113,443) = roughly 0.603061.

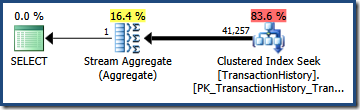
Multiplying the two selectivities (using the formula above) gives a combined selectivity estimate of 0.363679. Multiplying this selectivity by the cardinality of the table (113,443) gives the final estimate of 41,256.8 rows:

OR Selectivity

Two predicates connected by OR (a disjunction) with selectivities S₁ and S₂, results in a combined selectivity of:

(S1 + S2) – (S1 * S2)

The intuition behind the formula is to add the two selectivities, then subtract the estimate for their conjunction (using the previous formula). Clearly we could have two predicates, each of selectivity 0.8, but simply adding them together would produce an impossible combined selectivity of 1.6. Despite the independency assumption, we must recognize that the two predicates may have an overlap, so to avoid double-counting, the estimated selectivity of the conjunction is subtracted.

We can easily modify our running example to use OR:

SELECT COUNT_BIG(*)
FROM Production.TransactionHistory AS TH
WHERE 
    TH.TransactionID BETWEEN 100000 AND 168412
    OR TH.TransactionDate BETWEEN '20070901' AND '20080313';

Substituting the predicate selectivities into the OR formula gives a combined selectivity of:

(0.603055 + 0.603061) - (0.603055 * 0.603061) = 0.842437

Multiplied by the number of rows in the table, this selectivity gives us the final cardinality estimate of 95,568.6:

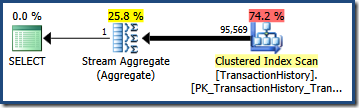
Neither estimate (41,257 for the AND query; 95,569 for the OR query) is particularly good because both are based on a modelling assumption that does not match the data distribution very well. Both queries actually return 68,413 rows (because the predicates identify exactly the same rows).

Trace Flag 4137 – Minimum Selectivity

For SQL Server 2008 (R1) to 2012 inclusive, Microsoft released a fix that changes the way selectivity is computed for the AND case (conjunctive predicates) only. The Knowledge Base article in that link does not contain many details, but it turns out the fix changes the selectivity formula used. Instead of multiplying the individual selectivities, cardinality estimation for conjunctive predicates now uses the lowest selectivity alone.

To activate the changed behaviour, supported trace flag 4137 is required. A separate Knowledge Base article documents that this trace flag is also supported for per-query use via the QUERYTRACEON hint:

SELECT COUNT_BIG(*)
FROM Production.TransactionHistory AS TH
WHERE 
    TH.TransactionID BETWEEN 100000 AND 168412
    AND TH.TransactionDate BETWEEN '20070901' AND '20080313'
OPTION (QUERYTRACEON 4137);

With this flag active, cardinality estimation uses the minimum selectivity of the two predicates, resulting in an estimate of 68,412.4 rows:

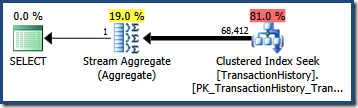
This happens to be just about perfect for our query because our test predicates are exactly correlated (and the estimates derived from the base histograms are also very good).

It is reasonably rare for predicates to be perfectly correlated like this with real data, but the trace flag may nevertheless help in some cases. Note that the minimum selectivity behaviour will apply to all conjunctive (AND) predicates in the query; there is no way to specify the behaviour at a more granular level.

There is no corresponding trace flag to estimate disjunctive (OR) predicates using minimum selectivity.

SQL Server 2014

Selectivity computation in SQL Server 2014 behaves the same as previous versions (and trace flag 4137 works as before) if the database compatibility level is set lower than 120, or if trace flag 9481 is active. Setting the database compatibility level is the official way to use the pre-2014 cardinality estimator in SQL Server 2014. Trace flag 9481 is effective to do the same thing as at the time of writing, and also works with QUERYTRACEON, though it is not documented to do so. There is no way to know what the RTM behaviour of this flag will be.

If the new cardinality estimator is active, SQL Server 2014 uses a different default formula for combining conjunctive and disjunctive predicates. Although undocumented, the selectivity formula for conjunctions has been discovered and documented several times now. The first one I remember seeing is in this Portuguese blog post and the follow-up part two issued a couple of weeks later. To summarize, the 2014 approach to conjunctive predicates is to use exponential backoff: given a table with cardinality C, and predicate selectivities S₁, S₂, S₃ … S_n, where S₁ is the most selective and S_n the least:

Estimate = C * S1 * SQRT(S2) * SQRT(SQRT(S3)) * SQRT(SQRT(SQRT(S4))) …

The estimate is computed the most selective predicate multiplied by the table cardinality, multiplied by the square root of the next most selective predicate, and so on with each new selectivity gaining an additional square root.

Recalling that selectivity is a number between 0 and 1, it is clear that applying a square root moves the number closer to 1. The effect is to take account of all predicates in the final estimate, but to reduce the impact of the less selective predicates exponentially. There is arguably more logic to this idea than under the independency assumption, but it is still a fixed formula – it does not change based on the actual degree of data correlation.

The 2014 cardinality estimator uses an exponential backoff formula for both conjunctive and disjunctive predicates, though the formula used in the disjunctive (OR) case has not yet been documented (officially or otherwise).

SQL Server 2014 Selectivity Trace Flags

Trace flag 4137 (to use minimum selectivity) does not work in SQL Server 2014, if the new cardinality estimator is used when compiling a query. Instead, there is a new trace flag 9471. When this flag is active, minimum selectivity is used to estimate multiple conjunctive and disjunctive predicates. This is a change from the 4137 behaviour, which only affected conjunctive predicates.

Similarly, trace flag 9472 can be specified to assume independence for multiple predicates, as previous versions did. This flag is different from 9481 (to use the pre-2014 cardinality estimator) because under 9472 the new cardinality estimator will still be used, only the selectivity formula for multiple predicates is affected.

Neither 9471 nor 9472 is documented at the time of writing (though they may be at RTM).

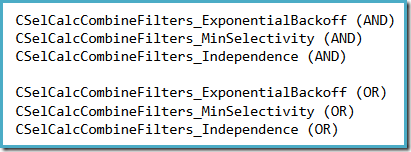
A convenient way to see which selectivity assumption is being used in SQL Server 2014 (with the new cardinality estimator active) is to examine the selectivity computation debug output produced when trace flags 2363 and 3604 are active. The section to look for relates to the selectivity calculator that combines filters, where you will see one of the following, depending on which assumption is being used:

There is no realistic prospect that 2363 will be documented or supported.

Final Thoughts

There is nothing magic about exponential backoff, minimum selectivity, or independence. Each approach represents a (hugely) simplifying assumption that may or may not produce an acceptable estimates for any particular query or data distribution.

In some respects, exponential backoff represents a compromise between the two extremes of independence and minimum selectivity. Even so, it is important not to have unreasonable expectations of it. Until a more accurate way is found to estimate selectivity for multiple predicates (with reasonable performance characteristics) it remains important to be aware of the model limitations and watch out for (potential) estimation errors accordingly.

The various trace flags provide some control over which assumption is used, but the situation is far from perfect. For one thing, the finest granularity at which a flag may be applied is a single query – estimation behaviour cannot be specified at the predicate level. If you have a query where some predicates are correlated and others independent, the trace flags may not help you much without refactoring the query in one way or another. Equally, a problematic query may have predicate correlations that are not modelled well by any of the available options.

Ad-hoc use of the trace flags requires the same permissions as DBCC TRACEON – namely sysadmin. That is probably fine for personal testing, but for production use a plan guide using the QUERYTRACEON hint is a better option. With a plan guide, no additional permissions are required to execute the query (though elevated permissions are required to create the plan guide, of course).