What is the fastest way to calculate the median?

SQL Server has traditionally shied away from providing native solutions to some of the more common statistical questions, such as calculating a median. According to WikiPedia, "median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to highest value and picking the middle one. If there is an even number of observations, then there is no single middle value; the median is then usually defined to be the mean of the two middle values."

In terms of a SQL Server query, the key thing you'll take away from that is that you need to "arrange" (sort) all of the values. Sorting in SQL Server is typically a pretty expensive operation if there isn't a supporting index, and adding an index to support an operation which probably isn't requested that often may not be worthwhile.

Let's examine how we have typically solved this problem in previous versions of SQL Server. First let's create a very simple table so that we can eyeball that our logic is correct and deriving an accurate median. We can test the following two tables, one with an even number of rows, and the other with an odd number of rows:

CREATE TABLE dbo.EvenRows ( id INT PRIMARY KEY, val INT );
CREATE TABLE dbo.OddRows  ( id INT PRIMARY KEY, val INT );

INSERT dbo.EvenRows(id,val) 
          SELECT 1, 6
UNION ALL SELECT 2, 11
UNION ALL SELECT 3, 4
UNION ALL SELECT 4, 4
UNION ALL SELECT 5, 15
UNION ALL SELECT 6, 14
UNION ALL SELECT 7, 4
UNION ALL SELECT 8, 9;

INSERT dbo.OddRows(id,val)
          SELECT 1, 6
UNION ALL SELECT 2, 11
UNION ALL SELECT 3, 4
UNION ALL SELECT 4, 4
UNION ALL SELECT 5, 15
UNION ALL SELECT 6, 14
UNION ALL SELECT 7, 4;

DECLARE @Median DECIMAL(12, 2);

Just from casual observance, we can see that the median for the table with odd rows should be 6, and for the even table it should be 7.5 ((6+9)/2). So now let's see some solutions that have been used over the years:

SQL Server 2000

In SQL Server 2000, we were constrained to a very limited T-SQL dialect. I'm investigating these options for comparison because some people out there are still running SQL Server 2000, and others may have upgraded but, since their median calculations were written "back in the day," the code might still look like this today.

2000_A – max of one half, min of the other

This approach takes the highest value from the first 50 percent, the lowest value from the last 50 percent, then divides them by two. This works for even or odd rows because, in the even case, the two values are the two middle rows, and in the odd case, the two values are actually from the same row.

SELECT @Median = (
   (SELECT MAX(val) FROM
     (SELECT TOP 50 PERCENT val 
      FROM dbo.EvenRows ORDER BY val, id) AS t)
 + (SELECT MIN(val) FROM
     (SELECT TOP 50 PERCENT val 
      FROM dbo.EvenRows ORDER BY val DESC, id DESC) AS b)
) / 2.0;

2000_B – #temp table

This example first creates a #temp table, and using the same type of math as above, determines the two "middle" rows with assistance from a contiguous IDENTITY column ordered by the val column. (The order of assignment of IDENTITY values can only be relied upon because of the MAXDOP setting.)

CREATE TABLE #x
(
  i    INT IDENTITY(1,1),
  val  DECIMAL(12, 2)
);

CREATE CLUSTERED INDEX v ON #x(val);

INSERT #x(val)
  SELECT val 
  FROM dbo.EvenRows
  ORDER BY val OPTION (MAXDOP 1);

SELECT @Median = AVG(val) 
  FROM #x AS x 
  WHERE EXISTS
  (
    SELECT 1 
      FROM #x 
      WHERE x.i - (SELECT  MAX(i) / 2.0 FROM #x) IN (0, 0.5, 1)
  );

SQL Server 2005, 2008, 2008 R2

SQL Server 2005 introduced some interesting new window functions, such as ROW_NUMBER(), which can help solve statistical problems like median a little easier than we could in SQL Server 2000. These approaches all work in SQL Server 2005 and above:

2005_A – dueling row numbers

This example uses ROW_NUMBER() to walk up and down the values once in each direction, then finds the "middle" one or two rows based on that calculation. This is quite similar to the first example above, with easier syntax:

SELECT @Median = AVG(1.0 * val)
FROM
(
   SELECT val, 
      ra = ROW_NUMBER() OVER (ORDER BY val, id),
      rd = ROW_NUMBER() OVER (ORDER BY val DESC, id DESC)
   FROM dbo.EvenRows
) AS x
WHERE ra BETWEEN rd - 1 AND rd + 1;

2005_B – row number + count

This one is quite similar to the above, using a single calculation of ROW_NUMBER() and then using the total COUNT() to find the "middle" one or two rows:

SELECT @Median = AVG(1.0 * Val)
FROM 
(
  SELECT val, 
     c  = COUNT(*) OVER (),
     rn = ROW_NUMBER() OVER (ORDER BY val)
  FROM dbo.EvenRows
) AS x
WHERE rn IN ((c + 1)/2, (c + 2)/2);

2005_C – variation on row number + count

Fellow MVP Itzik Ben-Gan showed me this method, which achieves the same answer as the above two methods, but in a very slightly different way:

SELECT @Median = AVG(1.0 * val)
FROM
(
    SELECT o.val, rn = ROW_NUMBER() OVER (ORDER BY o.val), c.c
    FROM dbo.EvenRows AS o
    CROSS JOIN (SELECT c = COUNT(*) FROM dbo.EvenRows) AS c
) AS x
WHERE rn IN ((c + 1)/2, (c + 2)/2);

SQL Server 2012

In SQL Server 2012, we have new windowing capabilities in T-SQL that allow statistical calculations like median to be expressed more directly. To calculate the median for a set of values, we can use PERCENTILE_CONT(). We can also use the new "paging" extension to the ORDER BY clause (OFFSET / FETCH).

2012_A – new distribution functionality

This solution uses a very straightforward calculation using distribution (if you don't want the average between the two middle values in the case of an even number of rows).

SELECT @Median = PERCENTILE_CONT(0.5) 
  WITHIN GROUP (ORDER BY val) OVER ()
FROM dbo.EvenRows;

2012_B – paging trick

This example implements a clever use of OFFSET / FETCH (and not exactly one for which it was intended) – we simply move to the row that is one before half the count, then take the next one or two rows depending on whether the count was odd or even. Thanks to Itzik Ben-Gan for pointing out this approach.

DECLARE @c BIGINT = (SELECT COUNT(*) FROM dbo.EvenRows);

SELECT AVG(1.0 * val)
FROM (
    SELECT val FROM dbo.EvenRows
     ORDER BY val
     OFFSET (@c - 1) / 2 ROWS
     FETCH NEXT 1 + (1 - @c % 2) ROWS ONLY
) AS x;

But which one performs better?

We've verified that the above methods all produce the expected results on our little table, and we know that the SQL Server 2012 version has the cleanest and most logical syntax. But which one should you be using in your busy production environment? We can build a much bigger table from system metadata, making sure we have plenty of duplicate values. This script will produce a table with 10,000,000 non-unique integers:

USE tempdb;
GO

CREATE TABLE dbo.obj(id INT IDENTITY(1,1), val INT);

CREATE CLUSTERED INDEX x ON dbo.obj(val, id);

INSERT dbo.obj(val) 
SELECT TOP (10000000) o.[object_id]
FROM sys.all_columns AS c 
CROSS JOIN sys.all_objects AS o
CROSS JOIN sys.all_objects AS o2
WHERE o.[object_id] > 0
ORDER BY c.[object_id];

On my system the median for this table should be 146,099,561. I can calculate this pretty quickly without a manual spot check of 10,000,000 rows by using the following query:

SELECT val FROM 
(
    SELECT val, rn = ROW_NUMBER() OVER (ORDER BY val)
    FROM dbo.obj
) AS x 
WHERE rn IN (4999999, 5000000, 5000001);

Results:

val            rn
----           ----
146099561      4999999
146099561      5000000
146099561      5000001

So now we can create a stored procedure for each method, verify that each one produces the correct output, and then measure performance metrics such as duration, CPU and reads. We'll perform all of these steps with the existing table, and also with a copy of the table that does not benefit from the clustered index (we'll drop it and re-create the table as a heap).

I've created seven procedures implementing the query methods above. For brevity I won't list them here, but each one is named dbo.Median_<version>, e.g. dbo.Median_2000_A, dbo.Median_2000_B, etc. corresponding to the approaches described above. If we run these seven procedures using the free SQL Sentry Plan Explorer, here is what we observe in terms of duration, CPU and reads (note that we run DBCC FREEPROCCACHE and DBCC DROPCLEANBUFFERS in between executions):

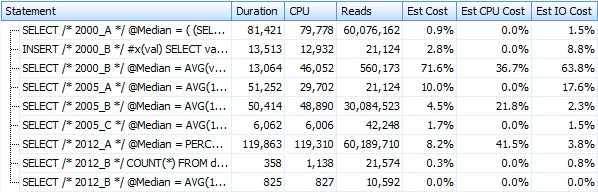
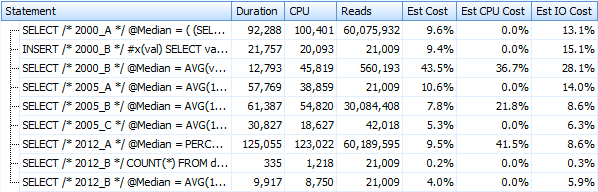
And these metrics don't change much at all if we operate against a heap instead. The biggest percentage change was the method that still ended up being the fastest: the paging trick using OFFSET / FETCH:

Here is a graphical representation of the results. To make it more clear, I highlighted the slowest performer in red and the fastest approach in green.

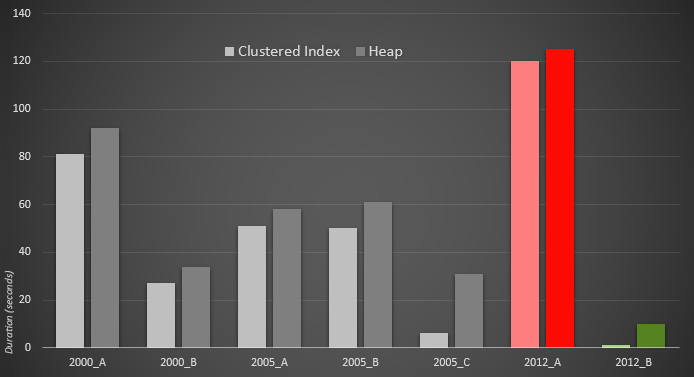
I was surprised to see that, in both cases, PERCENTILE_CONT() – which was designed for this type of calculation – is actually worse than all of the other earlier solutions. I guess it just goes to show that while sometimes newer syntax might make our coding easier, it doesn't always guarantee that performance will improve. I was also surprised to see OFFSET / FETCH prove to be so useful in scenarios that usually wouldn't seem to fit its purpose – pagination.

In any case, I hope I have demonstrated which approach you should use, depending on your version of SQL Server (and that the choice should be the same whether or not you have a supporting index for the calculation).