The Halloween Problem – Part 1

[ Part 1 | Part 2 | Part 3 | Part 4 ]

Much has been written over the years about understanding and optimizing SELECT queries, but rather less about data modification. This series of posts looks at an issue that is specific to INSERT, UPDATE, DELETE and MERGE queries – the Halloween Problem.

The phrase “Halloween Problem” was originally coined with reference to a SQL UPDATE query that was supposed to give a 10% raise to every employee who earned less than $25,000. The problem was that the query kept giving 10% raises until everyone earned at least $25,000. We will see later on in this series that the underlying issue also applies to INSERT, DELETE and MERGE queries, but for this first entry, it will be helpful to examine the UPDATE problem in a bit of detail.

Background

The SQL language provides a way for users to specify database changes using an UPDATE statement, but the syntax says nothing about how the database engine should perform the changes. On the other hand, the SQL standard does specify that the result of an UPDATE must be the same as if it had been executed in three separate and non-overlapping phases:

1. A read-only search determines the records to be changed and the new column values
2. Changes are applied to affected records
3. Database consistency constraints are verified

Implementing these three phases literally in a database engine would produce correct results, but performance might not be very good. The intermediate results at each stage will require system memory, reducing the number of queries the system can execute concurrently. The memory required might also exceed that which is available, requiring at least part of the update set to be written out to disk storage and read back again later on. Last but not least, each row in the table needs to be touched multiple times under this execution model.

An alternative strategy is to process the UPDATE a row at a time. This has the advantage of only touching each row once, and generally does not require memory for storage (though some operations, like a full sort, must process the full input set before producing the first row of output). This iterative model is the one used by the SQL Server query execution engine.

The challenge for the query optimizer is to find an iterative (row by row) execution plan that satisfies the UPDATE semantics required by the SQL standard, while retaining the performance and concurrency benefits of pipelined execution.

Update Processing

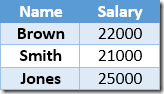
To illustrate the original issue, we will apply a 10% raise to each employee earning less than $25,000 using the Employees table below:

CREATE TABLE dbo.Employees
(
    Name     nvarchar(50) NOT NULL,
    Salary   money NOT NULL
);

INSERT dbo.Employees
    (Name, Salary)
VALUES 
    ('Brown', $22000),
    ('Smith', $21000),
    ('Jones', $25000);

UPDATE e
SET Salary = Salary * $1.1
FROM dbo.Employees AS e
WHERE Salary < $25000;

Three-phase update strategy

The read-only first phase finds all the records that meet the WHERE clause predicate, and saves enough information for the second phase to do its work. In practice, this means recording a unique identifier for each qualifying row (the clustered index keys or heap row identifier) and the new salary value. Once phase one is complete, the whole set of update information is passed to the second phase, which locates each record to be updated using the unique identifier, and changes the salary to the new value. The third phase then checks that no database integrity constraints are violated by the final state of the table.

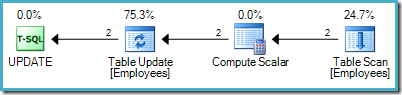
Iterative strategy

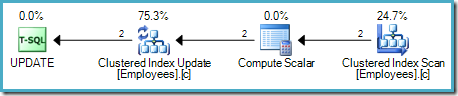
This approach reads one row at a time from the source table. If the row satisfies the WHERE clause predicate, the salary increase is applied. This process repeats until all rows have been processed from the source. A sample execution plan using this model is shown below:

As is usual for SQL Server's demand-driven pipeline, execution starts at the leftmost operator – the UPDATE in this case. It requests a row from the Table Update, which asks for a row from the Compute Scalar, and down the chain to the Table Scan:

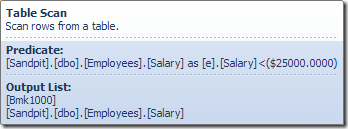
The Table Scan operator reads rows one at a time from the storage engine, until it finds one that satisfies the Salary predicate. The output list in the graphic above shows the Table Scan operator returning a row identifier and the current value of the Salary column for this row. A single row containing references to these two pieces of information is passed up to the Compute Scalar:

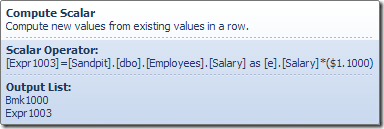
The Compute Scalar defines an expression that applies the salary raise to the current row. It returns a row containing references to the row identifier and the modified salary to the Table Update, which invokes the storage engine to perform the data modification. This iterative process continues until the Table Scan runs out of rows. The same basic process is followed if the table has a clustered index:

The main difference is that the clustered index key(s) and uniquifier (if present) are used as the row identifier instead of a heap RID.

The Problem

Changing from the logical three-phase operation defined in the SQL standard to the physical iterative execution model has introduced a number of subtle changes, only one of which we are going to look at today.  A problem can occur in our running example if there is a nonclustered index on the Salary column, which the query optimizer decides to use to find rows that qualify (Salary < $25,000):

CREATE NONCLUSTERED INDEX nc1
ON dbo.Employees (Salary);

The row-by-row execution model can now produce incorrect results, or even get into an infinite loop. Consider an (imaginary) iterative execution plan that seeks the Salary index, returning a row at a time to the Compute Scalar, and ultimately on to the Update operator:

There are a couple of extra Compute Scalars in this plan due to an optimization that skips nonclustered index maintenance if the Salary value has not changed (only possible for a zero salary in this case).

Ignoring that, the important feature of this plan is that we now have an ordered partial index scan passing a row at a time to an operator that modifies the same index (the green highlight in the SQL Sentry Plan Explorer graphic above makes it clear the Clustered Index Update operator maintains both the base table and the nonclustered index).

Anyway, the problem is that by processing one row at a time, the Update can move the current row ahead of the scan position used by the Index Seek to locate rows to change.  Working through the example should make that statement a bit clearer:

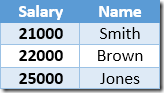
The nonclustered index is keyed, and sorted ascending, on the salary value. The index also contains a pointer to the parent row in the base table (either a heap RID or the clustered index keys plus uniquifier if necessary). To make the example easier to follow, assume the base table now has a unique clustered index on the Name column, so the nonclustered index contents at the start of update processing are:

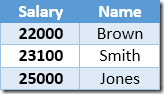
The first row returned by the Index Seek is the $21,000 salary for Smith.  This value is updated to $23,100 in the base table and the nonclustered index by the Clustered Index operator.  The nonclustered index now contains:

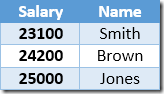
The next row returned by the Index Seek will be the $22,000 entry for Brown which is updated to $24,200:

Now the Index Seek finds the $23,100 value for Smith, which is updated again, to $25,410.  This process continues until all employees have a salary of at least $25,000 – which is not a correct result for the given UPDATE query. The same effect in other circumstances can lead to a runaway update which only terminates when the server runs out of log space or an overflow error occurs (it could occur in this case if someone had a zero salary). This is the Halloween Problem as it applies to updates.

Avoiding the Halloween Problem for Updates

Eagle-eyed readers will have noticed that the estimated cost percentages in the imaginary Index Seek plan did not add up to 100%. This is not a problem with Plan Explorer – I deliberately removed a key operator from the plan:

The query optimizer recognizes that this pipelined update plan is vulnerable to the Halloween Problem, and introduces an Eager Table Spool to prevent it from occurring. There is no hint or trace flag to prevent inclusion of the spool in this execution plan because it is required for correctness.

As its name suggests, the spool eagerly consumes all rows from its child operator (the Index Seek) before returning a row to its parent Compute Scalar. The effect of this is to introduce complete phase separation – all qualifying rows are read and saved into temporary storage before any updates are performed.

This brings us closer to the three-phase logical semantic of the SQL standard, though please note plan execution is still fundamentally iterative, with operators to the right of the spool forming the read cursor, and operators to the left forming the write cursor. The contents of the spool are still read and processed row by row (it is not passed en masse as the comparison with the SQL standard might otherwise lead you to believe).

The drawbacks of the phase separation are the same as mentioned earlier. The Table Spool consumes tempdb space (pages in the buffer pool) and may require physical reads and writes to disk under memory pressure. The query optimizer assigns an estimated cost to the spool (subject to all the usual caveats about estimations) and will choose between plans that require protection against the Halloween Problem versus those that don't on the basis of estimated cost as normal. Naturally, the optimizer may incorrectly choose between the options for any of the normal reasons.

In this case, the trade-off is between the efficiency increase by seeking directly to qualifying records (those with a salary < $25,000) versus the estimated cost of the spool required to avoid the Halloween Problem. An alternative plan (in this specific case) is a full scan of the clustered index (or heap). This strategy does not require the same Halloween Protection because the keys of the clustered index are not modified:

Because the index keys are stable, rows cannot move position in the index between iterations, avoiding the Halloween Problem in the present case. Depending on the runtime cost of the Clustered Index Scan compared with the Index Seek plus Eager Table Spool combination seen previously, one plan may execute faster than the other.  Another consideration is that the plan with Halloween Protection will acquire more locks than the fully pipelined plan, and the locks will be held for longer.

Final Thoughts

Understanding the Halloween Problem and the effects it can have on data modification query plans will help you analyse data-changing execution plans, and can offer opportunities to avoid the costs and side-effects of unnecessary protection where an alternative is available.

There are several forms of the Halloween Problem, not all of which are caused by reading and writing to the keys of a common index. The Halloween Problem is also not limited to UPDATE queries. The query optimizer has more tricks up its sleeve to avoid the Halloween Problem aside from brute-force phase separation using an Eager Table Spool. These points (and more) will be explored in the next installments of this series.

[ Part 1 | Part 2 | Part 3 | Part 4 ]