Back in 2012, I wrote a blog post here highlighting approaches for calculating a median. In that post, I dealt with the very simple case: we wanted to find the median of a column across an entire table. It has been mentioned to me multiple times since then that a more practical requirement is to calculate a partitioned median. Like with the basic case, there are multiple ways to solve this in various versions of SQL Server; not surprisingly, some perform much better than others.
In the previous example, we just had generic columns id and val. Let's make this more realistic and say we have sales people and the number of sales they have made in some period. To test our queries, let's first create a simple heap with 17 rows, and verify that they all produce the results we expect (SalesPerson 1 has a median of 7.5, and SalesPerson 2 has a median of 6.0):
CREATE TABLE dbo.Sales(SalesPerson INT, Amount INT);
GO
INSERT dbo.Sales WITH (TABLOCKX)
(SalesPerson, Amount) VALUES
(1, 6 ),(1, 11),(1, 4 ),(1, 4 ),
(1, 15),(1, 14),(1, 4 ),(1, 9 ),
(2, 6 ),(2, 11),(2, 4 ),(2, 4 ),
(2, 15),(2, 14),(2, 4 );
Here are the queries, which we are going to test (with a lot more data!) against the heap above, as well as with supporting indexes. I've discarded a couple of queries from the previous test, which either didn't scale at all or didn't map very well to partitioned medians (namely, 2000_B, which used a #temp table, and 2005_A, which used opposing row numbers). I have, though, added a few interesting ideas from a recent article by Dwain Camps (@DwainCSQL), which built on my previous post.
SQL Server 2000+
The only method from the previous approach that worked well enough on SQL Server 2000 to even include it in this test was the "min of one half, max of the other" approach:
SELECT DISTINCT s.SalesPerson, Median = (
(SELECT MAX(Amount) FROM
(SELECT TOP 50 PERCENT Amount FROM dbo.Sales
WHERE SalesPerson = s.SalesPerson ORDER BY Amount) AS t)
+ (SELECT MIN(Amount) FROM
(SELECT TOP 50 PERCENT Amount FROM dbo.Sales
WHERE SalesPerson = s.SalesPerson ORDER BY Amount DESC) AS b)
) / 2.0
FROM dbo.Sales AS s;
I did honestly try to mimic the #temp table version that I used in the simpler example, but it did not scale well at all. At 20 or 200 rows it worked fine; at 2000 it took nearly a minute; at 1,000,000 I gave up after an hour. I've included it here for posterity.
CREATE TABLE #x
(
i INT IDENTITY(1,1),
SalesPerson INT,
Amount INT,
i2 INT
);
CREATE CLUSTERED INDEX v ON #x(SalesPerson, Amount);
INSERT #x(SalesPerson, Amount)
SELECT SalesPerson, Amount
FROM dbo.Sales
ORDER BY SalesPerson,Amount OPTION (MAXDOP 1);
UPDATE x SET i2 = i-
(
SELECT COUNT(*) FROM #x WHERE i <= x.i
AND SalesPerson < x.SalesPerson
)
FROM #x AS x;
SELECT SalesPerson, Median = AVG(0. + Amount)
FROM #x AS x
WHERE EXISTS
(
SELECT 1
FROM #x
WHERE SalesPerson = x.SalesPerson
AND x.i2 - (SELECT MAX(i2) / 2.0 FROM #x WHERE SalesPerson = x.SalesPerson)
IN (0, 0.5, 1)
)
GROUP BY SalesPerson;
GO
DROP TABLE #x;
SQL Server 2005+ 1
This uses two different windowing functions to derive a sequence and overall count of amounts per sales person.
SELECT SalesPerson, Median = AVG(1.0*Amount)
FROM
(
SELECT SalesPerson, Amount, rn = ROW_NUMBER() OVER
(PARTITION BY SalesPerson ORDER BY Amount),
c = COUNT(*) OVER (PARTITION BY SalesPerson)
FROM dbo.Sales
)
AS x
WHERE rn IN ((c + 1)/2, (c + 2)/2)
GROUP BY SalesPerson;
SQL Server 2005+ 2
This came from Dwain Camps' article, which does the same as above, in a slightly more elaborate way. This basically unpivots the interesting row(s) in each group.
;WITH Counts AS
(
SELECT SalesPerson, c
FROM
(
SELECT SalesPerson, c1 = (c+1)/2,
c2 = CASE c%2 WHEN 0 THEN 1+c/2 ELSE 0 END
FROM
(
SELECT SalesPerson, c=COUNT(*)
FROM dbo.Sales
GROUP BY SalesPerson
) a
) a
CROSS APPLY (VALUES(c1),(c2)) b(c)
)
SELECT a.SalesPerson, Median=AVG(0.+b.Amount)
FROM
(
SELECT SalesPerson, Amount, rn = ROW_NUMBER() OVER
(PARTITION BY SalesPerson ORDER BY Amount)
FROM dbo.Sales a
) a
CROSS APPLY
(
SELECT Amount FROM Counts b
WHERE a.SalesPerson = b.SalesPerson AND a.rn = b.c
) b
GROUP BY a.SalesPerson;
SQL Server 2005+ 3
This was based on a suggestion from Adam Machanic in the comments on my previous post, and also enhanced by Dwain in his article above.
;WITH Counts AS
(
SELECT SalesPerson, c = COUNT(*)
FROM dbo.Sales
GROUP BY SalesPerson
)
SELECT a.SalesPerson, Median = AVG(0.+Amount)
FROM Counts a
CROSS APPLY
(
SELECT TOP (((a.c - 1) / 2) + (1 + (1 - a.c % 2)))
b.Amount, r = ROW_NUMBER() OVER (ORDER BY b.Amount)
FROM dbo.Sales b
WHERE a.SalesPerson = b.SalesPerson
ORDER BY b.Amount
) p
WHERE r BETWEEN ((a.c - 1) / 2) + 1 AND (((a.c - 1) / 2) + (1 + (1 - a.c % 2)))
GROUP BY a.SalesPerson;
SQL Server 2005+ 4
This is similar to "2005+ 1" above, but instead of using COUNT(*) OVER() to derive the counts, it performs a self-join against an isolated aggregate in a derived table.
SELECT SalesPerson, Median = AVG(1.0 * Amount)
FROM
(
SELECT s.SalesPerson, s.Amount, rn = ROW_NUMBER() OVER
(PARTITION BY s.SalesPerson ORDER BY s.Amount), c.c
FROM dbo.Sales AS s
INNER JOIN
(
SELECT SalesPerson, c = COUNT(*)
FROM dbo.Sales GROUP BY SalesPerson
) AS c
ON s.SalesPerson = c.SalesPerson
) AS x
WHERE rn IN ((c + 1)/2, (c + 2)/2)
GROUP BY SalesPerson;
SQL Server 2012+ 1
This was a very interesting contribution from fellow SQL Server MVP Peter "Peso" Larsson (@SwePeso) in the comments on Dwain's article; it uses CROSS APPLY and the new OFFSET / FETCH functionality in an even more interesting and surprising way than Itzik's solution to the simpler median calculation.
SELECT d.SalesPerson, w.Median
FROM
(
SELECT SalesPerson, COUNT(*) AS y
FROM dbo.Sales
GROUP BY SalesPerson
) AS d
CROSS APPLY
(
SELECT AVG(0E + Amount)
FROM
(
SELECT z.Amount
FROM dbo.Sales AS z
WHERE z.SalesPerson = d.SalesPerson
ORDER BY z.Amount
OFFSET (d.y - 1) / 2 ROWS
FETCH NEXT 2 - d.y % 2 ROWS ONLY
) AS f
) AS w(Median);
SQL Server 2012+ 2
Finally, we have the new PERCENTILE_CONT() function introduced in SQL Server 2012.
SELECT SalesPerson, Median = MAX(Median)
FROM
(
SELECT SalesPerson,Median = PERCENTILE_CONT(0.5) WITHIN GROUP
(ORDER BY Amount) OVER (PARTITION BY SalesPerson)
FROM dbo.Sales
)
AS x
GROUP BY SalesPerson;
The Real Tests
To test the performance of the above queries, we're going to build a much more substantial table. We're going to have 100 unique salespeople, with 10,000 sales amount figures each, for a total of 1,000,000 rows. We're also going to run each query against the heap as it is, with an added non-clustered index on (SalesPerson, Amount), and with a clustered index on the same columns. Here is the setup:
CREATE TABLE dbo.Sales(SalesPerson INT, Amount INT);
GO
--CREATE CLUSTERED INDEX x ON dbo.Sales(SalesPerson, Amount);
--CREATE NONCLUSTERED INDEX x ON dbo.Sales(SalesPerson, Amount);
--DROP INDEX x ON dbo.sales;
;WITH x AS
(
SELECT TOP (100) number FROM master.dbo.spt_values GROUP BY number
)
INSERT dbo.Sales WITH (TABLOCKX) (SalesPerson, Amount)
SELECT x.number, ABS(CHECKSUM(NEWID())) % 99
FROM x CROSS JOIN x AS x2 CROSS JOIN x AS x3;
And here are the results of the above queries, against the heap, the non-clustered index, and the clustered index:
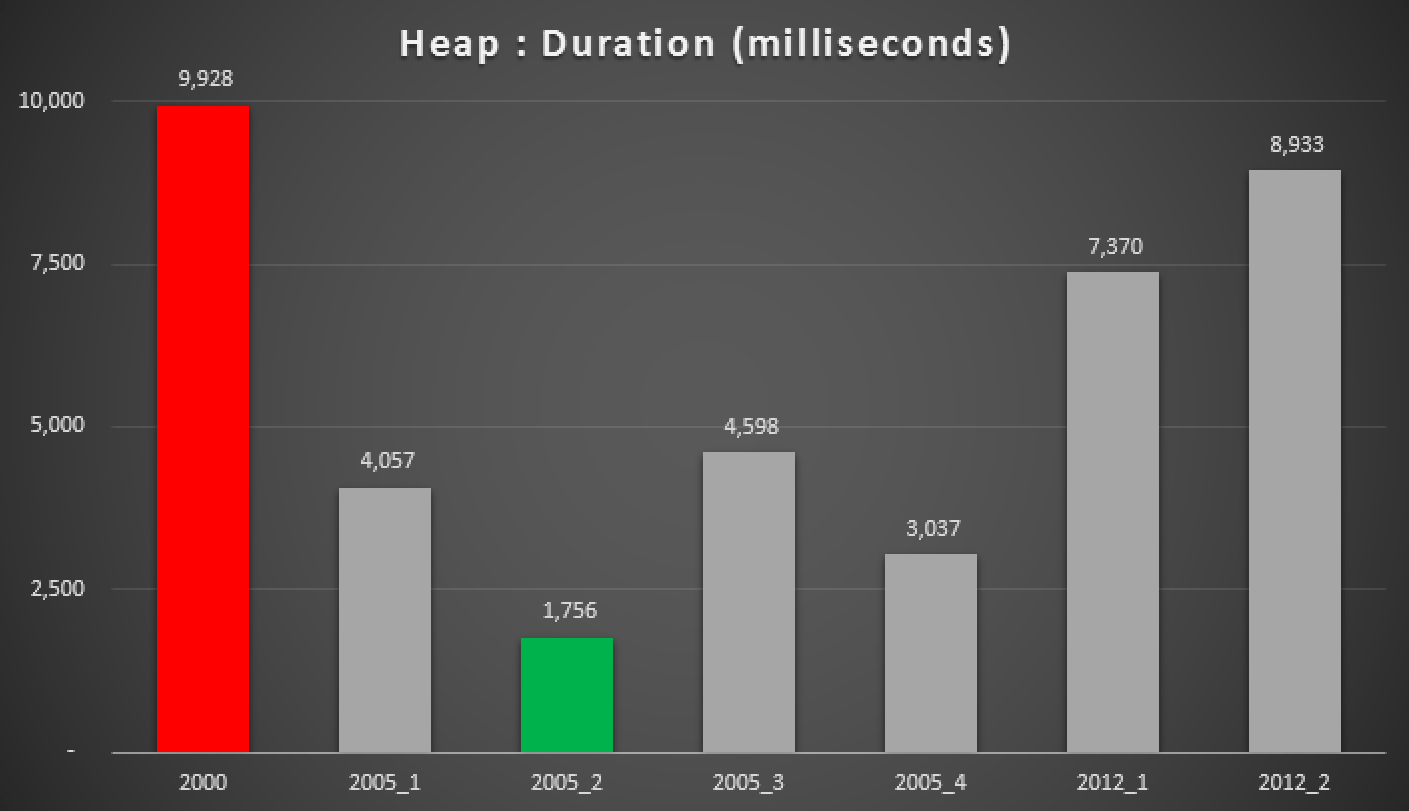
Duration, in milliseconds, of various grouped median approaches (against a heap)
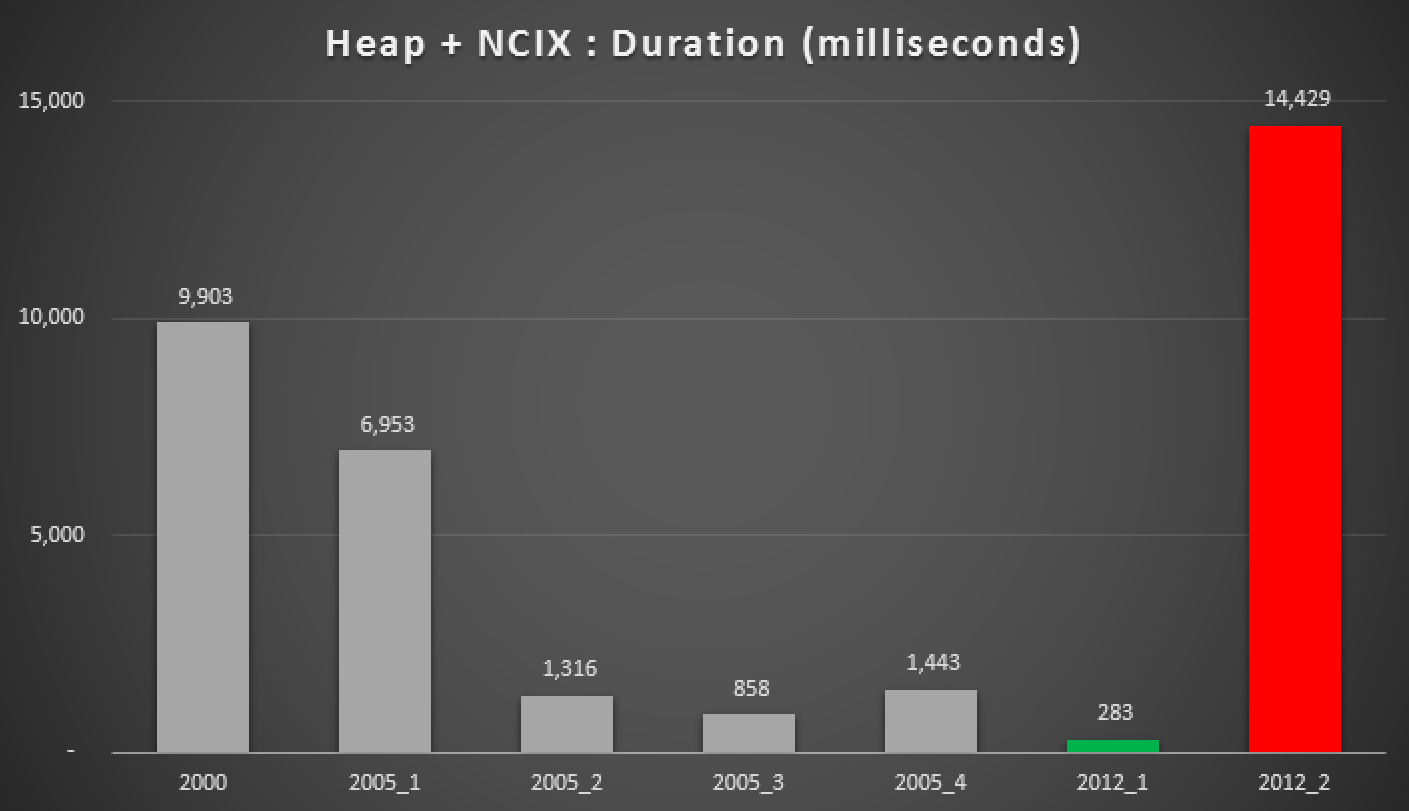
Duration, in milliseconds, of various grouped median approaches (against a heap with a non-clustered index)
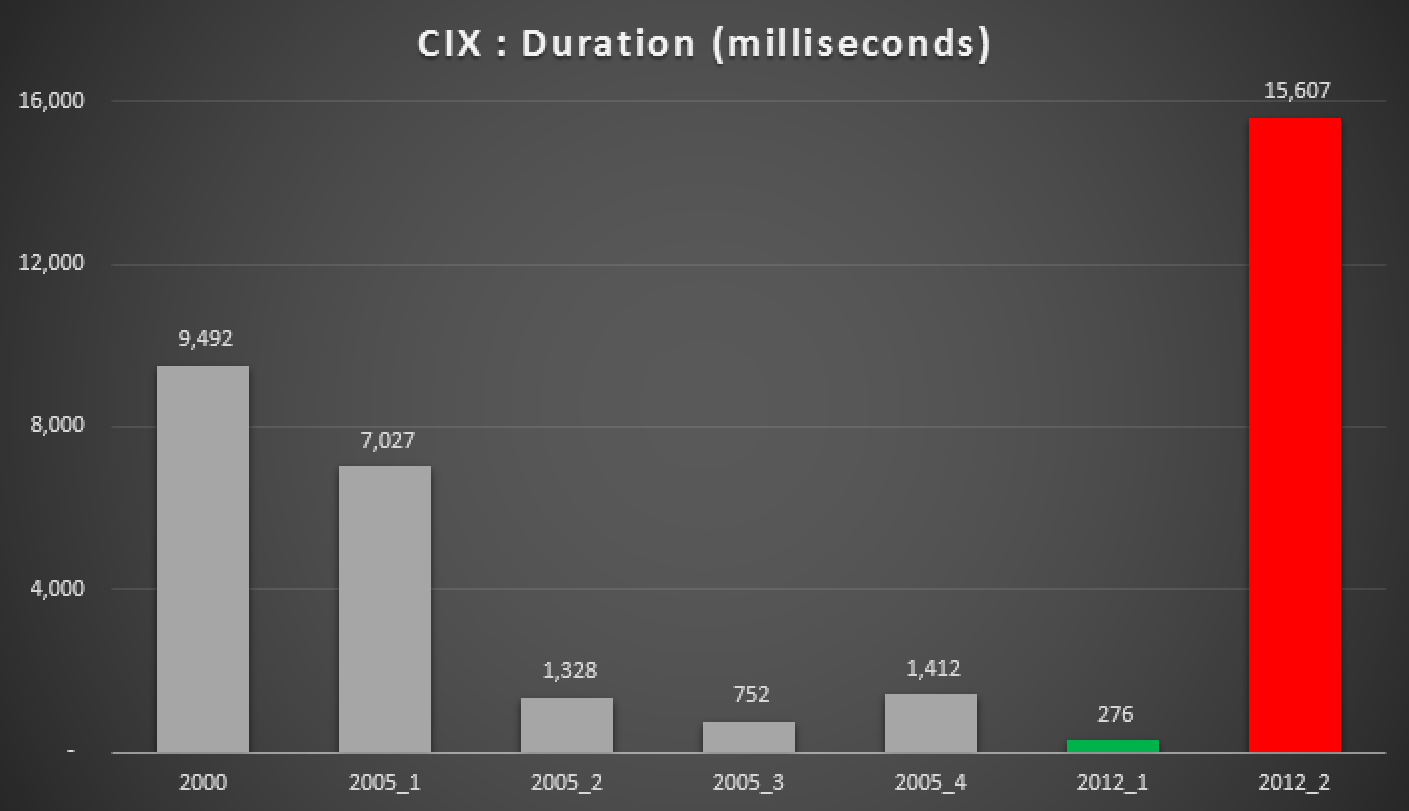
Duration, in milliseconds, of various grouped median approaches (against a clustered index)
What about Hekaton?
Naturally, I was curious if this new feature in SQL Server 2014 could help out with any of these queries. So I created an In-Memory database, two In-Memory versions of the Sales table (one with a hash index on (SalesPerson, Amount), and the other on just (SalesPerson)), and re-ran the same tests:
CREATE DATABASE Hekaton;
GO
ALTER DATABASE Hekaton ADD FILEGROUP xtp CONTAINS MEMORY_OPTIMIZED_DATA;
GO
ALTER DATABASE Hekaton ADD FILE (name = 'xtp', filename = 'c:\temp\hek.mod') TO FILEGROUP xtp;
GO
ALTER DATABASE Hekaton SET MEMORY_OPTIMIZED_ELEVATE_TO_SNAPSHOT ON;
GO
USE Hekaton;
GO
CREATE TABLE dbo.Sales1
(
ID INT IDENTITY(1,1) PRIMARY KEY NONCLUSTERED,
SalesPerson INT NOT NULL,
Amount INT NOT NULL,
INDEX x NONCLUSTERED HASH (SalesPerson, Amount) WITH (BUCKET_COUNT = 256)
)
WITH (MEMORY_OPTIMIZED = ON, DURABILITY = SCHEMA_AND_DATA);
GO
CREATE TABLE dbo.Sales2
(
ID INT IDENTITY(1,1) PRIMARY KEY NONCLUSTERED,
SalesPerson INT NOT NULL,
Amount INT NOT NULL,
INDEX x NONCLUSTERED HASH (SalesPerson) WITH (BUCKET_COUNT = 256)
)
WITH (MEMORY_OPTIMIZED = ON, DURABILITY = SCHEMA_AND_DATA);
GO
;WITH x AS
(
SELECT TOP (100) number FROM master.dbo.spt_values GROUP BY number
)
INSERT dbo.Sales1 (SalesPerson, Amount) -- TABLOCK/TABLOCKX not allowed here
SELECT x.number, ABS(CHECKSUM(NEWID())) % 99
FROM x CROSS JOIN x AS x2 CROSS JOIN x AS x3;
INSERT dbo.Sales2 (SalesPerson, Amount)
SELECT SalesPerson, Amount
FROM dbo.Sales1;
The results:
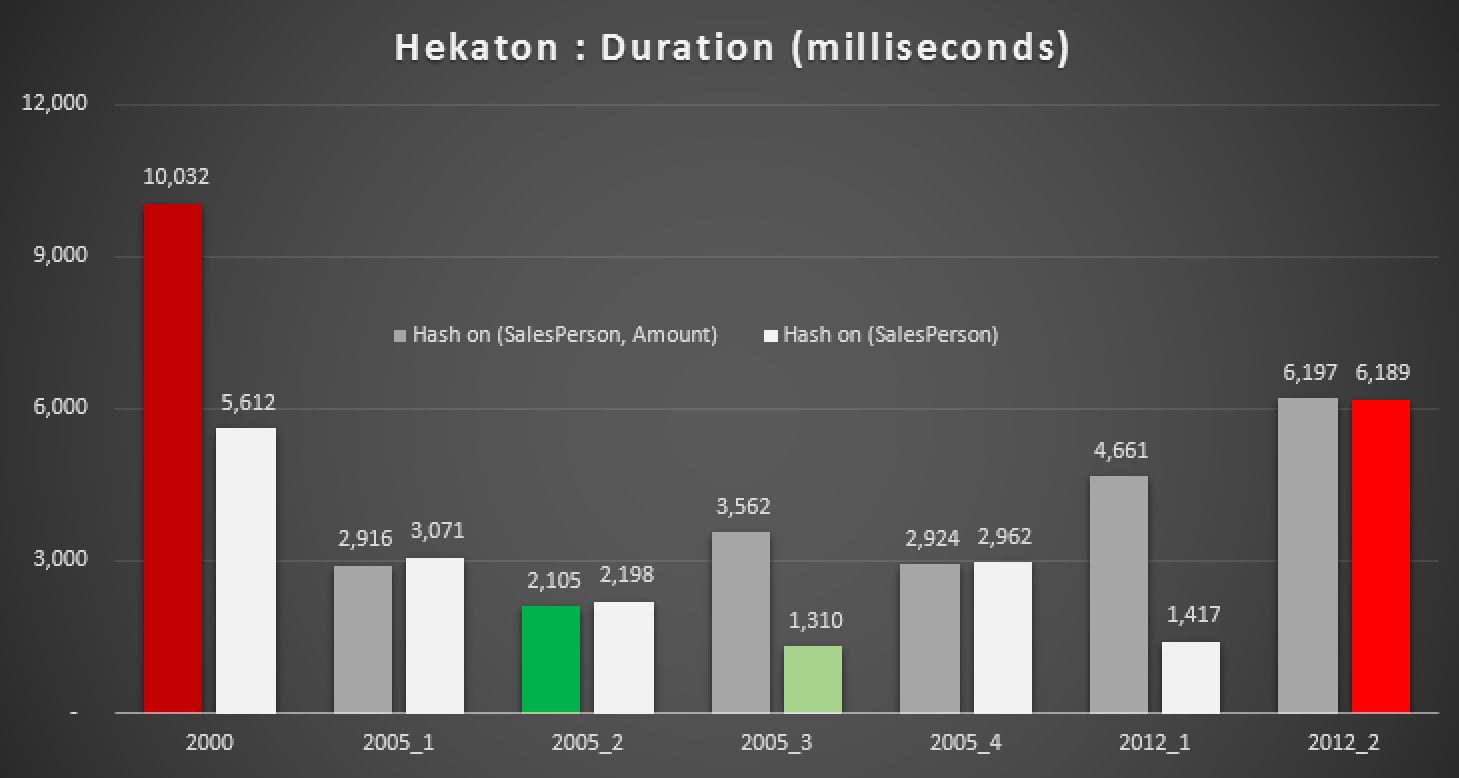
Duration, in milliseconds, for various median calculations against In-Memory tables
Even with the right hash index, we don't really see significant improvements over a traditional table. Further to that, trying to solve the median problem using a natively-compiled stored procedure is not going to be an easy task, as many of the language constructs used above are not valid (I was surprised about a few of these, too). Trying to compile all of the above query variations yielded this parade of errors; some occurred multiple times within each procedure, and even after removing duplicates, this is still kind of comical:
The option 'DISTINCT' is not supported with natively compiled stored procedures.
Msg 12311, Level 16, State 37, Procedure GroupedMedian_2000
Subqueries (queries nested inside another query) are not supported with natively compiled stored procedures.
Msg 10794, Level 16, State 48, Procedure GroupedMedian_2000
The option 'PERCENT' is not supported with natively compiled stored procedures.
Msg 12311, Level 16, State 37, Procedure GroupedMedian_2005_1
Subqueries (queries nested inside another query) are not supported with natively compiled stored procedures.
Msg 10794, Level 16, State 91, Procedure GroupedMedian_2005_1
The aggregate function 'ROW_NUMBER' is not supported with natively compiled stored procedures.
Msg 10794, Level 16, State 56, Procedure GroupedMedian_2005_1
The operator 'IN' is not supported with natively compiled stored procedures.
Msg 12310, Level 16, State 36, Procedure GroupedMedian_2005_2
Common Table Expressions (CTE) are not supported with natively compiled stored procedures.
Msg 12309, Level 16, State 35, Procedure GroupedMedian_2005_2
Statements of the form INSERT...VALUES... that insert multiple rows are not supported with natively compiled stored procedures.
Msg 10794, Level 16, State 53, Procedure GroupedMedian_2005_2
The operator 'APPLY' is not supported with natively compiled stored procedures.
Msg 12311, Level 16, State 37, Procedure GroupedMedian_2005_2
Subqueries (queries nested inside another query) are not supported with natively compiled stored procedures.
Msg 10794, Level 16, State 91, Procedure GroupedMedian_2005_2
The aggregate function 'ROW_NUMBER' is not supported with natively compiled stored procedures.
Msg 12310, Level 16, State 36, Procedure GroupedMedian_2005_3
Common Table Expressions (CTE) are not supported with natively compiled stored procedures.
Msg 12311, Level 16, State 37, Procedure GroupedMedian_2005_3
Subqueries (queries nested inside another query) are not supported with natively compiled stored procedures.
Msg 10794, Level 16, State 91, Procedure GroupedMedian_2005_3
The aggregate function 'ROW_NUMBER' is not supported with natively compiled stored procedures.
Msg 10794, Level 16, State 53, Procedure GroupedMedian_2005_3
The operator 'APPLY' is not supported with natively compiled stored procedures.
Msg 12311, Level 16, State 37, Procedure GroupedMedian_2005_4
Subqueries (queries nested inside another query) are not supported with natively compiled stored procedures.
Msg 10794, Level 16, State 91, Procedure GroupedMedian_2005_4
The aggregate function 'ROW_NUMBER' is not supported with natively compiled stored procedures.
Msg 10794, Level 16, State 56, Procedure GroupedMedian_2005_4
The operator 'IN' is not supported with natively compiled stored procedures.
Msg 12311, Level 16, State 37, Procedure GroupedMedian_2012_1
Subqueries (queries nested inside another query) are not supported with natively compiled stored procedures.
Msg 10794, Level 16, State 38, Procedure GroupedMedian_2012_1
The operator 'OFFSET' is not supported with natively compiled stored procedures.
Msg 10794, Level 16, State 53, Procedure GroupedMedian_2012_1
The operator 'APPLY' is not supported with natively compiled stored procedures.
Msg 12311, Level 16, State 37, Procedure GroupedMedian_2012_2
Subqueries (queries nested inside another query) are not supported with natively compiled stored procedures.
Msg 10794, Level 16, State 90, Procedure GroupedMedian_2012_2
The aggregate function 'PERCENTILE_CONT' is not supported with natively compiled stored procedures.
As currently written, not one of these queries could be ported to a natively-compiled stored procedure. Perhaps something to look into for another follow-up post.
Conclusion
Discarding the Hekaton results, and when a supporting index is present, Peter Larsson's query ("2012+ 1") using OFFSET/FETCH came out as the far-and-away winner in these tests. While a little more complex than the equivalent query in the non-partitioned tests, this matched the results I observed last time.
In those same cases, the 2000 MIN/MAX approach and 2012's PERCENTILE_CONT() came out as real dogs; again, just like my previous tests against the simpler case.
If you are not on SQL Server 2012 yet, then your next best option is "2005+ 3" (if you have a supporting index) or "2005+ 2" if you are dealing with a heap. Sorry I had to come up with a new naming scheme for these, mostly to avoid confusion with the methods in my previous post.
Of course, these are my results against a very specific schema and data set - as with all recommendations, you should test these approaches against your schema and data, as other factors may influence different results.
One other note
In addition to being a poor performer, and not being supported in natively-compiled stored procedures, one other pain point of PERCENTILE_CONT() is that it can't be used in older compatibility modes. If you try, you get this error:
The PERCENTILE_CONT function is not allowed in the current compatibility mode. It is only allowed in 110 mode or higher.








Very nice follow on piece Aaron. Interesting that Hekaton had so many issues. I'm always happy when one of my solution can place amongst the big boys!
Had simpler poor results with Hekaton when we tested it, after spending the time to fit the reporting agg table into the 8k total col length limit.
The real advantage, I guess, remains with Hekaton speeding up inserts.
I wonder how Hekaton tables compare to #tmp tables? Is this a good use case for them?
Any difference when using a ColumnStore index with above?
The table may be too simple to really get any value from the column store index, I guess.
Good article. Can someone help me with a median weight by frequency? For example 3 times price X and 4 times price y. Aggregate of db is price.
Hi Jet,
Can you post more details about your schema, data, and desired results? A good place for a question like this is a community Q & A site, like http://dba.stackexchange.com/
Perhaps there's an even faster solution to calculating the Median on a heap:
http://dwaincsql.com/2015/04/09/an-even-faster-method-of-calculating-the-median-on-a-partitioned-heap/
Interesting article, thanks.
I realise this is an older post now but have you done any work on calculating the quartiles (ie. the mid point of the top and bottom halves)? I find some of these fall apart when I try to move off the median and I was wondering if you had done any work on that.
Thanks
To make it even more useful, how about median by salesperson by date?
Output could be something like:
1/1/2016 fred 6.2
1/1/2016 joe 8.4
1/1/2016 tom 12
1/2/2016 fred 8
1/2/2016 joe 12
1/2/2016 tom 10
etc